Les méthodes de William Gann (Partie III) : L'astrologie fonctionne-t-elle ?

Introduction

Les acteurs des marchés financiers sont constamment à la recherche de nouvelles méthodes d'analyse et de prévision des marchés. Même les concepts les plus incroyables ne sont pas laissés de côté. L'une des approches non standard et tout à fait unique est l'utilisation de l'astrologie dans le trading, qui a été popularisée par le célèbre trader William Gann.

Nous avons déjà abordé les outils de Gann dans nos articles précédents. Voici la première et la deuxième partie. Nous allons maintenant nous concentrer sur l'impact des positions des planètes et des étoiles sur les marchés mondiaux.

Essayons de combiner les technologies les plus modernes et les connaissances anciennes. Nous utiliserons le langage de programmation Python, ainsi que la plateforme MetaTrader 5 pour trouver le lien entre les phénomènes astronomiques et les mouvements de la paire EURUSD. Nous aborderons la partie théorique de l'astrologie dans la finance, et nous nous essayerons à la partie pratique de l'élaboration d'un système de prévision.

Nous étudierons également la collecte et la synchronisation de données astronomiques et financières, nous créerons une matrice de corrélation et nous visualiserons les résultats. 

Base théorique de l'astrologie dans la finance

Je m'intéresse à ce sujet depuis longtemps et je souhaite aujourd'hui partager mes réflexions sur l'influence de l'astrologie sur les marchés financiers. Il s'agit d'un domaine vraiment fascinant, bien que très controversé.

L'idée de base de l'astrologie financière, telle que je la comprends, est que les mouvements des corps célestes sont liés d'une manière ou d'une autre aux cycles du marché. Ce concept a une longue et riche histoire, et a notamment été popularisé par William Gann, un célèbre trader du siècle dernier.

J'ai beaucoup réfléchi aux principes de base de cette théorie. Par exemple, l'idée de cyclicité selon laquelle les mouvements des étoiles et des planètes sont de nature cyclique, tout comme les mouvements du marché. En ce qui concerne les aspects planétaires, certains pensent que certaines positions planétaires ont une forte influence sur les marchés. Qu'en est-il des signes du zodiaque ? On pense que le passage des planètes dans les différentes constellations du zodiaque a également une incidence sur le marché.

Les cycles lunaires et l'activité solaire méritent également d'être mentionnés. J'ai vu des opinions selon lesquelles les phases de la lune sont associées aux fluctuations à court terme du marché, et que les éruptions solaires sont associées aux tendances à long terme. Des hypothèses intéressantes, n'est-ce pas ?

William Gann a été un véritable pionnier dans ce domaine. Il a développé un certain nombre d'outils, comme son célèbre carré de 9, basé sur l'astronomie, la géométrie et les suites de nombres. Ses œuvres suscitent encore de vifs débats.

Bien entendu, on ne peut ignorer que la communauté scientifique dans son ensemble est sceptique à l'égard de l'astrologie. Dans de nombreux pays, elle est officiellement reconnue comme une pseudo-science. Et franchement, il n'y a pas encore de preuve stricte de l'efficacité des méthodes astrologiques dans la finance. Souvent, certaines corrélations observées s'avèrent être simplement le résultat de biais cognitifs.

Malgré cela, de nombreux traders défendent ardemment les idées de l'astrologie financière.

C'est pourquoi j'ai décidé de faire mes propres recherches. Je voudrais essayer de donner une évaluation objective de l'influence de l'astrologie sur les marchés financiers en utilisant des méthodes statistiques et des données massives (big data). Qui sait, peut-être découvrirons-nous quelque chose d'intéressant. Quoi qu'il en soit, ce sera un voyage fascinant dans le monde où les étoiles et les graphiques boursiers se croisent.

Aperçu des bibliothèques Python utilisées

J'aurai besoin de tout un arsenal de bibliothèques Python. 

Pour commencer, j'ai décidé d'utiliser le logiciel Skyfield pour obtenir des données astronomiques. J'ai passé beaucoup de temps à choisir le bon outil, et Skyfield m'a impressionné par sa précision. Grâce à lui, je pourrai collecter des informations sur les positions des corps célestes et les phases de la lune avec une très grande précision à la décimale près - tout ce dont j'ai besoin pour mes ensembles de données.

En ce qui concerne les données de marché, mon choix s'est porté sur la bibliothèque officielle MetaTrader 5 pour Python. Elle permet de télécharger des données historiques sur les paires de devises et même d'ouvrir des transactions si nécessaire.

Pandas deviendra notre fidèle compagnon de travail avec les données. J'ai beaucoup utilisé cette bibliothèque par le passé et elle est tout simplement indispensable pour travailler avec des séries temporelles. Je l'utiliserai pour le prétraitement et la synchronisation de toutes les données collectées.

Pour l'analyse statistique, j'ai opté pour la bibliothèque SciPy. Ses nombreuses fonctionnalités sont impressionnantes, en particulier les outils d'analyse de corrélation et de régression. J'espère qu'elles m'aideront à trouver des modèles intéressants.

Pour visualiser les résultats, j'ai décidé d'utiliser mes bons vieux amis : Matplotlib et Seaborn. J'aime ces bibliothèques pour leur flexibilité dans la création de graphiques. Je suis sûr qu'elles aideront à visualiser tous les résultats.

L'ensemble est assemblé. C'est comme assembler un PC puissant à partir d'excellents composants. Nous disposons désormais de tous les éléments nécessaires pour mener une étude approfondie de l'influence des facteurs astrologiques sur les marchés financiers. J'ai hâte de me plonger dans les données et de commencer à tester mes hypothèses !

Collecte de données astronomiques

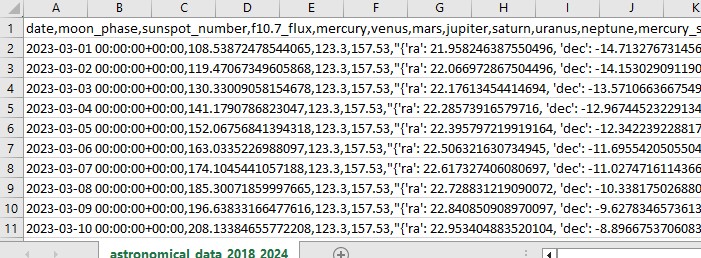
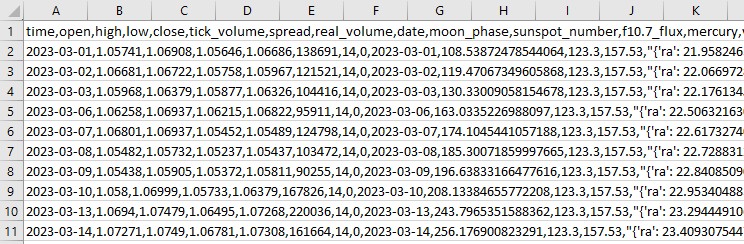
import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests

# Loading planet ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    # Get solar activity data from NOAA API
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    # Convert date to 'YYYY-MM' format
    target_date = date.strftime("%Y-%m")
    
    # Find the closest date in the data
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

start_date = datetime(2024, 4, 1, tzinfo=utc)
end_date = datetime(2024, 5, 31, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)
    
    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame
df = pd.DataFrame(astronomical_data)

# Save data to CSV file
df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Data saved to astronomical_data_2018_2024.csv")

Ce code Python collecte des données astronomiques que nous utiliserons à l'avenir pour l'analyse du marché.

Le code couvre la période allant du 1er janvier 2018 au 31 mai 2024 et recueille une série de données telles que :

• La positions des planètes - Vénus, Mercure, Mars, Jupiter, Saturne, Uranus et Neptune
• Les phases lunaires
• L’activité solaire
• Les aspects planétaires (comment les planètes sont alignées l'une par rapport à l'autre)

Le script comprend l'importation de bibliothèques, la boucle principale et l'enregistrement des données au format Excel. Le code utilise la bibliothèque Skyfield déjà mentionnée pour calculer les positions des planètes, Pandas pour les données, et des requêtes pour obtenir des données sur l'activité solaire.

Les fonctions les plus importantes sont get_planet_positions() pour obtenir les positions des planètes (ascension droite et déclinaison), get_moon_phase() pour trouver la phase lunaire actuelle, get_solar_activity() pour obtenir directement les données sur l'activité solaire à partir de l'API NOAA, et calculate_aspects() pour calculer les aspects - les positions des planètes l'une par rapport à l'autre.

Nous passons en revue chaque jour dans le cadre du cycle et nous recueillons toutes les données. Par conséquent, nous sauvegardons tout dans un fichier Excel pour une utilisation ultérieure. 

Obtenir des données financières via MetaTrader 5

Pour obtenir des données financières, nous utiliserons la bibliothèque MetaTrader 5 pour Python. La bibliothèque nous permettra de télécharger des données financières directement à partir du courtier et de recevoir des séries chronologiques de prix pour n'importe quel instrument. Voici notre code pour le chargement des données historiques : 

import MetaTrader5 as mt5
import pandas as pd
from datetime import datetime

# Connect to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set query parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2018, 1, 1)
end_date = datetime(2024, 12, 31)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
df = pd.DataFrame(rates)
df['time'] = pd.to_datetime(df['time'], unit='s')

# Save data to CSV file
df.to_csv(f'{symbol}_data.csv', index=False)

# Terminate the connection to MetaTrader5
mt5.shutdown()

Le script se connecte au terminal de trading, reçoit les données sur l'EURUSD D1, puis crée un dataframe et l'enregistre dans un fichier CSV unique. 

Synchronisation des données astronomiques et financières

Nous disposons donc de données sur l'astronomie, mais aussi sur l'EURUSD. Nous devons maintenant les synchroniser. Combinons les données par dates afin qu'un seul ensemble de données contienne toutes les informations nécessaires, tant financières qu'astronomiques.

import pandas as pd

# Load data
astro_data = pd.read_csv('astronomical_data_2018_2024.csv')
financial_data = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_data['date'] = pd.to_datetime(astro_data['date'])
financial_data['time'] = pd.to_datetime(financial_data['time'])

# Merge data
merged_data = pd.merge(financial_data, astro_data, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)

Le script charge toutes les données enregistrées, formate les colonnes de date au format datetime et combine les ensembles de données par date. Nous obtenons ainsi un fichier CSV qui contient toutes les données dont nous avons besoin pour nos analyses futures.

Analyse statistique des corrélations

Passons à autre chose. Nous disposons d'un ensemble de données commun, et il est temps de découvrir s'il existe des relations dans les données entre l'astronomie et les mouvements du marché. Nous utiliserons les fonctions corr() de la bibliothèque pandas. Et nous allons aussi combiner nos deux codes en un seul.

Voici le script final :

import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt

# Part 1: Collecting astronomical data

# Loading planetary ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']

    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()

    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()

    target_date = date.strftime("%Y-%m")

    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))

    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees

            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"

    return aspects

# Collecting astronomical data
start_date = datetime(2024, 3, 1, tzinfo=utc)
end_date = datetime(2024, 7, 30, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)

    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)

    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame and save
astro_df = pd.DataFrame(astronomical_data)
astro_df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Astronomical data saved to astronomical_data_2018_2024.csv")

# Part 2: Retrieving financial data via MetaTrader5

# Initialize connection to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set request parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2024, 3, 1)
end_date = datetime(2024, 7, 30)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
financial_df = pd.DataFrame(rates)
financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')

# Save financial data
financial_df.to_csv(f'{symbol}_data.csv', index=False)
print(f"Financial data saved to {symbol}_data.csv")

# Shutdown MetaTrader5 connection
mt5.shutdown()

# Part 3: Synchronizing astronomical and financial data

# Load data
astro_df = pd.read_csv('astronomical_data_2018_2024.csv')
financial_df = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
financial_df['time'] = pd.to_datetime(financial_df['time'])

# Merge data
merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)
print("Merged data saved to merged_astro_financial_data.csv")

# Part 4: Statistical analysis of correlations

# Select numeric columns for correlation analysis
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Create lags for astronomical data
for col in numeric_columns:
    if col not in ['open', 'high', 'low', 'close', 'tick_volume', 'spread', 'real_volume']:
        for lag in range(1, 6):  # Create lags from 1 to 5
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)

# Update list of numeric columns
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Calculate correlation matrix
correlation_matrix = merged_data[numeric_columns].corr()

# Create heatmap of correlations
plt.figure(figsize=(20, 16))
sns.heatmap(correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0)
plt.title('Correlation Matrix of Astronomical Factors (with Lags) and EURUSD Prices')
plt.tight_layout()
plt.savefig('correlation_heatmap_with_lags.png')
plt.close()

# Output the most significant correlations with the closing price
significant_correlations = correlation_matrix['close'].sort_values(key=abs, ascending=False)
print("Most significant correlations with the closing price:")
print(significant_correlations)

# Create a separate correlation matrix for astronomical data with lags and the current price
astro_columns = [col for col in numeric_columns if col not in ['open', 'high', 'low', 'tick_volume', 'spread', 'real_volume']]
astro_columns.append('close')  # Add the current closing price
astro_correlation_matrix = merged_data[astro_columns].corr()

# Create heatmap of correlations for astronomical data with lags and the current price
import seaborn as sns
import matplotlib.pyplot as plt

# Increase the header and axis label font
plt.figure(figsize=(18, 14))
sns.heatmap(astro_correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0, cbar_kws={'label': 'Correlation'})
plt.title('Correlation matrix of astronomical factors (with lags) and current EURUSD price', fontsize=24)
plt.xlabel('X-axis Label', fontsize=30)
plt.ylabel('Y-axis Label', fontsize=30)
plt.xticks(fontsize=30)
plt.yticks(fontsize=30)
plt.tight_layout()
plt.savefig('astro_correlation_heatmap_with_lags.png')
plt.close()

print("Analysis completed. Results saved in CSV and PNG files.")

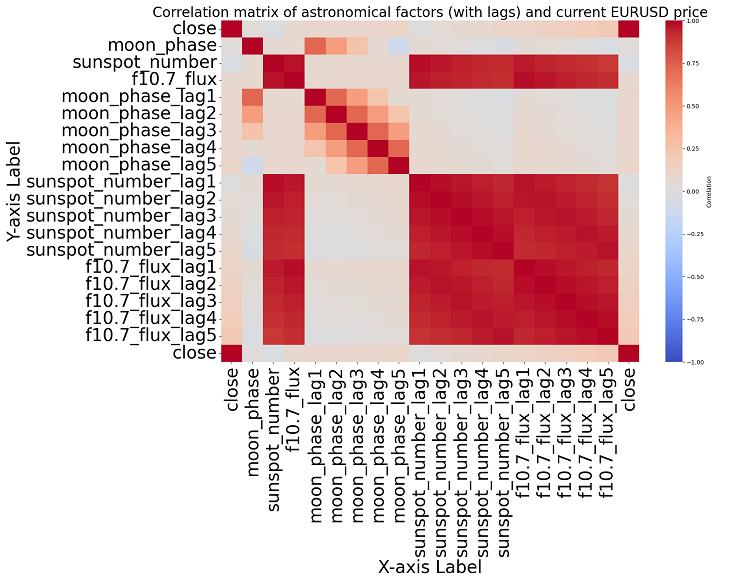
Ce script affiche une carte des corrélations entre tous les nombres de l'ensemble de données, ainsi qu'une matrice de toutes les corrélations au format heatmap, et produit une liste des corrélations les plus significatives avec les prix de clôture.

La présence ou l'absence d'une corrélation n'implique pas la présence ou l'absence d'une relation de cause à effet. Même si nous trouvions de fortes corrélations entre les données astronomiques et les mouvements de prix, cela ne signifierait pas qu'un facteur détermine l'autre, et vice versa. De nouvelles recherches sont nécessaires, car la carte de corrélation n'est que l'élément le plus élémentaire.

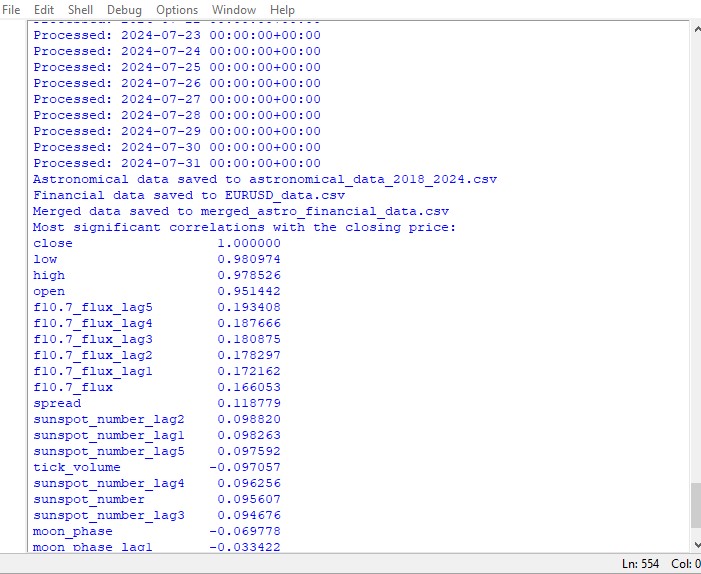
Si nous nous rapprochons du sujet, nous ne parvenons pas à trouver de corrélation significative dans les données. Il n'y a pas de corrélation claire entre les données astronomiques passées et les indicateurs de marché.

L'apprentissage automatique à la rescousse

J'ai réfléchi à la marche à suivre et j'ai décidé d'appliquer un modèle d'apprentissage automatique. J'ai créé 2 scripts utilisant la bibliothèque CatBoost qui tentent de prédire les prix futurs en utilisant les données de l'ensemble de données comme caractéristiques. Voici le premier des modèles - un modèle de régression : 

import pandas as pd
import numpy as np
from catboost import CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder

# Loading data
data = pd.read_csv('merged_astro_financial_data.csv')

# Converting date to datetime
data['date'] = pd.to_datetime(data['date'])

# Creating lags for financial data
for col in ['open', 'high', 'low', 'close']:
    for lag in range(1, 6):  # Creating lags from 1 to 5
        data[f'{col}_lag{lag}'] = data[col].shift(lag)

# Creating lags for astronomical data
astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
for col in astro_cols:
    data[f'{col}_ra'] = data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
    data[f'{col}_dec'] = data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
    for lag in range(1, 6):  # Lags from 1 to 5
        data[f'{col}_ra_lag{lag}'] = data[f'{col}_ra'].shift(lag)
        data[f'{col}_dec_lag{lag}'] = data[f'{col}_dec'].shift(lag)
    data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

# Converting aspects to numerical features
aspect_cols = ['mercury_saturn', 'venus_mars', 'venus_jupiter', 'venus_uranus', 
               'mars_jupiter', 'mars_uranus', 'jupiter_uranus', 'mercury_neptune', 
               'venus_saturn', 'venus_neptune', 'mars_saturn', 'mercury_venus', 
               'mars_neptune', 'mercury_uranus', 'saturn_neptune', 'mercury_jupiter', 
               'mercury_mars', 'jupiter_saturn']

# Using LabelEncoder for encoding aspects
label_encoders = {}
for col in aspect_cols:
    label_encoders[col] = LabelEncoder()
    data[col] = label_encoders[col].fit_transform(data[col].astype(str))

# Filling missing values with mean values for numeric columns
numeric_cols = data.select_dtypes(include=[np.number]).columns
data[numeric_cols] = data[numeric_cols].fillna(data[numeric_cols].mean())

# Removing rows with missing values
data = data.dropna()

# Preparing features and target variable
features = [col for col in data.columns if col not in ['date', 'time', 'close']]
X = data[features]
y = data['close']

# Splitting data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

# Creating and training the CatBoost model
model = CatBoostRegressor(iterations=500, learning_rate=0.1, depth=9, random_state=1)
model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

# Evaluating the model
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
print(f"Mean Absolute Error: {mae}")
print(f"R-squared Score: {r2}")

# Visualizing feature importance
feature_importance = model.feature_importances_
feature_names = X.columns
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
plt.figure(figsize=(12, 6))
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(feature_names)[sorted_idx])
plt.xlabel('Feature Importance')
plt.title('Feature Importance')
plt.show()

# Predicting the next value
def predict_next():
    # Selecting the last row of data
    last_data = data.iloc[-1]
    input_features = last_data[features].values.reshape(1, -1)
    # Prediction
    prediction = model.predict(input_features)
    print(f"Prediction for the next closing price: {prediction[0]}")

# Example of using the function to predict the next value
predict_next()

Le deuxième modèle est la classification :

import pandas as pd
import numpy as np
from skyfield.api import load, utc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.preprocessing import LabelEncoder

# Part 1: Collecting astronomical data

planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    target_date = date.strftime("%Y-%m")
    
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

# Part 2: Obtaining financial data through MetaTrader5

def get_financial_data(symbol, start_date, end_date):
    if not mt5.initialize():
        print("initialize() failed")
        mt5.shutdown()
        return None

    timeframe = mt5.TIMEFRAME_D1

    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    mt5.shutdown()

    financial_df = pd.DataFrame(rates)
    financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')
    return financial_df

# Part 3: Synchronizing astronomical and financial data

def sync_data(astro_df, financial_df):
    astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
    financial_df['time'] = pd.to_datetime(financial_df['time'])
    merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')
    return merged_data

# Part 4: Training the model and making predictions

def train_and_predict(merged_data):
    # Converting aspects to numerical features
    aspect_cols = [col for col in merged_data.columns if '_' in col and col not in ['date', 'time']]
    label_encoders = {}
    for col in aspect_cols:
        label_encoders[col] = LabelEncoder()
        merged_data[col] = label_encoders[col].fit_transform(merged_data[col].astype(str))
    
    # Creating lags for financial data
    for col in ['open', 'high', 'low', 'close']:
        for lag in range(1, 6):
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)
    
    # Creating lags for astronomical data
    astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
    for col in astro_cols:
        merged_data[f'{col}_ra'] = merged_data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
        merged_data[f'{col}_dec'] = merged_data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
        for lag in range(1, 6):
            merged_data[f'{col}_ra_lag{lag}'] = merged_data[f'{col}_ra'].shift(lag)
            merged_data[f'{col}_dec_lag{lag}'] = merged_data[f'{col}_dec'].shift(lag)
        merged_data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

    # Filling missing values with mean values for numeric columns
    numeric_cols = merged_data.select_dtypes(include=[np.number]).columns
    merged_data[numeric_cols] = merged_data[numeric_cols].fillna(merged_data[numeric_cols].mean())

    merged_data = merged_data.dropna()

    # Creating binary target variable
    merged_data['price_change'] = (merged_data['close'].shift(-1) > merged_data['close']).astype(int)

    # Removing rows with missing values in the target variable
    merged_data = merged_data.dropna(subset=['price_change'])

    features = [col for col in merged_data.columns if col not in ['date', 'time', 'close', 'price_change']]
    X = merged_data[features]
    y = merged_data['price_change']

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

    model = CatBoostClassifier(iterations=500, learning_rate=0.1, depth=9, random_state=1)
    model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    clf_report = classification_report(y_test, y_pred)
    conf_matrix = confusion_matrix(y_test, y_pred)

    print(f"Accuracy: {accuracy}")
    print("Classification Report:")
    print(clf_report)
    print("Confusion Matrix:")
    print(conf_matrix)

    # Visualizing feature importance
    feature_importance = model.feature_importances_
    feature_names = X.columns
    sorted_idx = np.argsort(feature_importance)
    pos = np.arange(sorted_idx.shape[0]) + 0.5

    plt.figure(figsize=(12, 6))
    plt.barh(pos, feature_importance[sorted_idx], align='center')
    plt.yticks(pos, np.array(feature_names)[sorted_idx])
    plt.xlabel('Feature Importance')
    plt.title('Feature Importance')
    plt.show()

    # Predicting the next value
    def predict_next():
        last_data = merged_data.iloc[-1]
        input_features = last_data[features].values.reshape(1, -1)
        prediction = model.predict(input_features)
        print(f"Price change prediction (0: will decrease, 1: will increase): {prediction[0]}")

    predict_next()

# Main program
start_date = datetime(2023, 3, 1)
end_date = datetime(2024, 7, 30)

astro_data = []
current_date = start_date

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    astro_data.append({
        'date': current_date,
        'mercury': str(planet_positions['mercury']),
        'venus': str(planet_positions['venus']),
        'mars': str(planet_positions['mars']),
        'jupiter': str(planet_positions['jupiter']),
        'saturn': str(planet_positions['saturn']),
        'uranus': str(planet_positions['uranus']),
        'neptune': str(planet_positions['neptune']),
        'moon_phase': moon_phase,
        **solar_activity,
        **aspects
    })
    
    current_date += timedelta(days=1)

astro_df = pd.DataFrame(astro_data)

symbol = "EURUSD"
financial_data = get_financial_data(symbol, start_date, end_date)

if financial_data is not None:
    merged_data = sync_data(astro_df, financial_data)
    train_and_predict(merged_data)

Malheureusement, aucun des deux modèles n'est très précis. La précision de la classification est légèrement supérieure à 50%, ce qui signifie que nous pouvons tout aussi bien faire une prédiction sur la base d'un tirage au sort.

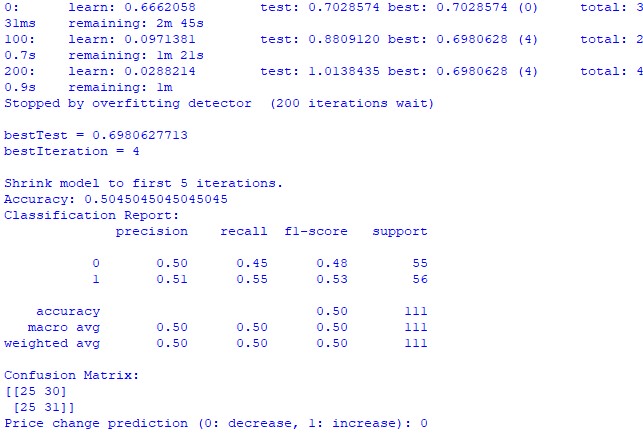
Le résultat peut peut-être être amélioré, étant donné que le modèle de régression a été peu pris en compte et qu'il est possible de prédire les prix en utilisant les positions planétaires et l'activité de la Lune et du Soleil. Je ferai un autre article sur ce sujet si je suis d'humeur à le faire.

Résultats

Il est donc temps de faire la synthèse des résultats. Après avoir effectué une analyse simple et rédigé 2 modèles de prévision, nous voyons les résultats de l'étude sur l'impact potentiel de l'astrologie sur le marché. 

Analyse de corrélation. La carte de corrélation que nous avons obtenue n'a pas révélé de forte corrélation entre les positions planétaires et le cours de clôture de l'EURUSD. Toutes nos corrélations sont inférieures à 0,3, ce qui nous permet de penser que la position des étoiles ou des planètes n'est pas du tout liée aux marchés financiers.

Modèle de régression CatBoost. Les résultats finaux du modèle de régression ont montré une très faible capacité à prédire avec précision les prix de clôture futurs sur la base de données astronomiques.

Les mesures de performance du modèle qui en résultent, telles que MSE, MAE et R au carré, sont très faibles et expliquent très mal les données. Dans le même temps, le modèle montre que les caractéristiques les plus importantes sont les décalages et les valeurs de prix antérieures, plutôt que les positions sur la planète. Cela signifie-t-il que le prix est un meilleur indicateur que la position de n'importe quelle planète de notre système solaire ?

Modèle de classification CatBoost. Le modèle de classification est très peu efficace pour prédire les hausses ou les baisses de prix à venir. La précision dépasse à peine 50%, ce qui confirme également que l'astronomie ne fonctionne pas sur le marché réel.

Conclusion

Les résultats de l'étude sont clairs : les méthodes de l'astrologie et les tentatives de prévision des prix sur le marché réel basées sur des données astronomiques sont totalement inutiles. Je reviendrai peut-être sur ce sujet, mais pour l'instant, les enseignements de William Gann ressemblent à des tentatives de dissimuler des solutions inefficaces créées uniquement pour vendre des livres et des cours de trading.

Se pourrait-il qu'un modèle amélioré utilisant également les valeurs de l'angle de Gann, le carré de 9 et les valeurs de la grille de Gann soit plus performant ? Nous ne le savons pas encore. Je suis un peu déçu par les résultats de l'étude.

Mais je continue à penser que les angles de Gann peuvent être utilisés d'une manière ou d'une autre pour obtenir des prévisions de prix qui fonctionnent. Le prix affecte les angles d'une manière ou d'une autre, il y réagit, comme le montrent les résultats de l'étude précédente. Il est également possible que les angles soient utilisés comme caractéristiques de travail pour les modèles de formation. Je vais essayer de créer un tel ensemble de données et voir ce que cela donne.