I am thrilled to introduce to you my advisor, Phoenix Rig EA, along with comprehensive details about its trading capabilities and system components. Prepare to be amazed by its exquisite performance and remarkable features.
Real Signal: https://www.mql5.com/en/signals/1991005
Important information about the inner workings of an advisor :
I am pleased to share with you an exciting breakthrough in my advisor's trading strategy - the integration of correlation matrices. This innovative addition has yielded remarkable results in both live trading and testing, without falling victim to the common pitfall of excessive optimization. Correlation matrices have long been recognized as a powerful tool in financial analysis, offering insights into the relationships between different assets. By incorporating these matrices into my advisor's framework, I have unlocked a new dimension of market understanding and enhanced its decision-making capabilities. The correlation matrices provide my advisor with a comprehensive overview of the interdependencies amongvarious currency pairs, commodities, or other assets. This information is invaluable when it comes to identifying potential trading opportunities and managing risk effectively. One of the key advantages of utilizing correlation matrices is the ability to diversify trading strategies. By considering the correlations between different assets, my advisor can dynamically adjust its positions to capitalize on market movements while minimizing exposure to correlated risks. This approach helps to reduce drawdowns and enhance overall portfolio stability.Moreover, correlation matrices enable my advisor to optimize its trading decisions based on the strength and direction of correlations. For example, when multiple currency pairs exhibit strong positive or negative correlations, my advisor can make informed decisions to capitalize on these trends or hedge against potential reversals.
What sets my implementation of correlation matrices apart is the emphasis on avoiding over-optimization. Many traders fall into the trap of excessively tuning their strategies based on historical data, which often leads to poor performance in real trading conditions. In contrast, I have taken a prudent approach by utilizing correlation matrices as a supplementary tool rather than relying solely on them. This ensures that my advisor remains adaptable and responsive to changing market dynamics.
The results speak for themselves - my advisor's performance with the integration of correlation matrices has been consistently outstanding. By incorporating this advanced analytical tool into its decision-making process, my advisor has achieved a balance between agility and reliability, resulting in impressive profitability and reduced risk. In conclusion, the successful integration of correlation matrices into my advisor has revolutionized its trading approach. The use of these matrices has provided a deeper understanding of market interdependencies, enabling my advisor to make more informed and strategic trading decisions. The remarkable results obtained, both in real trading and rigorous testing, reaffirm the effectiveness of this enhancement.
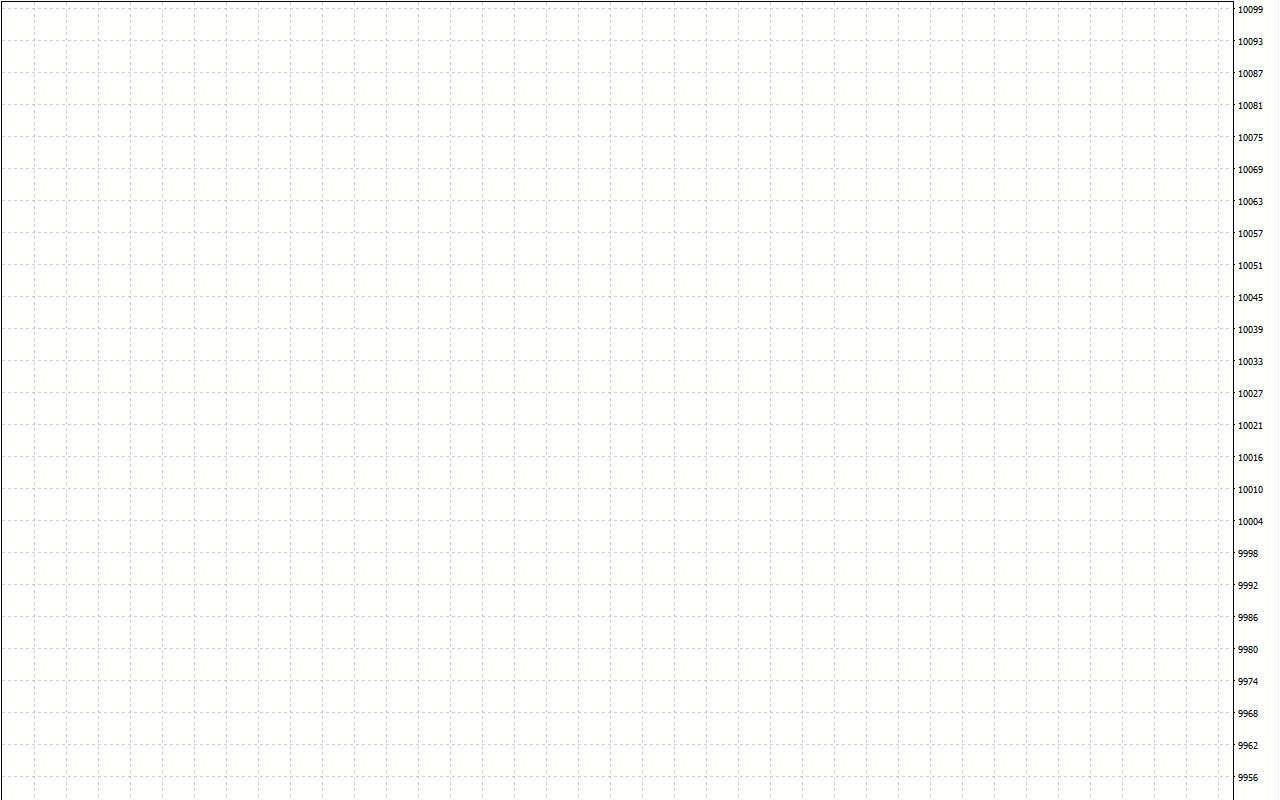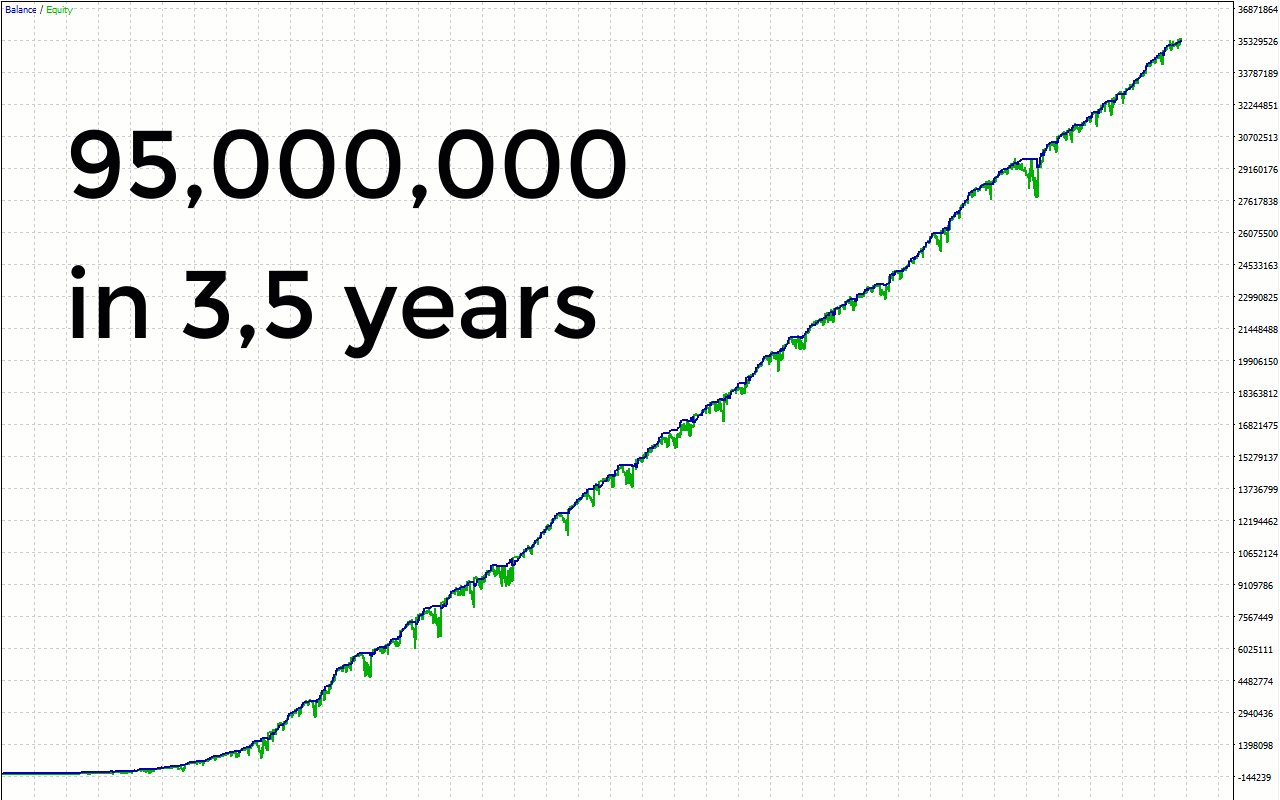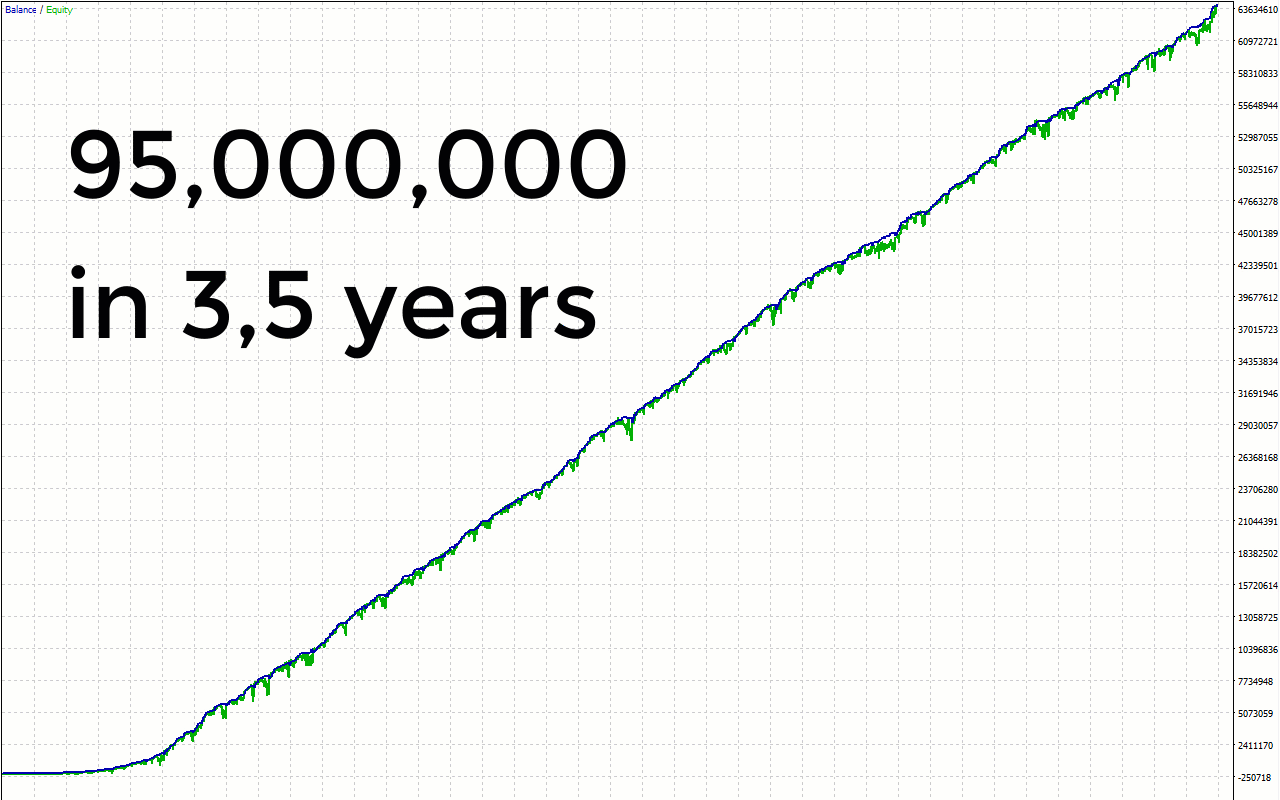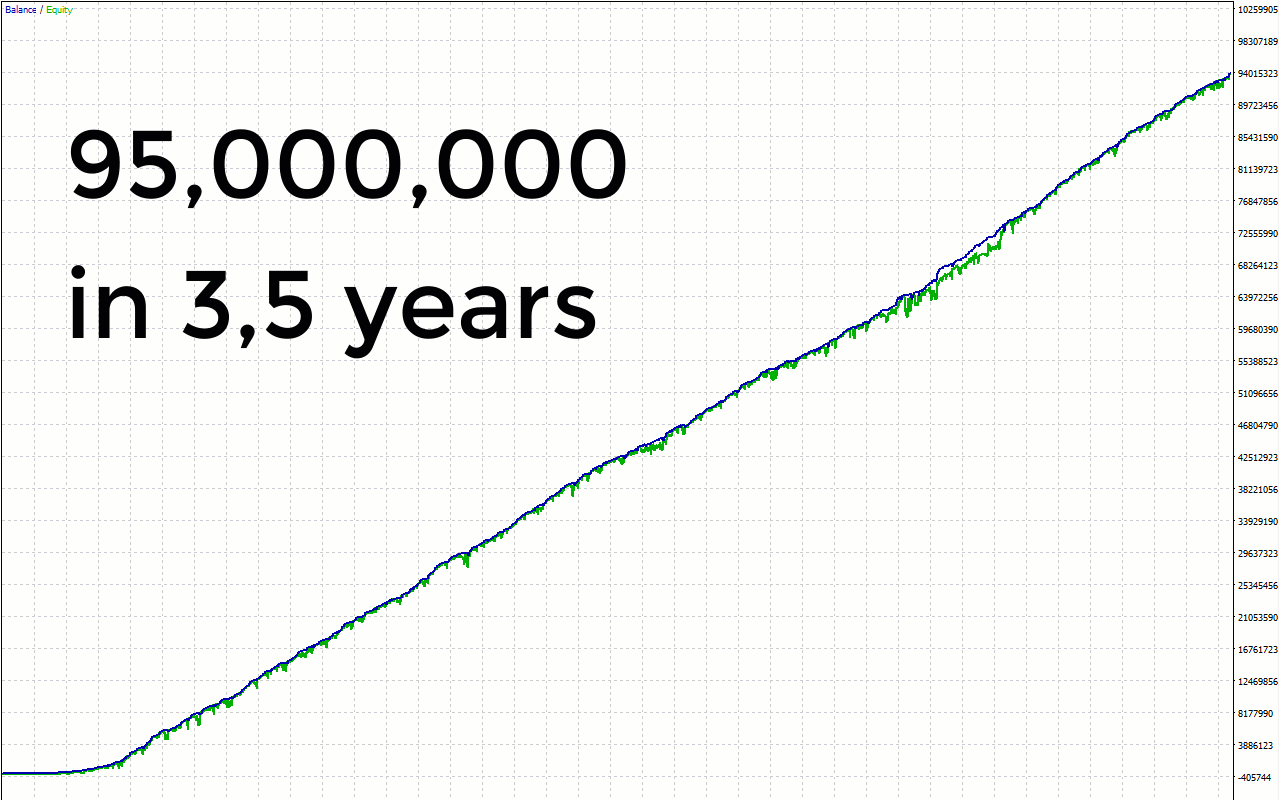
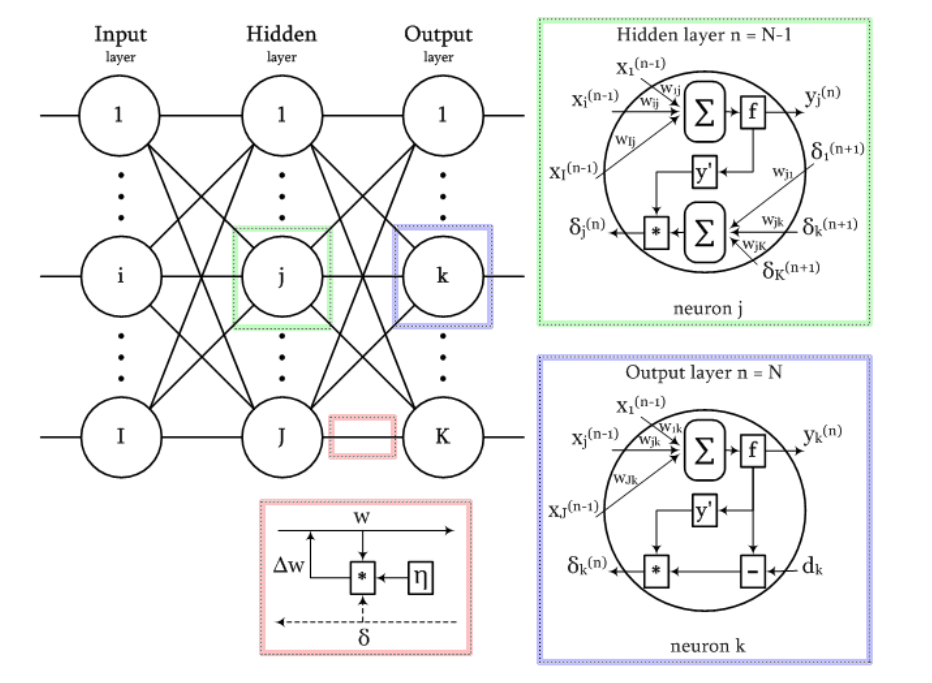
A diagram of the signals in the network when learning the back propagation algorithm is shown in the following figure:
All training images are alternately presented to the input of the network, so that it does not, figuratively speaking, forget some as it remembers others. Usually this is done in random order, but because our data will be placed in matrices and computed as a whole as a single set, in our implementation we will introduce another element of randomness.
The use of matrices means that the weights of all layers, as well as the input and target training data, will be represented by matrices, and the above formulas, and thus the algorithms, will take a matrix form. In other words, we will not be able to operate with separate vectors of input and training data, and the entire cycle from steps 2 to 7 will be calculated for the entire data set at once. One such cycle is called a learning epoch.
Implementing a neural network in a MatrixNet class:
Let's start writing a class of neural network based on MQL5 matrices. Since the network consists of layers, let's describe arrays of weights and output values of neurons of each layer. The number of layers will be stored in the variable n, and weights of neurons in layers and outputs of each layer - in matrices weights and outputs, respectively. Note that the term outputs refers to signals at the outputs of neurons in any layer, not only at the output of the network. So outputs[i] describe both intermediate layers, and even layer 0, where the inputs are fed.The indexing of weights and outputs arrays is illustrated by the following scheme (connections of each neuron with the +1 bias source are not shown for simplicity): 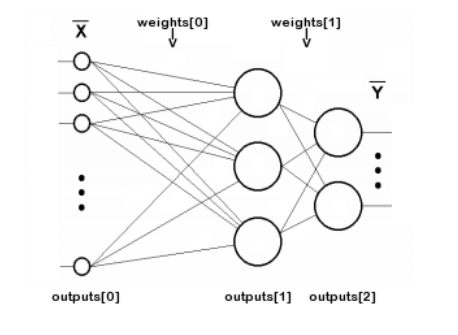
The number n does not include the input layer because it does not require weights.

Training of NS is performed on the training data available at the moment. Based on this data the network configuration (number of layers, number of neurons per layers, etc.), learning rate and other characteristics are chosen. Therefore, in principle, it is always possible to design a network powerful enough to give any sufficiently small error on training data. However, the main strength of NS and the purpose of using NS is that it works well on future unknown data (with the same implicit dependencies as the training set). The effect when a trained NS adjusts too well to the training data, but fails the "forward test" is called overtraining, and should be eradicated in every possible way. For this purpose, the so-called regularization is used - adding some additional conditions to the model or training method that evaluate the generalization ability of the network. There are many different ways of regularization, in particular: analyzing the performance of the trained network on an additional validation dataset (different from the training one); randomly discarding of part of neurons or connections during training; pruning the network after the training; introducing noise into the input data; Artificial data multiplication; Weak constant reduction of the amplitude of weights during training; experimental selection of the volume and configuration of the network on a fine-grained edge, when the network is still capable of learning but no longer retrains on the available data; We implement some of these in our class. To begin with, we will provide for passing not only input and output training data (data and target parameters, respectively), but also a validation set (it also consists of input and paired output vectors: validation and check) to the training method. As the training progresses, network error on training data, as a rule, decreases monotonically enough (the phrase "as a rule" is used, because if the wrong choice of training speed or network capacity is made, the process can go unstable). However, if we count the network error on the validation set in parallel, it will also decrease at first (while the network identifies the most important regularities in the data), and then it will start to grow as it overtrains (when the network adapts already to the specific features of the training sample, but not the validation sample). Thus, the learning process should be stopped when the validation error begins to grow. This approach is called "early stopping". In addition to the two data sets, the train method allows us to set the maximum number of epochs (epochs), the desired accuracy (i.e., the average minimum error, which is enough for us: in this case, training also ends with a success sign), and the method of error calculation (lf). The training speed is set equal to the accuracy, but in order to increase the flexibility of the settings, they can be separated if necessary. This is done because further on we will support automatic speed adjustment, and the initial approximate value is not so important.
First of all, we check that the error value is a valid number. Otherwise there is an overflow in the network or invalid data is fed to the input.
If the error continues to decrease or, at least, does not increase, remember the new error values for comparison in the next epoch. If the error reaches the required accuracy, we consider the training completed and also exit the cycle.
In addition, the loop calls a virtual progress method, which can be overridden in derived network classes, and with it interrupt learning in response to some user action. I will show the standard implementation of progress below.
Finally, if the loop was not interrupted by any of the above conditions, run a backProp of the network error.
The default progress method logs the training values once per second.
The return value true continues learning, while false will cause the loop to terminate. In addition to "early stop", the MatrixNet class knows how to randomly "dropout" some connections a la "dropout". The canonical method of "dropout" involves temporarily excluding randomly selected neurons from the network. However, we cannot implement this without large overhead, because the algorithm uses matrix operations. To exclude neurons from the layer, we would need to reformat the weight matrices and partially copy them at each iteration. It is much easier and more efficient to set random weights to 0, i.e. to break connections. Of course, at the beginning of each epoch, the program should restore temporarily disconnected weights to their previous state, and then select some new ones to disconnect in the next epoch. The number of ties that are temporarily zeroed is set using the enableDropOut method as a percentage of the total number of weights in the network. By default, the dropOutRate variable is 0, and the mode is disabled.
The principle of "dropout" consists in saving the current state of weight matrices in some additional storage (the DropOutState class implements it) and zeroing out randomly chosen connections of the network. After training the network in the obtained modified form for one epoch, the zeroed matrix elements are restored from the storage, and the procedure is repeated: other random weights are selected and zeroed, the network is trained with them, and so on.
I am thrilled to share with you an incredible breakthrough achieved through the implementation of a Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) in my trading advisor. This revolutionary combination has enabled me to uncover patterns and achieve outstanding results, leading to consistent profitability without excessive optimization. This highlights a stark contrast to other users who heavily optimize their advisors solely based on historical data, resulting in favorable backtesting results but poor real-world performance. However, through my meticulous efforts, I have discovered a secret methodology that delivers exceptional outcomes in both backtesting and live trading on real accounts, which have been running successfully for an extended period.
- The integration of CNN and LSTM within my trading advisor has unlocked unprecedented potential. The CNN component excels in extracting meaningful features and identifying visual patterns from market data, allowing for enhanced market understanding and improved decision-making. On the other hand, LSTM, with its ability to retain long-term dependencies, captures sequential patterns and temporal dynamics in the data, providing valuable insights into trends and price movements.
- By leveraging the power of CNN and LSTM, my advisor transcends the limitations of traditional trading strategies. It can identify complex relationships and correlations within the market, adapt to changing conditions, and generate highly accurate predictions of future price movements. This remarkable predictive capability allows for precise entry and exit points, maximizing profitability while effectively managing risk.
- One crucial aspect that distinguishes my approach is the emphasis on avoiding excessive optimization. While many traders fall into the trap of overfitting their strategies to historical data, I have taken a more cautious approach, striving to strike a balance between historical performance and robustness in real-world trading conditions. This ensures that my advisor remains versatile and resilient, capable of adapting to evolving market dynamics.
- The exceptional results achieved by my advisor serve as a testament to the effectiveness of this unique methodology. Through tireless dedication and meticulous refinement, I have harnessed the power of CNN and LSTM to unlock hidden trading opportunities and consistently generate profits. The methodology has proven its merit in both backtesting and live trading, providing a strong foundation for long-term success.
A little secret about the advisor..
Allow me to share a discreet facet of the trading success achieved by my advisor in real-life scenarios. You see, I am fortunate to collaborate with one of the prominent hedge funds, which graciously provides me with privileged access to insider information. It is on the foundation of this invaluable intelligence that I meticulously crafted my advisor.
In utmost reverence for the principles of legality and ethical conduct, I must emphasize the importance of maintaining strict compliance with applicable regulations and ensuring a level playing field for all market participants. The insights I receive from this collaboration serve as a valuable input in the development of my advisor's strategies, enhancing its ability to navigate the intricate dynamics of the financial landscape.
By synergizing the acquired insights with the prowess of my advisor, I endeavor to optimize my trading performance, effectively mitigating risks and capitalizing on emerging opportunities. It is through this refined approach that I strive to achieve sustainable success and uphold the principles that underpin the integrity of financial markets.
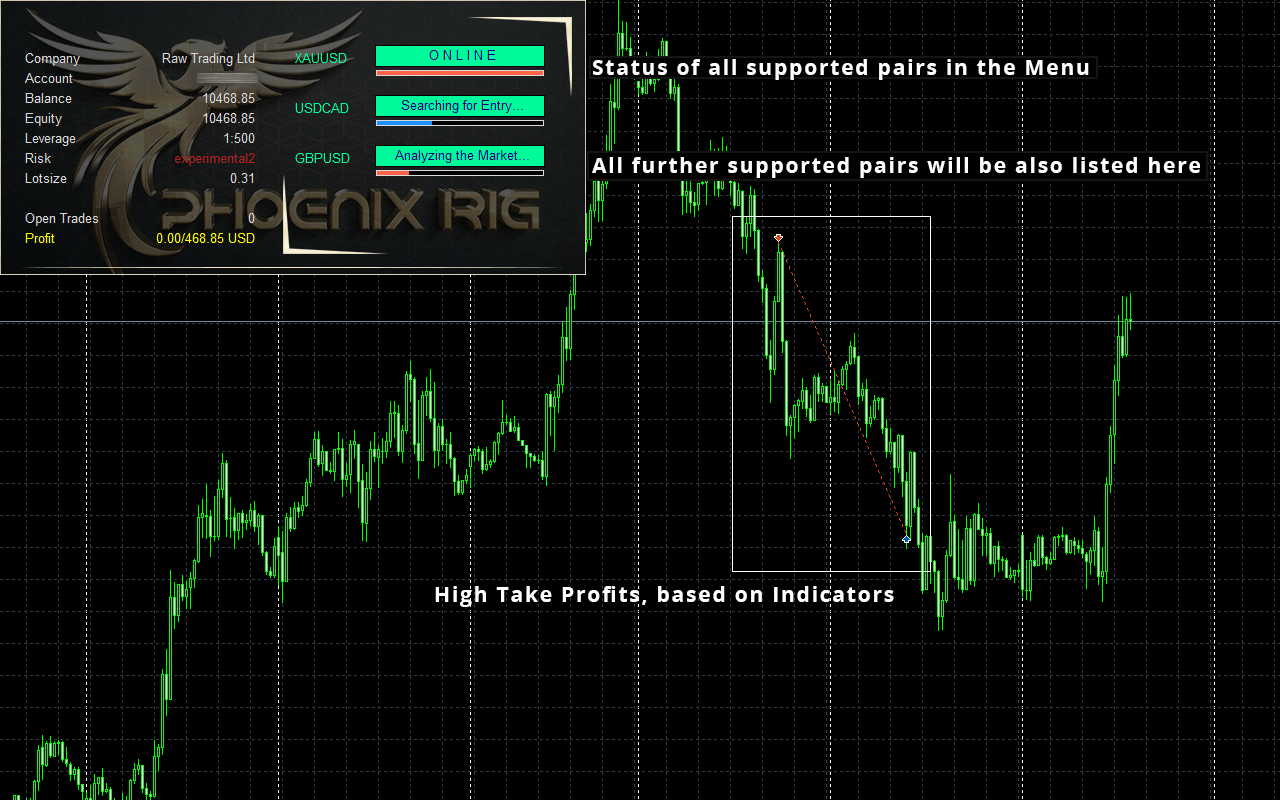
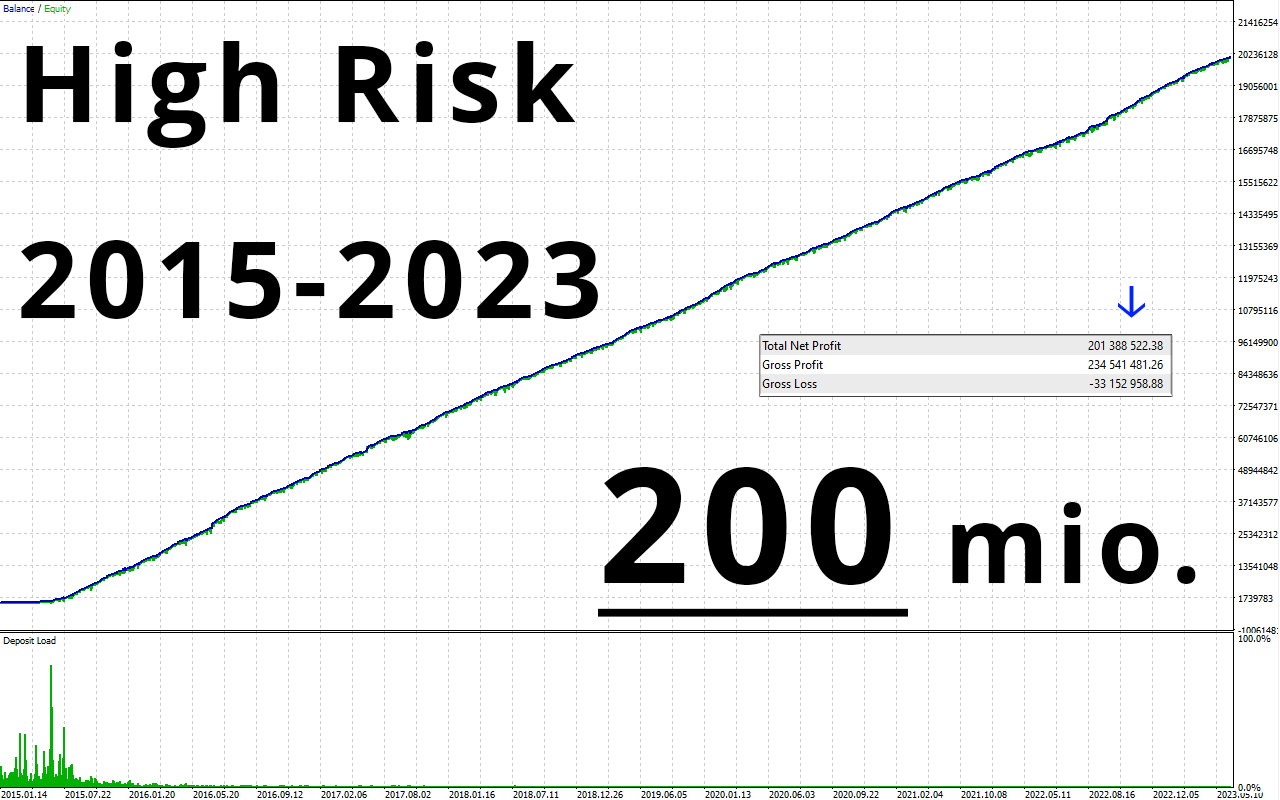
Real Signal: https://www.mql5.com/en/signals/1991005