Diskussion zum Artikel "Ökonometrischer Ansatz zur Chartanalyse"

Neuer Kommentar
 

Neuer Artikel Ökonometrischer Ansatz zur Chartanalyse :

Dieser Beitrag beschreibt die ökonometrischen Analysemethoden, die Autokorrelationsanalyse und insbesondere die Analyse von bedingten Varianzen. Worin liegt der Vorteil des hier beschriebenen Ansatzes? Die Arbeit mit nicht-linearen GARCH-Modellen erlaubt eine formelle Repräsentation der analysierten Serien vom mathematischen Gesichtspunkt aus, sowie die Erzeugung einer Prognose für eine festgelegte Anzahl an Schritten.

Autor: Dennis Kirichenko

 
Eine Verteilung, deren Insularität geringer ist als die einer Normalverteilung, hat eine «толстые хвосты»

Dies ist grundlegend falsch.

Erstens: Sprechen wir auf Russisch und nennen wir "Kurtosis" und "Insularität" mit dem üblichen Begriff - Kurtosis-Koeffizient oder einfach Kurtosis.

Zweitens haben "Inselbildung" und "Fettschwänze" im Allgemeinen nichts miteinander zu tun. Hier ein Gegenbeispiel - die Laplace-Verteilung (zweiseitige Exponentialverteilung), der die Graphen der allermeisten Finanzzeitreihen gehorchen. Ihr Exzess ist gleich 3 (d. h. ihre Spitze ist schärfer als die der Normalverteilung), aber die Schwänze sind dick - sie nehmen nach dem Gesetz exp(-x) ab, d. h. langsamer als bei der Gauß-Verteilung exp(-x^2).

[Gelöscht]  
alsu:

Das ist grundlegend falsch.

Erstens: Sprechen wir auf Russisch und nennen wir "Kurtosis" und "Insellage" mit dem anerkannten Begriff - Kurtosis-Koeffizient oder einfach Kurtosis.

Zweitens sind "Insellage" und "fette Schwänze" im Allgemeinen in keiner Weise miteinander verbunden. Hier ein Gegenbeispiel - die Laplace-Verteilung (zweiseitige Exponentialverteilung), der die Graphen der allermeisten Finanzzeitreihen gehorchen. Ihr Exzess ist gleich 3 (d. h. die Spitze ist schärfer als bei der Normalverteilung), aber die Schwänze sind einfach dick - sie nehmen nach dem Gesetz exp(-x) ab, d. h. langsamer als bei der Gauß-Verteilung exp(-x^2).

Außerdem gibt es kein Konzept des "Exzesses" an sich, sondern ein Konzept des "Exzessverhältnisses", das ein Maß für ein anderes Konzept "Exzess der Verteilung" ist, und dieses Konzept ist nur für unimodale Verteilungen definiert. Um diesen Koeffizienten richtig zu verwenden, muss also erstens die empirische Verteilungsfunktion bestimmt werden, was aus Sicht der Mathematik keine triviale Aufgabe ist, und zweitens muss im Rahmen einiger probabilistischer Kriterien die Hypothese geprüft und akzeptiert werden, dass die Verteilung einen einzigen Modus hat, was bei Finanzreihen nicht immer gegeben ist und ebenfalls eine nicht triviale Aufgabe darstellt. Ohne diese Schritte ist eine weitere Berechnung unmöglich, wenn sie den "Exzesskoeffizienten" erfordert.


P.S..


Es wird nichts darüber geschrieben, was zu tun ist, wenn der Test ergibt, dass die Reihe nicht für das angenommene Modell geeignet ist.

Es wird nichts darüber gesagt, warum und auf welcher Grundlage eine Reihe von so genannten "Erträgen" und nicht eine andere verwendet wird.

In der Praxis ist der Hauptgrund, warum die Arbeit mit Renditen von Vermögenswerten der Arbeit mit direkten Vermögenspreisen vorzuziehen ist, der, dass Renditen attraktivere statistische Eigenschaften haben.

Welche, wie attraktiv und zu welchem Zweck? Warum attraktiv und nicht zweckmäßig? Welches ist ein gültiges mathematisches Kriterium für die Wahl der Art der Transformation?
 
Liebe Kolleginnen und Kollegen, vielen Dank für Ihre Aufmerksamkeit für diesen Artikel. Wenn möglich, werde ich versuchen, alle Fragen und Kritikpunkte zu beantworten. Wenn Sie sich für das Thema interessieren, lesen Sie bitte die am Ende des Artikels aufgeführte Literatur. Viele Fragen werden sich dann von selbst erledigen.
 

alsu:

...Sprechen wir Russisch und nennen wir "Kurtosis" und "Islandness" mit dem anerkannten Begriff - Koeffizient des Exzesses oder einfach Exzess....

Besonders gefallen hat mir, dass alsu die Worte "Koeffizient" und "Exzess" als russisch betrachtet...

 

alsu:

Zweitens haben "Insellage" und "fette Schwänze" im Allgemeinen nichts miteinander zu tun. Hier ein Gegenbeispiel - die Laplace-Verteilung (zweiseitige Exponentialverteilung), der die Graphen der allermeisten Finanzzeitreihen gehorchen. Ihr Exzess ist gleich 3 (d. h. die Spitze ist schärfer als bei der Normalverteilung), aber die Schwänze sind einfach dick - sie nehmen nach dem Gesetz exp(-x) ab, d. h. langsamer als bei der Gauß-Verteilung exp(-x^2).

Das ist genau das, was meiner Meinung nach im Allgemeinen damit zusammenhängt.

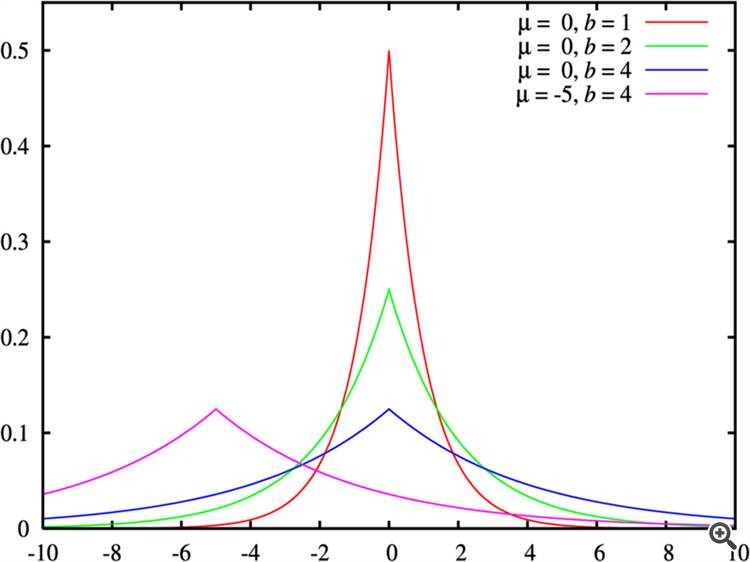
Ein Beispiel für "weniger Kurtosis - dickere Schwänze" ist in Abb. "Laplace-Verteilungen mit verschiedenen Parametern"dargestellt .


 

Ich würde meinem Artikel nur folgenden Satz hinzufügen: "Die Verteilung einer Reihe von Renditen weist häufiger ein Fat-Tail-Verhalten auf als die Normalverteilung." Das Phänomen der "fat tails" wird in der englischsprachigen Literatur als excess kurtosis bezeichnet. Diejenigen Reihen, deren Verteilungen solche Schwänze aufweisen, werden als leptokurtisch bezeichnet und haben eine positive Kurtosis (die die Kurtosis der Normalverteilung übersteigt).

Nun zum Kurtosis-Koeffizienten:

DieNormalverteilung hat eine Wölbung von Null, γ2 = 0.

Wenn die Schwänze der Verteilung "heller" sind und der Scheitelpunkt schärfer ist als bei der Normalverteilung, dann ist γ2 > 0.

Wenn die Schwänze der Verteilung "schwerer" sind und die Spitze "flacher" ist als bei der Normalverteilung, dann ist γ2 < 0.

 
denkir:

Ich würde eine solche Anregung nur in meinen Artikel aufnehmen:

Ergänzen Sie ihn. Wir werden ihn neu veröffentlichen.
[Gelöscht]  
denkir:

Ich würde meinem Artikel nur folgenden Satz hinzufügen: "Die Verteilung einer Reihe von Renditen weist häufiger ein Fat-Tail-Verhalten auf als die Normalverteilung." Das Phänomen der "fat tails" wird in der englischsprachigen Literatur als excess kurtosis bezeichnet. Diejenigen Reihen, deren Verteilungen solche Schwänze aufweisen, werden als leptokurtisch bezeichnet und haben eine positive Kurtosis (die die Kurtosis der Normalverteilung übersteigt).

Nun zum Kurtosis-Koeffizienten:

DieNormalverteilung hat eine Wölbung von Null, γ2 = 0.

Wenn die Schwänze der Verteilung "heller" sind und der Scheitelpunkt schärfer ist als bei der Normalverteilung, dann ist γ2 > 0.

Wenn die Schwänze der Verteilung "schwerer" sind und die Spitze "flacher" ist als bei der Normalverteilung, dann ist γ2 < 0.

Falsch, und wiki hat Fehler. Nehmen wir die Gleichverteilung. Ihr Überschuss kann berechnet werden, und sie hat überhaupt keine Schwänze. Man hat Ihnen also richtig gesagt, dass es im allgemeinen Fall keinen Zusammenhang zwischen der Schwere, der Länge, dem Vorhandensein von Schwänzen und dem Kurtosis-Koeffizienten gibt. Nehmen Sie eine Dreiecksverteilung - das ist das Gleiche.
 

Während Sie sich über Begriffe streiten, habe ich über Nacht bereits einige profitable EAs mit Ideen aus diesem Artikel gebaut. :-)

Allerdings sind ihre Gewinne sehr gering, obwohl sie recht stabil sind (überprüft an der Geschichte von 12 Jahren, die Charts wachsen schön). Die Korrelationen, die mit den im Artikel beschriebenen Methoden ermittelt werden, sind eher schwach (die Autokorrelationskoeffizienten der Reihen liegen bei etwa 0,01, in Ausnahmefällen bei 0,1, je nachdem, welche Preisderivate korreliert sind), und beim Handel wird der Gewinn aus ihnen stark vom Spread übertroffen. Ich musste einen Filter hinzufügen, um nur bei starken Signalen zu handeln, da sonst die Rentabilitätskurve quasi gerade nach unten gehen würde.

Auf jeden Fall vielen Dank an den Autor. Die Ideen sind wertvoll. Ich denke, dass Kritiker die Nase des Autors nicht in die Abgründe der Matheorie stecken sollten, sondern den Artikel als Hinweis auf ein weites Feld für praktische Experimente betrachten sollten.

[Gelöscht]  
ds2:

Während Sie sich über Begriffe streiten, habe ich über Nacht bereits einige profitable EAs mit Ideen aus diesem Artikel gebaut. :-)

Allerdings sind ihre Gewinne sehr gering, obwohl sie recht stabil sind (überprüft an der Geschichte von 12 Jahren, die Charts wachsen schön). Die Korrelationen, die mit den im Artikel beschriebenen Methoden ermittelt werden, sind eher schwach (die Autokorrelationskoeffizienten der Reihen liegen bei etwa 0,01, in Ausnahmefällen bei 0,1, je nachdem, welche Preisderivate korreliert sind), und beim Handel wird der Gewinn aus ihnen stark vom Spread übertroffen. Ich musste einen Filter hinzufügen, um nur bei starken Signalen zu handeln, da sonst die Rentabilitätskurve quasi gerade nach unten gehen würde.

Auf jeden Fall vielen Dank an den Autor. Die Ideen sind wertvoll. Ich denke, die Kritiker sollten die Nase des Autors nicht in die Abgründe der Matheorie stecken, sondern den Artikel als Hinweis auf ein weites Feld für praktische Experimente betrachten.

Und sind Sie der Meinung, dass die Kritiker bei der Verteidigung der These anwesend sein sollten, oder sollten sie die These ohne Verteidigung akzeptieren und mit der praktischen Forschung beginnen? Ich denke, es wird Sie interessieren, dass die Korrelationen nicht korrekt berechnet sind. Kritik ist dazu da, das Material zu verbessern, niemand behauptet, dass der Artikel gut ist. Damit der Gewinn für Ihre Systeme nicht gering ist, sondern größer wird.
123456789101112
Neuer Kommentar