Если я правильно понял, ты мы хотим найти максимум функции Hill равный 1.
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //global max + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //global min - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
У этой функции всего два параметра.
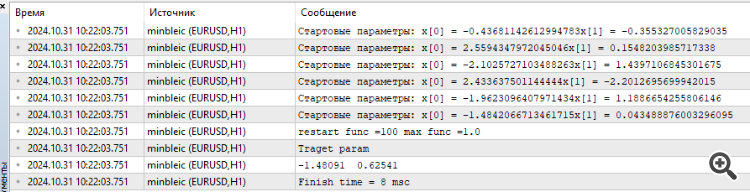
Подключил MinBleic
Мне кажется нужно считать не средний результат который выдает оптимизатор, а максимальный. Ну и время конечно вы видите, феноменальные 8 миллисекунд.
1. Если я правильно понял, ты мы хотим найти максимум функции Hill равный 1.
2. У этой функции всего два параметра.
3. Подключил MinBleic
Мне кажется нужно считать не средний результат который выдает оптимизатор, а максимальный. Ну и время конечно вы видите, феноменальные 8 миллисекунд.
Спасибо за комментарий.
1. Да, верно. Все тестовые функции унифицированы и их значения лежат в диапазоне [0.0; 1.0].
2. У всех тестовых функций только два параметра. Но при тестировании алгоритмов используем многомерное пространство поиска (три типа тестов, 5*2=10, 25*2=50, 500*2=1000 параметров, чтобы оценить способность AO к масштабированию) путём многократного дублирования двумерной функции.
3. Задача с двумя параметрами слишком простая для адекватного сравнения алгоритмов между собой, практически все алгоритмы решают такую задачу мгновенно со 100% сходимостью. Трудности возникают у алгоритмов как раз с многомерными пространствами.
Брать ли максимальный результат? Дело в том, что имеет значение разброс результатов в отдельных запусках алгоритмов. Во всех алгоритмах на первой итерации рандомные значения посева точек, которые могут оказаться совершенно случайно очень близки к значению глобального экстремума, в таком случае алгоритм неоправданно быстро найдет лучший результат, поэтому среднее значение от результатов запусков лучше отражает характеристику работы алгоритма, чтобы исключить рандомную зависимость от "успеха" алгоритма.
Это связано с теорией вероятностей. Какой бы сложной не была целевая функция, но если параметр всего один, то даже сгенерировав 10 случайных значений одно из них окажется очень близко к глобальному экстремуму. Методы ALGLIB (вариации градиентного спуска) чувствительны к начальному положению точек в пространстве и так же относятся к детерминированной природе этих методов. С увеличением мерности пространства поиска сложность пространства увеличивается экспоненциально, уже никак не получится попасть в глобальный экстремум путем генерации случайных чисел.
Доказательством служат трудности этих методов сойтись даже на монотонном, гладком, унимодальном параболоиде, если мерность задачи возрастает.
Чем более стабильные результаты показывает AO независимо от начальных значений в пространстве поиска, тем больше этот метод может считаться надёжным в решении задач. Именно поэтому в тестировании выбираем среднее значение из множественных запусков AO.
Сегодняшние реалии таковы, что во многих задачах требуется оптимизировать миллионы, и даже миллиарды параметров (ИИ, LLM, генеративные сети, сложные комплексные задачи управления на производстве и бизнесе), при этом о гладкости и унимодальности задач говорить не приходится.
Спасибо за комментарий.
1. Да, верно. Все тестовые функции унифицированы и их значения лежат в диапазоне [0.0; 1.0].
2. У всех тестовых функций только два параметра. Но при тестировании алгоритмов используем многомерное пространство поиска (три типа тестов, 5*2=10, 25*2=50, 500*2=1000 параметров, чтобы оценить способность AO к масштабированию) путём многократного дублирования двумерной функции.
3. Задача с двумя параметрами слишком простая для адекватного сравнения алгоритмов между собой, практически все алгоритмы решают такую задачу мгновенно со 100% сходимостью. Трудности возникают у алгоритмов как раз с многомерными пространствами.
Брать ли максимальный результат? Дело в том, что имеет значение разброс результатов в отдельных запусках алгоритмов. Во всех алгоритмах на первой итерации рандомные значения посева точек, которые могут оказаться совершенно случайно очень близки к значению глобального экстремума, в таком случае алгоритм неоправданно быстро найдет лучший результат, поэтому среднее значение от результатов запусков лучше отражает характеристику работы алгоритма, чтобы исключить рандомную зависимость от "успеха" алгоритма.
Это связано с теорией вероятностей. Какой бы сложной не была целевая функция, но если параметр всего один, то даже сгенерировав 10 случайных значений одно из них окажется очень близко к глобальному экстремуму. Методы ALGLIB (вариации градиентного спуска) чувствительны к начальному положению точек в пространстве и так же относятся к детерминированной природе этих методов. С увеличением мерности пространства поиска сложность пространства увеличивается экспоненциально, уже никак не получится попасть в глобальный экстремум путем генерации случайных чисел.
Доказательством служат трудности этих методов сойтись даже на монотонном, гладком, унимодальном параболоиде, если мерность задачи возрастает.
Чем более стабильные результаты показывает AO независимо от начальных значений в пространстве поиска, тем больше этот метод может считаться надёжным в решении задач. Именно поэтому в тестировании выбираем среднее значение из множественных запусков AO.
Сегодняшние реалии таковы, что во многих задачах требуется оптимизировать миллионы, и даже миллиарды параметров (ИИ, LLM, генеративные сети, сложные комплексные задачи управления на производстве и бизнесе), при этом о гладкости и унимодальности задач говорить не приходится.
Вы взяли очень сложную функцию саму по себе. С ростом числа параметров нахождение оптимальных параметров для суммы таких функций несет в себе чисто теоретический интерес на мой взгляд. Для трейдинга прогнозная математическая модель может иметь много параметров, но сама функция потерь очень простая, поэтому там поиск происходит гораздо легче. И уж тем более там не может быть миллиард параметров, а какие-то скромные 10-100, если нас интересует не курвафиттинг конечно, имхо.
Если посмотреть с точки зрения результата. Вот меня интересуют параметры, которые находят максимум функции, зачем мне средний результат ? Меня интересует оптимум и время достижения этого оптимума. Если это время приемлемо, тогда мне все равно сколько компьютер потратил усилий для выбора стартового вектора параметров, главное что я получил результат.
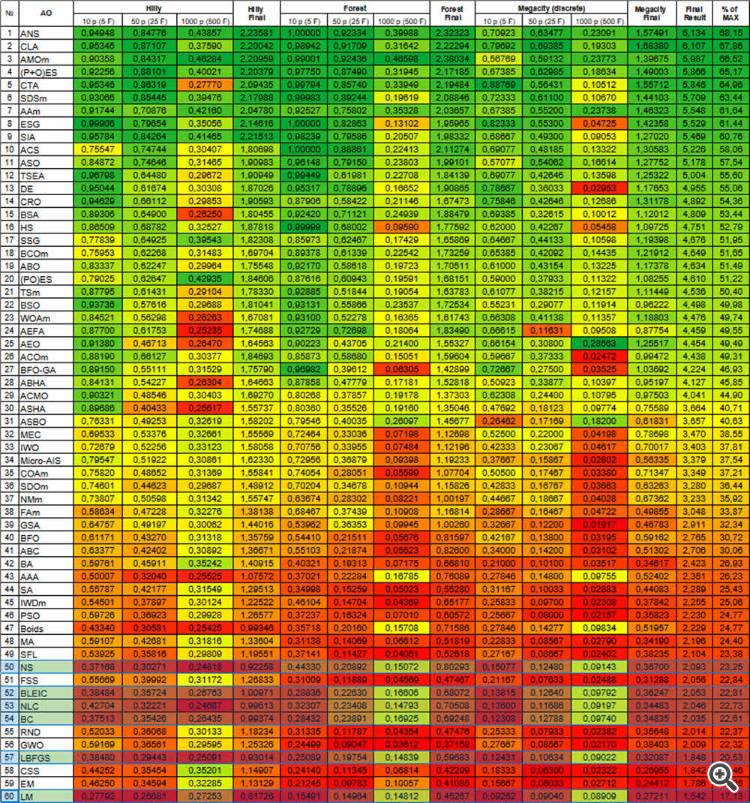
Вот пример для суммы 5 функций Hilly
15 секунд времени и результат 0,76. Неплохо я считаю. Особенно учитывая трейдерскую тематику, когда мы просто не знаем чему равен глобальный оптимум и никогда не будем этого знать.
В любом случае спасибо за статью. Здесь есть о чем подумать. Я чуть позже протестирую остальные алгоритмы и выложу результат.
1) Вы взяли очень сложную функцию саму по себе. С ростом числа параметров нахождение оптимальных параметров для суммы таких функций несет в себе чисто теоретический интерес на мой взгляд.
2) Для трейдинга прогнозная математическая модель может иметь много параметров, но сама функция потерь очень простая, поэтому там поиск происходит гораздо легче. И уж тем более там не может быть миллиард параметров, а какие-то скромные 10-100, если нас интересует не курвафиттинг конечно, имхо.
3) Если посмотреть с точки зрения результата. Вот меня интересуют параметры, которые находят максимум функции, зачем мне средний результат ? Меня интересует оптимум и время достижения этого оптимума. Если это время приемлемо, тогда мне все равно сколько компьютер потратил усилий для выбора стартового вектора параметров, главное что я получил результат.
4) Вот пример для суммы 5 функций Hilly
15 секунд времени и результат 0,76. Неплохо я считаю. Особенно учитывая трейдерскую тематику, когда мы просто не знаем чему равен глобальный оптимум и никогда не будем этого знать.
5) В любом случае спасибо за статью. Здесь есть о чем подумать. Я чуть позже протестирую остальные алгоритмы и выложу результат.
1) В статьях рассматриваем AO не сами по себе, как некий конь в вакууме (пример - PSO, очень известный и поэтому популярный, но не мощный, а тот же AEO - вообще никому не известен, но рубит гладкое и дискретное пространство аж щепки летят), а наряду с разбором их логики и устройства рассматриваем их поисковые способности по сравнению друг с другом. Это позволяет глубоко понять их потенциальные возможности именно в практических задачах. И именно с ростом размерности можно раскрыть истинные возможности и именно в сравнении алгоритмов между собой. В реальной жизни практически не бывает простых задач, если конечно речь не идет о задачах, которые можно решить аналитически.
Выше пояснил, почему при сравнении алгоритмов необходимо использовать среднее значение итоговых результатов - чтобы исключить влияние "случайного успеха" и выявлять непосредственно поисковые возможности алгоритмов.
А когда дело касается практического применения AO (а не для сравнения AO-ов), то да, рекомендуется использовать несколько запусков оптимизаций, чтобы выбрать потом наилучший результат. Но, если один слабый алгоритм приходится многократно перезапустить, тратя на этой драгоценные запуски целевой функции, то другой достигнет того же результата за гораздо меньшее количество запусков целевой функции. Зачем платить больше, если результат может быть таким же? Слабые алгоритмы будут застревать, вязнуть в пространстве поиска, требуя многократных перезапусков и вы никогда не будете уверены, что элементарно не застряли в самом начале оптимизации. Полагаю, такая ситуация никому не интересна на практике.
2) Попробуйте визуализировать функцию потерь на практической задаче хотя бы с двумя параметрами с каким нибудь советником, поверхность окажется вовсе не гладкой и не унимодальной. В виду дискретной природы трейдерских задач - простых и гладких целевых просто не существует. Поэтому методы, испытывающие трудности даже на гладком параболоиде, будут неэффективны в трейдинге.
3) Средний результат используется для сравнения алго между собой, а не на практике (см. п.1). Если не важно время и энергия, потраченное на поиск, то сделайте полный перебор, нет смысла использовать AO вообще. Но практике такое бывает крайне редко, мы всегда ограничены во времени и вычислительных ресурсах.
4) В представленных результатах отсутствует информация о количестве запусков целевой функции, необходимом для достижения указанного результата. Этот показатель является ключевым при оценке эффективности AO. Выбор AO должен основываться на максимальной эффективности (минимизации количества запусков) и минимизации вероятности застревания, особенно в практических задачах трейдинга.
5) Спасибо, рад, что статьи дают почву для рассуждений. Будет очень здорово, если приведёте код проведённых испытаний, хотя, весь код уже предоставлен в статье (судя по всему, используете какой-то свой способ тестирования). Будем смотреть, разбираться.
Работаю над отдельной статьёй по затронутым вопросам в этом обсуждении.
Пробуйте разные алгоритмы, мы рассмотрели многие, сравнивайте их между собой. Алглибовские методы очень быстрые и полагаю, что они очень хороши для решения аналитически сформулированных задач (это отдельная тема), но там, где аналитическая формула не известна, то есть другие варианты.
Для тех, кому необходимо решать аналитические задачи - статьи также будут очень полезны, так как в них описаны сами принципы работы с методами ALGLIB.
Не корректно сравнивать метаэвр. и градиентные солверы таким образом. Их нужно поставить в равные условия.
Метаэвр. уже имеют посев точек, а градиентные начинают из одной точки.
Чтобы создать равные условия, нужно сделать батчинг для вторых. Либо множественную инициализацию.
Поэтому градиентные нужно оценивать по лучшему, а не среднему результату. И поэтому они быстрее работают. Это дает баланс скорости и точности в обучении нейросетей.
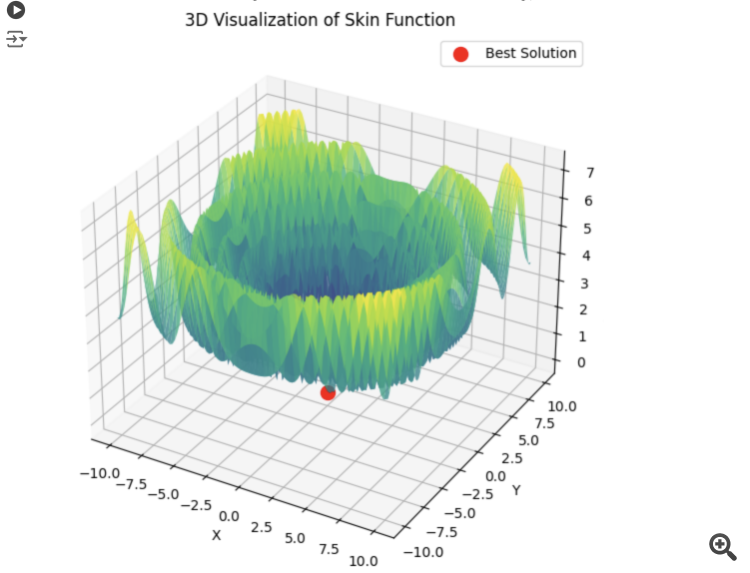
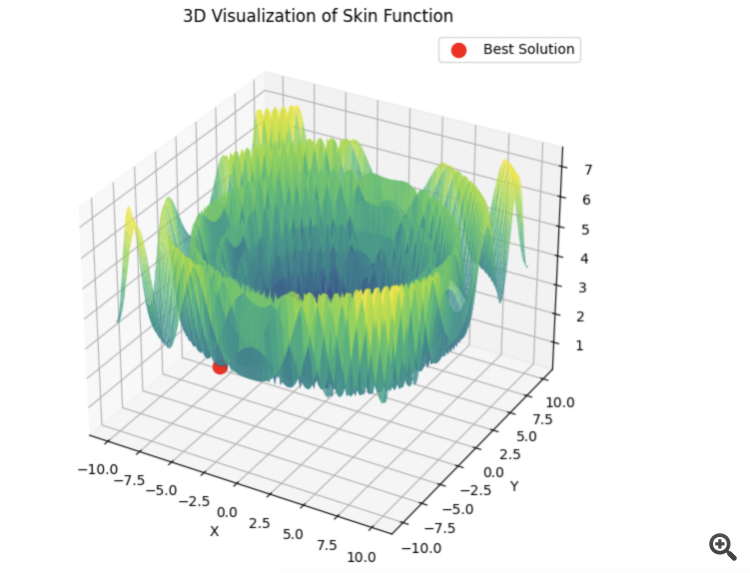
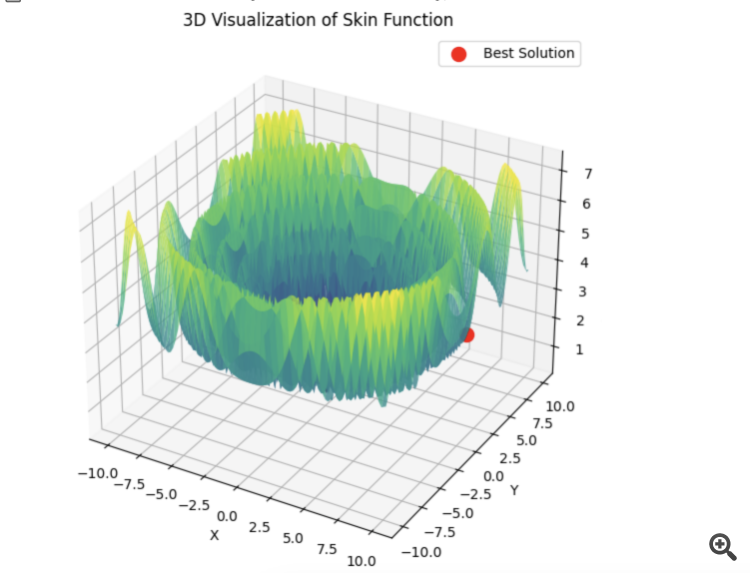
Если PSO сразу выбирает правильный минимум:
То lbfgs будет скакать от локала к локалу, и это нормальное для него поведение. Зато быстро и можно скакать настраивоемое кол-во раз, разделяя оптимизируемую ф-ю на батчи.
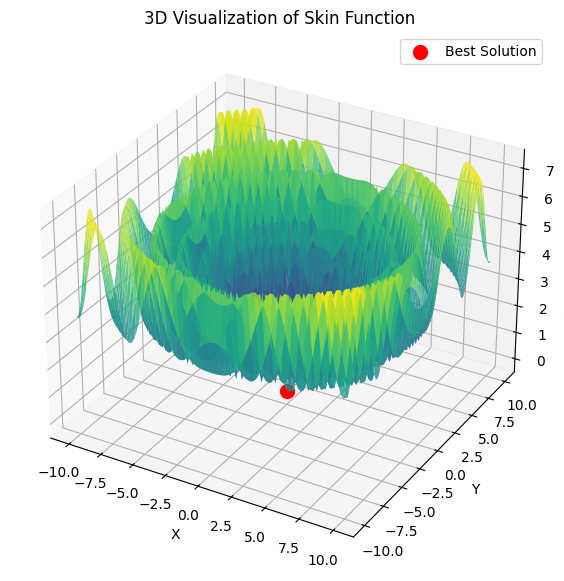
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

Опубликована статья Методы оптимизации библиотеки Alglib (Часть II):
В статье продолжим изучение оставшихся методов оптимизации из библиотеки ALGLIB, уделяя особое внимание их тестированию на сложных многомерных функциях. Это позволит нам не только оценить эффективность каждого из алгоритмов, но и выявить их сильные и слабые стороны в различных условиях.
В первой части нашего исследования, посвященного алгоритмам оптимизации библиотеки ALGLIB в стандартной поставке терминала MetaTrader 5, мы детально познакомились с алгоритмами: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) и NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). Мы не только рассмотрели их теоретические основы, но и разобрали простой способ применения для задач оптимизации.
В настоящей статье мы продолжим исследование оставшихся методов из арсенала ALGLIB. Особое внимание будет уделено их тестированию на комплексных многомерных функциях, что позволит нам сформировать целостное представление об эффективности каждого метода. В завершение проведем всесторонний анализ полученных результатов и представим практические рекомендации по выбору оптимального алгоритма для конкретных типов задач.
Автор: Andrey Dik