СОПРОВОЖДЕНИЕ ЭКСПЕРИМЕНТА ПО АНАЛИЗУ ДАННЫХ ФОРЕКСА: разведка и пилотное обучение
Начало по ссылкам:
https://www.mql5.com/ru/blogs/post/659572
https://www.mql5.com/ru/blogs/post/659929
https://www.mql5.com/ru/blogs/post/660386
Сегодня
Кода будет поменьше, но поясню его подробнее. Еще раз проведу разведывательный анализ, что не успел в прошлый раз. Далее создадим архитектуру для обучения машины, обучим ее в режиме "лайт" и сделаем анализ результатов.
Посчитаем и визуализируем линейные корреляции между всеми признаками и целевыми переменными:
### Correlation matrix heatmap { cormat <- round(cor(dat_train_final), 3) # Get lower triangle of the correlation matrix get_lower_tri<-function(cormat){ cormat[upper.tri(cormat)] <- NA return(cormat) } # Get upper triangle of the correlation matrix get_upper_tri <- function(cormat){ cormat[lower.tri(cormat)]<- NA return(cormat) } upper_tri <- get_upper_tri(cormat) library(reshape2) melted_cormat <- melt(upper_tri, na.rm = TRUE) library(ggplot2) ggplot(data = melted_cormat, aes(Var2, Var1, fill = value))+ geom_tile(color = "white")+ scale_fill_gradient2(low = "blue", high = "red", mid = "white", midpoint = 0, limit = c(-1,1), space = "Lab", name = "Pearson\nCorrelation") + theme_minimal()+ theme(axis.text.x = element_text(angle = 90, vjust = 1, size = 10, hjust = 1))+ coord_fixed() }
Вот так наглядно получилось. Видно, что входные переменные связаны (они идут слева), а целевые переменные слегка отрицательно коррелируют с входами (правые столбики).
Теперь посчитаем и нарисуем автокорреляцию для всех переменных. Я хочу видеть, что у меня вектора для обучения разделены по времени достаточно, что не быть сильно зависимыми:
### Autocorrelations { acflist <- list() for (i in 1:126){ acflist[[i]] <- acf(x = dat_train_final[, i], lag.max = 10 , type = "correlation" , plot = TRUE , na.action = na.fail) } i <- 125 print(plot(acflist[[i]] , main = paste(names(dat_train_final)[i], ": autocorrelogram"))) }
Выведем для переменной № 125 автокоррелограмму:
Это целевая переменная - заглядывание в будущее на 512 минут. Видно, что на 2 и 4 лагах отрицательно коррелирует с собой. Это связано с тем, что разделение векторов данных идет 724 +- 50 минут и лаг 2 это значения примерно сутки назад, и в самих данных форекс есть такая корреляция. В общем, ничего страшного.
Моделирование
Мы моделируем зависимости в данных, не что-то иное. Если проверка модели на валидационной выборке показывает плохое качество, значит либо машина не выучила зависимости, либо данные нестационарны и зависимости изменились, либо то и другое вместе.
В первую очередь я буду обучать Gradient Boosting Machine (GBM): https://en.wikipedia.org/wiki/Gradient_boosting
Это разновидность random forest, считается очень сильным аппроксиматором. Примерно идею его работы можно сформулировать так: каждое последующее дерево решений строится так, чтобы улучшить аппроксимацию подпространства целевой переменной, которая дала наибольшую ошибку на предыдущем дереве.
Нужно загрузить библиотеки
############## ################## ###################### ######################### MOdelling with GBM ###################### ################## ############## ### loading working data dat_train_final <- read.csv('C:/R_study/fx/dat_train_final.csv' , sep = ',' , dec = '.') dat_test_final <- read.csv('C:/R_study/fx/dat_test_final.csv' , sep = ',' , dec = '.') library(caret) library(gbm) library(doParallel)
Затем мы решаем какую функцию ошибки модель будем минимизировать. Для нашего типа данные доступно: квадратные ошибки и абсолютные ошибки. В первую очередь я пробую минимизировать квадратные ошибки. Для этого я пишу свою функцию maemetrics, которая будет подставляться в функцию библиотеки caret. В этой функции я считаю среднюю абсолютную ошибку, аналог R ^ 2 для абсолютных ошибок (насколько предсказания лучше уменьшают ошибку, чем среднее значение по целевой переменной). Далее среднеквадратичную ошибку и обычный R ^ 2 (насколько предсказания улучшают квадрат ошибок по сравнению со средней).
############################ Gaussian distribution
maemetrics <- function (data,
lev = NULL,
model = NULL) {
mae <- mean(abs(data$obs - data$pred))
mae_improve <- 1 - sum(abs(data$obs - data$pred)) / sum(abs(data$obs - mean(data$obs)))
mse <- mean((data$obs - data$pred) ^ 2)
rsq <- 1 - sum((data$obs - data$pred) ^ 2) / sum((data$obs - mean(data$obs)) ^ 2)
out <- c(mae, mae_improve)
names(out) <- c('mae', 'mae_improve', 'mse', 'rsq')
out
}
Далее зададим перебор параметров модели и методику работы с данными и результатами. Как видно, caret дает возможность оптимизировать 4 параметра GBM:
глубину дерева (а точнее, количества уникальных переменных в одной ветви)
количество деревьев
скорость обучения
минимальное количество примеров в терминальном ноде
Обработка данных будет идти, как я уже говорил, кроссвалидацией с разделением обучающего набора на 5 частей. Перебор параметров будет сплошной по указанной сетке. Даем возможность параллелить вычисления.
# tuning GBM gbmGrid <- expand.grid(interaction.depth = seq(from = 6, to = 11, by = 5) , n.trees = seq(from = 300, to = 700, by = 200) , shrinkage = seq(from = 0.01, to = 0.05, by = 0.04) , n.minobsinnode = seq(from = 70, to = 150, by = 40)) # prepare training scheme gbmControl <- trainControl(method = 'cv' , number = 5 , verboseIter = F , returnData = F , returnResamp = 'all' , savePredictions = 'none' , summaryFunction = maemetrics , search = 'grid' , allowParallel = T)
Далее выберем одну из целевых переменных - это заглядывание в будущее на 2 минуты и все предикторы. Запустим копии программы для 4 ядер и приступим к обучению.
Обратите внимание, что я указываю distribution = 'gaussian'
это параметр из GBM, который говорит о том, что минимизируются квадраты ошибок, metric = 'rsq'
это указание на ту метрику, по которой обучалка предложит нам лучшую модель, и maximize = T
метрика должна быть максимальной.
# train the model inputs <- names(dat_train_final)[1:108] output <- 'future_lag_2' lag2_train_set <- dat_train_final[, c(eval(inputs), eval(output))] lag2_test_set <- dat_test_final[, c(eval(inputs), eval(output))] cores <- 4 #detectCores() cl <- makePSOCKcluster(cores) registerDoParallel(cl) gbm_lag2_models <- train(future_lag_2 ~ . , data = lag2_train_set , method = 'gbm' , distribution = 'gaussian' #, bag.fraction = 0.9 , trControl = gbmControl , metric = 'rsq' , maximize = T , tuneGrid = gbmGrid) stopCluster(cl)
После окончания обучения
# summarize the model print(gbm_lag2_models) summary(gbm_lag2_models) print(varImp(gbm_lag2_models, scale = FALSE)) print(gbm_lag2_models$bestTune) gbmModel_lag2_importance <- as.data.frame(varImp(gbm_lag2_models, scale = FALSE)[[1]]) gbmModel_lag2_importance$vars <- rownames(gbmModel_lag2_importance) lag2_gbm_models_arr <- as.data.frame(cbind(gbm_lag2_models[[4]][1] , gbm_lag2_models[[4]][2] , gbm_lag2_models[[4]][3] , gbm_lag2_models[[4]][4] , gbm_lag2_models[[4]][7] , gbm_lag2_models[[4]][8])) lag2_gbm_models_arr_ordered <- lag2_gbm_models_arr[order(lag2_gbm_models_arr$Rsquared, decreasing = T), ]
Выведем все обученные модели с их параметрами на отрезках кроссвалидации. Усредненную метрику по 5 фолдам и стандартное отклонение метрики.
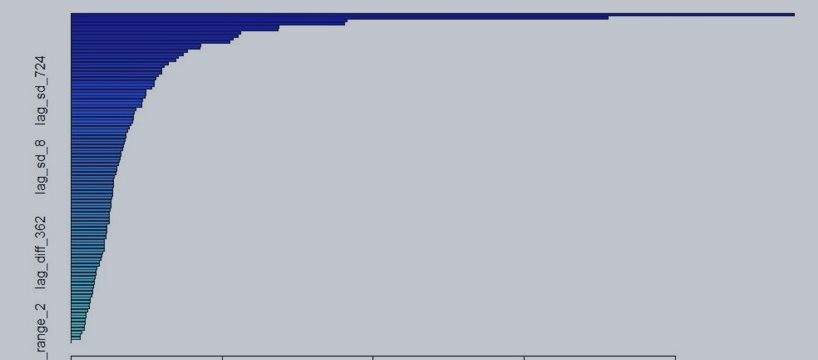
Важность предикторов:
> print(varImp(gbm_lag2_models, scale = FALSE)) gbm variable importance only 20 most important variables shown (out of 108) Overall lag_mean_diff_3 2511.2 lag_mean_diff_2 1864.9 lag_sd_181 958.0 lag_max_diff_2 949.6 lag_min_diff_3 720.2 lag_sd_2 719.2 lag_min_diff_4 588.7 lag_sd_64 580.2 lag_mean_diff_4 564.4 lag_sd_91 551.1 lag_mean_diff_6 451.3 lag_min_diff_2 446.2 lag_sd_256 405.1 lag_sd_128 389.8 lag_sd_45 373.2 lag_sd_362 362.9 lag_diff_11 339.1 lag_mean_diff_91 322.4 lag_diff_128 315.1 lag_range_181 315.0
Затем я вывожу таблицу результатов массив и сортирую его по целевой метрике.
Затем мы валидируем наши модели.
Обратите внимание, что я беру n лучших параметров моделей по их метрике на кроссвалидации, обучаю соответствующую модель уже на всем обучающем множестве и делаю проверку на валидационной выборке.
Для каждой из моделей я записываю в массив следующие параметры:
'method' - gbm
, 'target' - future_lag_2
, 'r_squared_train' - R^2 на кроссвалидации
, 'rmse_train' - корень квадрата ошибок на кроссвалидации
, 'r_squared_validate' - R^2 для валидационной выборки
, 'rmse_validate' - корень квадрата ошибок для валидационной выборки
, 'mae_validate' - средняя абсолютная ошибка (легко трактуется - средняя ошибка в пунктах)
, 'mae_mean_improve' - аналог R^2 для абслютных ошибок
, 'mae_zero_improve' - улучшение ошибок предсказаниями в смысле абсолютных ошибок по сравнению с нулем (не со средним)
, 'r_squared_zero_improve' - улучшение предсказания квадратных ошибок по сравнению с нулем.
# train best models lag2_validating_arr <- data.frame() max_best_models <- 5 lag2_validating_arr[1:max_best_models, 1] <- 'GBM' lag2_validating_arr[1:max_best_models, 2] <- output for (i in 1:max_best_models){ lag2_gbm_obj <- gbm(future_lag_2 ~ . , data = lag2_train_set , distribution = "gaussian" , n.trees = lag2_gbm_models_arr_ordered$n.trees[i] , interaction.depth = lag2_gbm_models_arr_ordered$interaction.depth[i] , n.minobsinnode = lag2_gbm_models_arr_ordered$n.minobsinnode[i] #, bag.fraction = 0.9 , shrinkage = lag2_gbm_models_arr_ordered$shrinkage[i] , verbose = T , n.cores = 3) # predict with best model lag2_gbm_predict <- predict(lag2_gbm_obj , newdata = lag2_test_set , n.trees = lag2_gbm_models_arr_ordered$n.trees[i] , type = "response") lag2_validate_predictions <- as.data.frame(lag2_test_set$future_lag_2) lag2_validate_predictions$predicted_values <- lag2_gbm_predict lag2_validate_predictions$residuals <- lag2_validate_predictions[, 1] - lag2_validate_predictions[, 2] lag2_validate_predictions$residuals_mean <- lag2_validate_predictions[, 1] - mean(lag2_validate_predictions[, 1]) lag2_validate_predictions$abs_res <- abs(lag2_validate_predictions$residuals) lag2_validate_predictions$abs_mean_res <- abs(lag2_validate_predictions$residuals_mean) lag2_validate_predictions$abs_zero_res <- abs(lag2_validate_predictions[, 1]) lag2_gbm_validate_r_sqr <- 1 - sum(lag2_validate_predictions$residuals ^ 2) / sum(lag2_validate_predictions$residuals_mean ^ 2) lag2_gbm_validate_rmser <- mean(lag2_validate_predictions$residuals ^ 2) ^ 0.5 lag2_gbm_validate_mae <- mean(lag2_validate_predictions$abs_res) lag2_gbm_validate_mae_mean <- 1 - sum(lag2_validate_predictions$abs_res) / sum(lag2_validate_predictions$abs_mean_res) lag2_gbm_validate_mae_zero <- 1 - sum(lag2_validate_predictions$abs_res) / sum(lag2_validate_predictions$abs_zero_res) lag2_gbm_validate_r_sqr_zero <- 1 - sum(lag2_validate_predictions$residuals ^ 2) / sum(lag2_validate_predictions[, 1] ^ 2) lag2_validating_arr[i, 3] <- lag2_gbm_models_arr_ordered$Rsquared[i] lag2_validating_arr[i, 4] <- lag2_gbm_models_arr_ordered$RMSE[i] lag2_validating_arr[i, 5] <- lag2_gbm_validate_r_sqr lag2_validating_arr[i, 6] <- lag2_gbm_validate_rmser lag2_validating_arr[i, 7] <- lag2_gbm_validate_mae lag2_validating_arr[i, 8] <- lag2_gbm_validate_mae_mean lag2_validating_arr[i, 9] <- lag2_gbm_validate_mae_zero lag2_validating_arr[i, 10] <- lag2_gbm_validate_r_sqr_zero } colnames(lag2_validating_arr) <- c( 'method' , 'target' , 'r_squared_train' , 'rmse_train' , 'r_squared_validate' , 'rmse_validate' , 'mae_validate' , 'mae_mean_improve' , 'mae_zero_improve' , 'r_squared_zero_improve' )
Что же получилось для этого конкретного эксперимента:
|
Дело в том, что на валидции все наши 5 лучших моделей сработали хуже, чем среднее значение и нуль. То есть, результат эксперимента не привел к "открытию".
Учитывая, что на кроссвалидации R^2 был в районе 2%, что говорит, о том, что на разных валютных парах за тот же период времени модель работает лучше, чем среднее, мы можем почти наверное сказать, что на валидацинном отрезке данные как-то поменялись (и зависимости также поменялись), что привело к тому, что модель даже хуже нулевого прогноза.
А теперь результаты эксперимента, где минимизировалась абсолютная ошибка:
|
Констатирую, что все метрики (и квадратные и абсолютные) для валидационной выборки также деградировали и стали хуже нулевого и среднего прогноза.
Кстати, для работы модели по минимизации абсолютной ошибки нужно немного поменять код:
gbm_lag2_models <- train(future_lag_2 ~ . , data = lag2_train_set , method = 'gbm' , distribution = 'laplace' #, bag.fraction = 0.9 , metric = 'mae_improve' , maximize = T , trControl = gbmControl , tuneGrid = gbmGrid)
Задано распределение Лапласса для GBM и максимизируется метрика на основе абсолютной ошибки.
Дальнейшие планы
Несмотря на отрицательный результат пилотного обучения я следующую (а может, и последующую) неделю буду обучать GBM с более широким разбросом параметров, и нужно будет протестировать не одну, а все 18 целевых переменных. Для каждой модели буду отбирать 10 лучших наборов параметров. Думаю, что где-то может и выстрелить.
Через 1-2 недели я собираюсь в таком же ключе обучать классический random forest, попробую ada boost, и прогремевший своей скоростью и точностью xGBoost. Возможно, одна из этих моделей покажет даже лучшие результаты. Нейросеть я не смогу хорошо обучить, так как давно уже с ними не работал, поэтому скорее всего не буду трогать.
GBM обучается долго, это даже мешает, и памяти есть много. Но как вы уже поняли работа предстоит затяжная и придется попробовать много вариантов.


