As seguintes referências estão disponíveis sobre o tema "Fundamentos da Análise de Regressão".
Davidson,Russell e James G. MacKinnon (1993). Estimativa e Inferência emEconometria, Oxford: Oxford University Press.
Greene, William H. (2008). Análise Econométrica, 6ª Edição, Upper Saddle River, NJ: Prentice-Hall.
Johnston, Jack e John Enrico DiNardo (1997). Econometric Methods, 4th Edition, New York: McGraw-Hill.
Pindyck, Robert S. e Daniel L. Rubinfeld (1998). Econometric Models and Economic Forecasts, 4th edition, New York: McGraw-Hill.
Wooldridge, Jeffrey M. (2000). Econometria introdutória: Uma abordagem moderna. Cincinnati, OH: South-Western College Publishing.
Deixe-me dar um exemplo de uma regressão, que nada mais é do que uma função (variável dependente) que depende de seus argumentos (variáveis independentes, regressores). Há vários passos a seguir ao calcular uma regressão:
1. Uma equação precisa ser anotada.
Eu tomo o MA calorosamente favorecido, mas ponderado, tão indulgente para mim, calculando-o usando as 5 barras anteriores (valores de defasagem). Eu escrevo a fórmula no formulário:
EURUSD = C(1)*EURUSD(-1) + C(2)*EURUSD(-2) + C(3)*EURUSD(-3) + C(4)*EURUSD(-4) + C(5)*EURUSD(-5)
2. estimativa
É necessário estimar o coeficiente c(i) desta equação para que a curva de nossa MA corresponda à série inicial de EURUSD_H1 anos tão boa quanto possível. Obtemos o resultado da avaliação dos coeficientes desconhecidos.
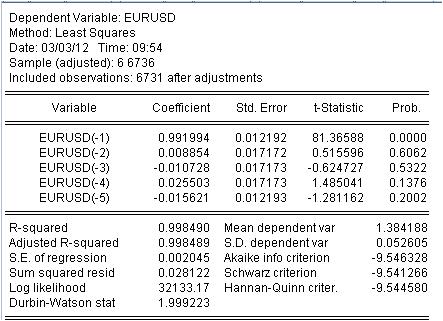
Obtivemos os valores de nossa MA ponderada. Nós temos a equação:
EURUSD = 0,991993934254*EURUSD(-1) + 0,00885362355538*EURUSD(-2) - 0,0107282369642*EURUSD(-3) + 0,0255027160774*EURUSD(-4) - 0,0156205779585*EURUSD(-5)
3. Resultados.
Que resultados vemos?
3.1 Primeiro de tudo, a própria equação Mach. Quero prestar atenção a uma pequena nuance. Quando calculamos uma simples máscara calculando a média, não a registramos no meio do intervalo, mas em seu final, por algum motivo. A regressão é usada para calcular o último valor com base nos anteriores.
3.2 Acontece que as proporções não são constantes, mas variáveis aleatórias com seu próprio desvio.
3.3 A última coluna diz que existe uma probabilidade não nula de que os coeficientes dados sejam zero.
4. Trabalhando com a equação
Vamos dar uma olhada em nossa mistura ponderada.

O mashka cobriu o cotier com tanta força que não pode ser visto, mas ainda há discrepâncias entre o cotier e o mashka. Aqui estão as estatísticas destas discrepâncias

Vemos uma grande dispersão de -137 pontos a 215 pontos. Embora o desvio padrão = 20 pontos.
Conclusão.
Recebemos uma qualidade invulgarmente alta da máscara com as características estatísticas conhecidas usando regressão.
O último. Yusuf! Não fique debaixo do bonde, não faça o público rir em mais um fio.
Pronto para discutir a literatura e a aplicação do tema da regressão.
3. Resultados.
Que resultados vemos?
3.1 Antes de mais nada, a própria equação Mach. Quero ressaltar aqui uma sutileza. Quando calculamos uma máscara simples obtendo a média, por alguma razão não colocamos esta média no meio do intervalo, mas em seu final. A regressão é usada para calcular o último valor com base nos anteriores.
3.2 Acontece que as proporções não são constantes, mas variáveis aleatórias!
3.3 A última coluna diz que há uma probabilidade não nula de que os coeficientes dados sejam zero.
1. Desculpe pelo sal extra na ferida - a série original é não-estacionária de qualquer forma.
2) Esta probabilidade é quase sempre diferente de zero.
3. Você já verificou a multicolinearidade? IMHO, se você eliminar a multicolinearidade, só resta uma variável. Você já determinou os fatores significativos?
4. Quantas observações você tem para 5 variáveis?
Como você é tão alfabetizado?
1. Desculpe pelo sal extra na ferida - a série original é não-estacionária de qualquer forma.
Naturalmente, não estamos interessados nos outros.
2. essa probabilidade é quase sempre diferente de zero.
Não é verdade. Se não for zero, é um erro de forma funcional.
3. Você já verificou a multicolinearidade? IMHO, se você eliminar a multicolinearidade, só resta uma variável. Você já identificou os fatores significativos?
O que são "fatores significativos" não entendo, mas, por favor, olhe para os coeficientes de correlação.
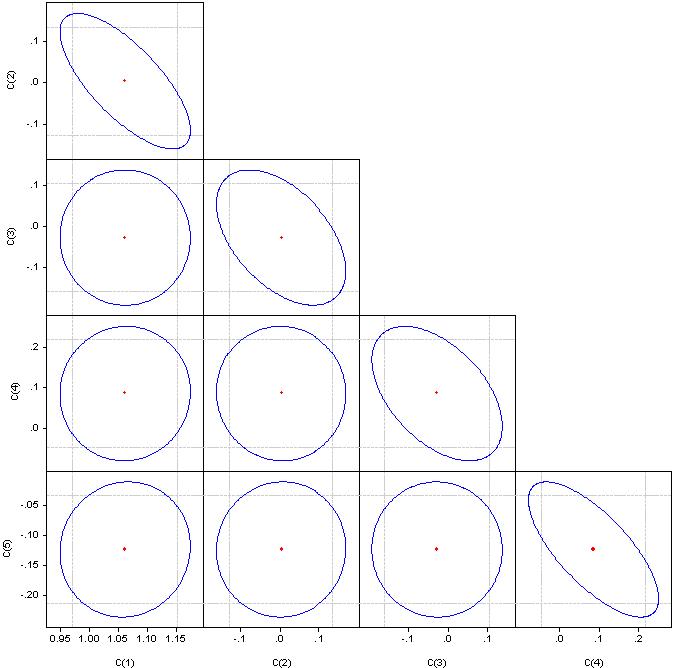
Se for um círculo, a correlação é zero. Se fundidos em uma linha reta, a correlação entre o par de coeficientes correspondentes é 100%.
4. Quantas observações você tem para 5 variáveis?
6736 observações
O primeiro passo em qualquer modelo de regressão é a seleção de fatores. Se você não aplicar regressão por etapas (com inclusões ou exceções), então você tem que selecioná-las manualmente.
Multicolinearidade - fechar dependência entre as variáveis do fator incluídas no modelo. Não a correlação dos coeficientes, mas a correlação dos fatores.
A presença de multicolinearidade leva a:
- distorção do valor de os parâmetros do modelo, que tendem a superestimar;
- fraco condicionamento do sistema de equações normais;
- complicação de o processo de determinação de as característicasmais significativas dofator .
Um indicador de multicolinearidade é que os coeficientes de correlação em pares excedem o valor de 0,8. A fim de eliminá-la, precisamos remover os fatores redundantes. Seja manualmente ou por regressão gradual.
Veja no pacote - regressão de degraus ou regressão de cumeeira.
E 6736/4 é um número excessivo de observações. Precisamos pesquisar no Google - não me lembro como determinar o número ideal de observações com base no número de fatores.
Tenha a gentileza de participar dos meus fios econométricos.
Vamos continuar com a seleção da literatura.
O próximo tópico é os atrasos de Almon.
Como observado acima, há dificuldades com coeficientes de regressão calculados usando o método dos mínimos quadrados. Uma idéia surgiu para impor restrições adicionais aos coeficientes de regressão nos quais a variável dependente é determinada por vários desfasamentos da variável independente, como na equação acima.
A idéia é impor restrições aos coeficientes nos valores de defasagem, de modo que obedeçam a alguma distribuição polinomial. EViews chama esta abordagem de "polinômios de atraso distribuído (PDL)". A escolha do grau particular de polinômio é determinada experimentalmente.
Esta abordagem é descrita aqui.
Aqui está um exemplo prático.
Vamos construir um análogo de uma escala com um período de 5, mas os coeficientes de barra devem estar em um polinômio de 3ª ordem.
Em EViews está escrito como se segue para EURUSD
EURUSD PDL(EURUSD(-1), 5,3)
De uma forma mais familiar:
EURUSD = + C(5)*EURUSD(-1) + C(6)*EURUSD(-2) + C(7)*EURUSD(-3) + C(8)*EURUSD(-4) + C(9)*EURUSD(-5) + C(10)*EURUSD(-6)
Estimamos os coeficientes por OLS e obtemos o resultado da estimativa do coeficiente:
EURUSD = + 0,934972661616*EURUSD(-1) + 0,139869148138*EURUSD(-2) - 0,093599954464*EURUSD(-3) - 0,0264992987207*EURUSD(-4) + 0,0801064628352*EURUSD(-5) - 0,0348473223286*EURUSD(-6)
As estatísticas sobre a estimativa da equação são as seguintes:
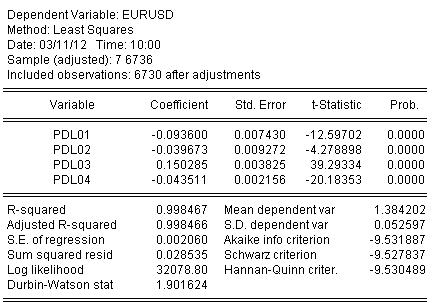
A partir das estatísticas podemos ver um nível muito bom de mapeamento do quociente inicial por nosso aceno de Almon R-quadrado = 0,998467
Em termos gráficos, parece que sim:

A regressão (ondulação de Almon) cobriu completamente o quociente original.
E uma última colher de mel.
Vamos ver qual é o resíduo, ou seja, a diferença entre o purê de nosso Almon e o cotier original. A estacionaridade/não estacionaridade deste resíduo é muito importante.

O teste de raiz da unidade afirma que o resíduo é estacionário.
Os mash-ups que usamos não têm este nível de ajuste ao quociente original e à propriedade de estacionaridade do erro de ajuste.
Eu gostaria de mover os elos de um fio vizinho.
Estes links estão relacionados com a área mais problemática - o prognóstico.
A primeira é um anexo. há uma lista de referências.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Se você pesquisar no Google a palavra "econometria", você receberá uma enorme lista de literatura, o que é difícil de entender mesmo para um especialista. Um livro diz uma coisa, outra - outra, a terceira - apenas uma compilação dos dois primeiros com algumas imprecisões. Mas a abordagem "dos livros" não combina a clareza da aplicação destes livros na prática. Não estou interessado em que os intelectuais caiam em disparates nerds.
Assim como outras listas de livros neste fórum, por exemplo, sobre estatística, proponho que coletivamente compilemos uma lista de livros didáticos, monografias, dissertações, artigos, recursos da Internet e pacotes de software que, na opinião dos participantes, são relevantes para a medição de dados econômicos - à econometria. Entretanto, não esqueçamos que a estatística matemática é a irmã mais velha da econometria. Sugiro não incluir nada relacionado à análise técnica nesta lista.
Para excluir o deslizamento para a botânica, proponho uma abordagem específica para a lista de livros. Postamos links (os próprios livros) somente se eu souber de software, que implementa algoritmos a partir destes livros. Reduzi para EViews. Este programa não tem vantagem sobre outros, tem vantagens e desvantagens, mas eu o tomo como uma rubrica para a econometria. Anexei a tabela do conteúdo do segundo volume do manual do usuário, a fim de delinear de uma só vez a mais ampla gama possível de problemas. Devido à abordagem proposta, várias áreas usadas em econometria, mas não incluídas em EVIEWS, por exemplo NS, wavelets, etc., estão excluídas. Naturalmente, referências a tais programas e livros também são bem-vindas.
Se pudermos não apenas fornecer um link para a fonte do algoritmo, mas também fazer cálculos específicos, este fio não terá valor.
Sugiro utilizar os números dos capítulos do anexo para o agrupamento de livros.
Portanto, favor apoiar.