Para o autor (sem apelido por algum motivo).
O mesmo problema pode ser resolvido de outras maneiras. Há testes para variáveis redundantes e ausentes. Eu poderia fazer isso e comparar com seus resultados. Mas preciso de todos os seus arquivos no formato .csv.
...Preciso de todos os seus arquivos no formato .csv.
Acho que a fonte está no arquivo masterdata.zip.
Artigo publicado Usando análise discriminante para criar sistemas de negociação:
Autor: ArtemGaleev
Depois de escolhermos as variáveis, teremos de estabelecer uma relação entre elas, na qual o preço será a variável dependente (função) e os outros indicadores serão as variáveis independentes. Aqui está a equação esquemática:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 significa o valor anterior. Isso é natural, pois o indicador é derivado do preço analiticamente. Vamos levar em conta que o preço é um incremento, portanto, usaremos os incrementos dos indicadores. Por preguiça, não considero todos os indicadores. Vamos estimar essa equação pelo método dos mínimos quadrados:
Obtivemos uma estimativa dos coeficientes da equação. A última coluna é muito interessante: ela significa a probabilidade de que o coeficiente correspondente seja igual a zero. Essa probabilidade para todos os coeficientes é muito maior do que pelo menos 10%, ou seja, podemos considerar que não podemos rejeitar a hipótese de que os coeficientes correspondentes sejam iguais a zero. Consequentemente, o R-quadrado tem um valor ridículo.
Concluo que é inútil lidar com a classificação dos indicadores - eles são inúteis porque não têm nada a ver com o incremento de preço.
Ou estou errado?
...Ou estou errado?
Acho que você está certo :-)
faa1947, tenho uma pergunta para você. Gostaria de esclarecer algumas coisas... Foi assim que calculei os dados de sua equação:
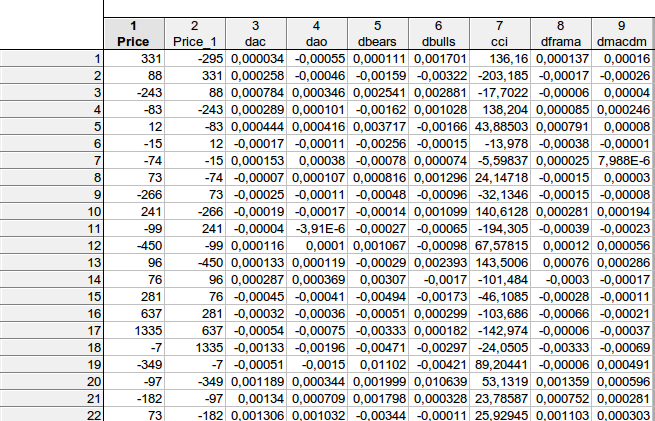
Os dados da tabela correspondem à sua equação esquemática price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
E obtive o seguinte resultado:
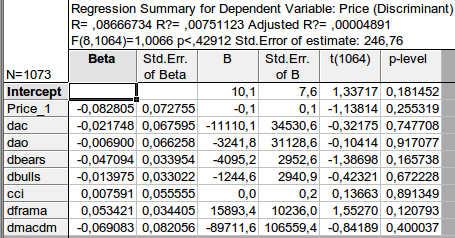
Depois de escolhermos as variáveis, teremos de estabelecer uma relação entre elas, na qual o preço será a variável dependente (função) e os outros indicadores serão as variáveis independentes. Aqui está uma equação esquemática:
price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 significa o valor anterior. Isso é natural, pois o indicador é derivado do preço analiticamente. Vamos levar em conta que o preço é um incremento, portanto, usaremos os incrementos dos indicadores. Por preguiça, não considero todos os indicadores. Vamos estimar essa equação pelo método dos mínimos quadrados:
Obtivemos uma estimativa dos coeficientes da equação. A última coluna é muito interessante: significa a probabilidade de que o coeficiente correspondente seja igual a zero. Essa probabilidade para todos os coeficientes é muito maior do que pelo menos 10%, ou seja, podemos considerar que não podemos rejeitar a hipótese de que os coeficientes correspondentes sejam iguais a zero. Consequentemente, o R-quadrado tem um valor ridículo.
Concluo que é inútil lidar com a classificação dos indicadores - eles são inúteis porque não têm nada a ver com o incremento de preço.
Ou estou errado?
Forneça o nome do método estatístico que você usou. Foi a construção de uma equação de regressão linear, em que a entrada são os indicadores e a saída é o preço futuro? Isso está correto? Isso não funcionará no forex, pois ele não é um sistema determinístico linear. A análise discriminante tem uma tarefa diferente, pois cria modelos para reconhecimento de padrões com base em descrições externas do sistema.
Se a classificação de indicadores para analisar os incrementos de preço fosse inútil, então a análise técnica não teria sentido. Felizmente, o preço não se comporta de forma caótica, ele tem uma memória de eventos anteriores.
Você parece estar certo :-)
faa1947, tenho uma pergunta para você. Gostaria de esclarecer algumas coisas... foi assim que calculei os dados de sua equação:
Os dados da tabela correspondem à sua equação esquemática price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
E obtive o seguinte resultado:
Os dados brutos têm a seguinte aparência:
As equações têm a seguinte aparência:
Equação de estimativa:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Coeficientes substituídos:
=========================
PRICE = -0.0228102658125*PRICE(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
Não entendo seu cálculo. Tenho o princípio de usar o valor de defasagem (valor anterior). Isso torna possível fazer uma previsão. Se a defasagem -1 corresponder à primeira observação, a variável dependente corresponderá a uma observação nova, prevista e não observada.
O que é nível p? Para mim, é a probabilidade de que o coeficiente correspondente seja zero.
Forneça o nome do método estatístico que você usou. Foi uma equação de regressão linear em que a entrada são os indicadores e a saída é o preço futuro? Isso está correto?
A regressão foi estimada usando o método dos mínimos quadrados. Ela pode ser usada para fazer previsões.
Isso não funcionará para o forex, pois ele não é um sistema determinístico linear.
Se for linear, será em um exemplo específico. Não é determinístico porque até mesmo os coeficientes são tratados como variáveis aleatórias. Todos os coeficientes não são calculados, mas estimados. A segunda coluna mostra o erro padrão da estimativa do coeficiente. Observe que ele é enorme.
Se a classificação dos indicadores para analisar os incrementos de preço fosse inútil, a análise técnica não teria sentido.
Exatamente isso, e ouso garantir que não sou o único que pensa assim. A AT não é uma ciência, mas um tipo de astrologia. Originalmente, há 300 anos, era um sistema para visualizar o kotir. Desde então, evoluiu enormemente. Todo o resto é para os Pinóquios no campo dos milagres. Fiquei feliz com seu artigo, pois ele tem um pensamento regular e repetível.
Se a classificação dos indicadores para analisar o incremento de preços fosse inútil, eu não teria feito nada.
Aqui analisamos um caso especial de indicadores. É sempre necessário provar que um determinado indicador ou seu uso tem algo a ver com uma cotação. A AT nunca considera essa questão.
Felizmente, o preço não se comporta de forma caótica, ele tem uma memória de eventos anteriores.
Toda a econometria é construída com base no pressuposto de que uma cotação tem um componente determinístico (autocorrelação, memória) e ruído.
A análise discriminante tem uma tarefa diferente: ela cria modelos para reconhecimento de padrões com base em descrições externas do sistema.
A tarefa é clara. Mas se o resultado obtido é confiável, essa é a questão. O problema não é a classificação (isso é parte do problema, que também precisa ser resolvido), mas a confiança na previsão resultante. Esse é exatamente o problema.
Não entendo seu cálculo. Meu princípio é usar o valor de defasagem (valor anterior). Isso torna possível fazer uma previsão. Se a defasagem -1 corresponder à primeira observação, a variável dependente corresponderá a uma observação nova, prevista e não observada.
O que é nível p? Para mim, é a probabilidade de que o coeficiente correspondente seja zero.
faa1947, forneci a tabela com defasagens (para as primeiras linhas - não consigo ajustar a tabela inteira). Mas primeiro calculei as diferenças de indicadores, de modo que o número total de linhas é 1073 em vez de 1074. Em seguida, movi a variável dependente Price um passo à frente.
Descobriu-se que, no exemplo da primeira linha:
331 = C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, desde que
PREÇO = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
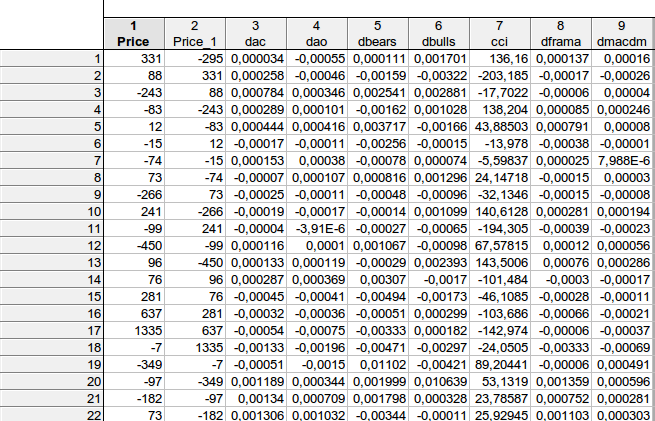
Em geral, obtive aproximadamente um resultado semelhante - não há como rejeitar a hipótese nula de que os coeficientes considerados são iguais a zero...
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Usando a Análise Discriminante para Desenvolver Sistemas de Negociação foi publicado:
Autor: ArtemGaleev