Discussão do artigo "Modelo de regressão universal para predição do preço do mercado" - página 8
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Entre em contato por mensagem privada e informe-se sobre as condições.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Os indicadores são pagos ou algo do gênero? Publicado na base de código, use-o como quiser!
Foi publicado o novo artigo Universal Regression Model for Market Price Prediction (Modelo de regressão universal para previsão de preços de mercado ):
Autor: Юсуфходжа
bom artigo.
muito impressionante
É uma pena, mas há erros logo no início do artigo.
Em primeiro lugar, o incremento de preço em algum momento t terá, obviamente, algum valor e nós o denotamos por D0. Vamos supor.
Em seguida... Agora, em t=0, entendo que não há impacto sobre o preço e, aparentemente, também não há incremento de preço decorrente do impacto externo. Entretanto, chamamos novamente o delta de D0.
Em seguida, colocamos dt/tau na fórmula, que é 1/C^2 de qualquer forma, ou seja, demos aceleração ao impacto, que moverá a regressão geométrica de qualquer forma. Por que deveríamos? Afinal de contas, ainda não definimos o que é esse impacto...
bem, em geral.
É uma pena, mas há erros logo no início do artigo.
Em primeiro lugar, o incremento de preço em algum momento t terá, obviamente, algum valor e nós o denotamos por D0. Vamos supor.
Em seguida... Agora, em t=0, entendo que não há impacto sobre o preço e, aparentemente, também não há incremento de preço decorrente do impacto externo. Entretanto, chamamos novamente o delta de D0.
Em seguida, colocamos dt/tau na fórmula, que é 1/C^2 de qualquer forma, ou seja, demos aceleração ao impacto, que moverá a regressão geométrica de qualquer forma. Por que deveríamos? Afinal de contas, ainda não definimos o que é esse impacto...
Bem, em geral...
1. Do não é o incremento de preço, mas o potencial inicial da força que afeta o preço no momento t=0.
2. do artigo: ".... pressupõe que o preço de mercado, que está em equilíbrio, pode mudar somente sob a ação de alguma força externa D(t), cuja magnitude e valor serão medidos na mesma dimensão do preço.
Vamos supor também que a mudança no preço de mercado P(t) com a passagem do tempo t desde o início da influência dessa força, aumentando continuamente a partir do valor zero por alguma regularidade que ainda desconhecemos, tende a atingir o valor P(∞) = D0 no infinito. Ou seja, por D0 entendemos um aumento ou uma redução finita do preço de mercado, dependendo da natureza e do sinal dessa força de influência.
Além disso, presumimos que D(t=0) = D0. Vamos supor ainda que, durante o período infinitesimal de tempo dt, a força de influência diminuirá no valor dD(t) em proporção à força restante D(t) no momento do tempo t:
Assim, obtemos a dependência exponencial de D(t) em relação ao tempo t na forma:
Onde: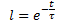
t - tempo desde o início do impacto da força desestabilizadora em unidades de série temporal, seg. (min, horas, dias, semanas, décadas, meses, anos);
τ (tau) - o coeficiente de proporcionalidade, numericamente igual à constante de tempo do processo, seg. (min, horas, dias, semanas, décadas, meses, anos)."
De onde você tirou a dimensionalidade de 1/s^2? Essa proporção não tem dimensionalidade. Eu não a inseri, eu levantei a hipótese de que a taxa de mudança (diminuição) de uma força atuando em um processo é proporcional à própria força, o que não contradiz a lógica, e então essa hipótese foi totalmente confirmada. Como coeficiente de proporcionalidade, introduziu a razão a (alfa) = 1/tau, que tem a dimensão inversa do tempo. Por a (alfa), entendo a impedância do sistema, ou seja, a resistência do sistema ao fluxo do processo, e tau é a imagem do tempo nas transformações de Laplace, como se verificou mais tarde, e permite levar a análise do processo do domínio diferencial para o domínio comum. Isso significa que qualquer processo tem seu próprio tempo, diferente do nosso, e o tau atua como um "tradutor" de tempos, se assim posso dizer. Nas entranhas do artigo, apresentei uma maneira de estimar o tau:
Agora, se os valores da função f para os momentos correspondentes do tempo t forem conhecidos, então, a partir dessa equação, os parâmetros n, τ e o coeficiente β são determinados da seguinte forma:
onde:
Os valores da função f para os momentos correspondentes do tempo t e do tempo t são determinados pelos valores reais do preço de mercado P0, P1,..., Pk para os momentos do tempo h0, h1,..., һk a partir do início de sua desestabilização por diferenciação numérica, referida ao meio do intervalo:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); e assim por diante;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; e assim por diante.