В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
Não há contradição aqui. A lei fundamental da oferta e demanda prevê esses efeitos. Este é o ponto: todo o modelo deve ser considerado dinamicamente, ou seja, os limites do canal fundamental horizontal mudam com o tempo. Para entender do que estou falando, é necessário primeiro considerar um modelo estático clássico de oferta e demanda (para o "aqui e agora"):
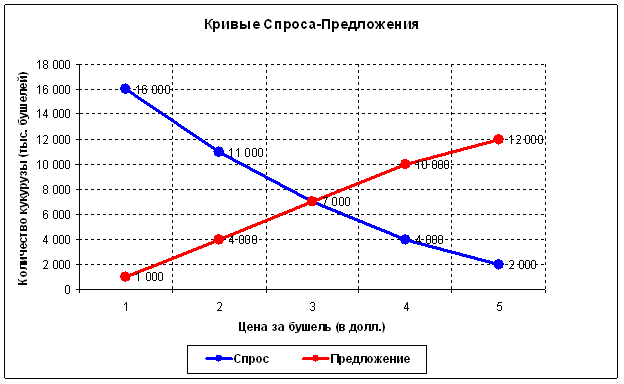
Ou seja, em cada momento, há apenas um ponto de troca maximamente eficiente de um bem (neste caso, 7.000 bushels a um preço de US$ 3). Em todos os outros pontos, menos mercadorias serão trocadas por menos dinheiro. A situação macroeconômica está em constante mudança, o que significa que esse ponto de troca eficiente também está mudando. Entretanto, o mercado é eficiente e sua principal tarefa é buscar constantemente esse ponto ou o próprio preço de equilíbrio ("todos que queriam comprar - compraram, todos que queriam vender - venderam"). O volume nesse ponto deve ser grande, porque nesse ponto a quantidade máxima de mercadorias é trocada. Leva tempo para o mercado realizar esse volume. Essa teoria prevê o efeito do acúmulo de volume:
O mercado está na maior parte do tempo na fase de consolidação (na área de sua eficiência máxima).
Entretanto, a economia mundial como um todo está em constante evolução. Surgem novas tecnologias, os padrões de vida melhoram. Consequentemente, por um lado, são necessários cada vez mais bens e serviços e, por outro lado, o progresso científico e tecnológico possibilita a produção de cada vez mais bens e serviços. A liquidez aumenta com o tempo. O volume dos mercados mundiais deve crescer e, como consequência, sua volatilidade aumenta e, portanto, o tamanho da crise entra em colapso. Como a demanda aumenta com o tempo, o preço sobe. Ao mesmo tempo, o progresso científico e tecnológico fornece a essa demanda cada vez mais bens e serviços. Consequentemente, o ponto de equilíbrio geralmente se deslocará para cima e para a direita ao longo do tempo. O mercado, que está sempre se movimentando em torno desse ponto, geralmente também cresce (tende a preços altos).

É daí que vem esse mesmo "efeito de tendência". Tudo isso se encaixa tão bem nos cálculos matemáticos que é simplesmente impressionante. De qualquer forma, os efeitos econômicos devem explicar as dependências matemáticas, mas não o contrário.
Há uma imprecisão no artigo: se tomarmos um marinheiro bêbado como analogia, o tamanho do degrau será diferente. Em termos gerais, um passo tem 80 cm de comprimento se estiver saindo do bar, e um passo para trás (para o bar) tem 60 cm. A tendência é a mesma, e também é sabido que o movimento descendente do mercado é mais rápido do que o movimento ascendente. E, no artigo, todos os passos são os mesmos +1 ou -1.
Portanto, esse modelo não pode ser considerado adequado. É apenas uma moeda, cujas propriedades de distribuição são conhecidas e estudadas há muito tempo.
há uma imprecisão no artigo: se tomarmos o marinheiro bêbado como analogia, então o tamanho do degrau é diferente. A grosso modo, um passo tem 80 cm de comprimento se estiver saindo do bar, e um passo para trás (para o bar) tem 60 cm. A tendência é a mesma, e também é sabido que o movimento descendente do mercado é mais rápido do que o movimento ascendente. E no artigo, todos os passos são iguais, +1 ou -1".
A moeda tem um análogo contínuo - o modelo de movimento browniano geométrico. Ele é descrito aqui http://algoritmus.ru/?p=2889.
"Stochastic approach to solving problems of algorithmic trading" (Abordagem estocástica para resolver problemas de negociação algorítmica).
Autores: Arsen Yakovlev, Grigory Franguridi
Publicado: Revista "D-Shtrich" nº 16/6 de setembro de 2010
Este artigo tem as mesmas ideias do meu artigo, apenas mais matemática. O fato de usar um modelo discreto ou contínuo é uma questão de gosto. Eles são iguais. Apenas um modelo tem integrais e o outro tem somas. E o modelo de moeda já é compreendido por crianças em idade escolar, enquanto o modelo contínuo é compreendido apenas por estudantes.
"Também é sabido que o movimento descendente do mercado é mais rápido do que o movimento ascendente" - isso é muito interessante para mim - você pode me fornecer um link para a pesquisa/artigo - eu preciso dele para a autoeducação.
"Portanto, esse modelo não pode ser considerado adequado de forma alguma. É apenas uma moeda cujas propriedades de distribuição são conhecidas e estudadas há muito tempo." - Nenhum modelo descreve adequadamente a realidade em 100%. Incluindo a taxa da moeda como um modelo de mercado. É por isso que tivemos que inventar um modelo de uma moeda com uma tendência para ser mais adequado ao mercado.
- 2010.09.13
- val
- algoritmus.ru
Por que uma moeda, exatamente? Ela tem dois lados - o que eles refletem? Apenas um passeio aleatório ideal em uma linha reta (análogo - para cima, para baixo), ou seja, unidimensional. O preço pode ter outro estado - plano, ou seja, já é uma moeda com três lados, ou seja, temos um passeio aleatório bidimensional. A partir dos gráficos acima, podemos ver que esse estado de mercado praticamente não é modelado - não podemos ver um flat rígido.
A curva amarela na Figura 2 é a mais próxima de um plano. O plano mais apertado será obtido se usarmos o parâmetro a=-0,5. Então, obteremos uma linha horizontal +1 -1 +1 -1 -1 -1 +1 -1 -1 ..... Portanto, dois lados da moeda são suficientes para descrever um plano. A propósito, "flat", nos termos do artigo, é chamado de "anti-tendência".
Mas, nesse caso, todo o gráfico se tornará mais horizontal, se eu entendi corretamente, e no mercado real pode haver tanto uma tendência acentuada quanto uma estabilidade rígida, ou seja, esses fenômenos são independentes. A independência é a necessidade de um terceiro lado da moeda. Simplesmente, o mercado está vagando no plano, porque o fator tempo vagueia, e a moeda tem um modelo unidimensional de vagueio, e uma simples (sem vagueio) varredura desse modelo para o tempo não é muito correta. Mas, apesar disso, esse artigo é muito útil.
No modelo de moeda com uma tendência, a tendência é considerada constante durante toda a vida útil do mercado. E, como mostra o indicador de tendência da taxa real, a tendência está mudando constantemente. E somente em média, em um longo período de tempo (anos), a tendência é medida como uma constante.
Para fazer com que o modelo "taxa de moeda com tendência" corresponda ao mercado, você pode complicá-lo. O parâmetro "a" pode se tornar caoticamente dependente do tempo ou outra coisa pode ser inventada. É uma questão de criatividade. A rigor, não há necessidade de introduzir uma segunda dimensão, mas se você quiser, pode adicionar um segundo multiplicador caótico ao lado de "a".
É necessário um modelo simples com uma tendência constante para testar, por exemplo, esse indicador New Moving Mini-Max technical analysis indicator e sua implementação em MQL5. Não é realista lidar com esse indicador no curso real, mas seria bom testá-lo em um modelo simples com uma tendência constante.
...O fato de usar um modelo discreto ou contínuo é uma questão de gosto. Eles são iguais. Apenas um modelo tem integrais e o outro somas. E o modelo de moeda já é compreendido por crianças em idade escolar, e o modelo contínuo apenas por estudantes...
É aí que está o erro.
1. A transição do modelo contínuo para o modelo discreto deve ser feita corretamente.
2. ambos os modelos podem ser os mesmos (contínuo e discreto), mas é necessário cumprir a condição: a etapa em + e em - deve ser a mesma. Sua magnitude.
3. levou barras para analisar que sua afirmação seria verdadeira: "Eles são iguais. Apenas um modelo tem integrais e o outro tem somas." Prove que todas as barras são iguais. Você pode provar isso?
4. somente um gráfico tem essa propriedade, o gráfico renko... você pode substituí-lo por +1 -1(https://www.mql5.com/pt/code/9447#25419).
Obrigado pelo link do artigo. Eu o li. Ele sugere o uso do modelo ARFIMA, seu passeio aleatório. Esses são modelos diferentes. Seria interessante ler o artigo a seguir, tanto o seu quanto o do autor. Nele é provado que seus modelos de mercado propostos são adequados. Não apenas afirmado em palavras, mas provado matematicamente ... e dado o cálculo desse número ...
H.Y. Muitas pessoas entendem essa bela palavra adequação, mas nem mesmo sabem como calculá-la. Você escreveu em sua postagem que não existe um modelo 100% adequado. Concordo plenamente com você. A questão é o quanto o modelo proposto é adequado ao mercado em 20, 30 ou 99,999999999%....
Tente modelar uma pilha, a pilha tem uma estrutura clara, a pilha vê ordens para um determinado número de pontos para cima e para baixo.
O gerador passa por todas as células (pode não ser +1 -1, mas a geração de volumes aleatórios) e, depois que todas as células da pilha passam pelo gerador, é feito o cálculo de para onde mover o ponto central da pilha.
E não se esqueça de reiniciar o SRAND depois de gerar 32768 rand, caso contrário, sua sequência será repetida.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Caminhada aleatória e indicador de tendência foi publicado:
A caminhada aleatória parece muito similar com os dados de mercado reais, mas possui alguns recursos significativos. Neste artigo, considerarei as propriedades da Caminhada Aleatória, simulada usando o jogo de cara e coroa. Para estudar as propriedades dos dados, foi desenvolvido o indicador de modismo.
Autor: Гребенев Вячеслав