Denis, ho questo commento da fare sull'articolo.
Per quanto riguarda la teoria, non ci sono domande, tutto è presentato in dettaglio.
Per quanto riguarda la pratica, vorrei attirare la vostra attenzione sulle figure in cui mostrate gli istogrammi empirici, in particolare la Figura 2. Il punto è che avete commesso due imprecisioni molto significative nella vostra analisi.
In primo luogo, avete impostato un numero troppo basso di classi per lo script che genera gli istogrammi - solo 9, il che di per sé è un colpo enorme alla potenza del criterio di Pearson e rende la sua applicazione inefficace. Per il futuro, prendete 200-300 classi per essere sicuri che, se la dimensione del campione lo consente (e lo consente), non commetterete errori. Se aveste fatto esattamente così, sareste stati in grado di assicurarvi che il test per la distribuzione lognormale avrebbe dato un risultato negativo, così come il test dei rendimenti per gli ipersecani. Tra l'altro, è molto facile assicurarsi che due distribuzioni di questo tipo non possano rappresentare contemporaneamente un certo valore e il suo modulo, basta prendere la "metà" dell'ipersecondo e convolgerla con se stessa (analogamente a come si prende il modulo da una variabile casuale): sicuramente non si otterrà una lognormale.
La seconda imprecisione è che non avete utilizzato la conoscenza a priori che il vertice (alias aspettativa) della distribuzione dei rendimenti deve essere esattamente a 0 (altrimenti saremmo tutti miliardari da tempo). Ecco perché l'istogramma della Figura 2 appare spostato verso destra, anche se non dovrebbe. Anche in questo caso, tenerne conto quando si traccia l'istogramma renderebbe i test più affidabili.
P.S. Sto scrivendo un articolo sulle basi della modellazione, da cui l'interesse così vivo. Grazie per il tuo articolo, è nell'argomento. Saluti.
...In primo luogo, avete impostato un numero troppo piccolo di classi per lo script che genera gli istogrammi - solo 9, il che di per sé è un duro colpo per la potenza del criterio di Pearson e rende la sua applicazione inefficace. Per il futuro, prendete 200-300 classi per essere sicuri; naturalmente, se la dimensione del campione lo consente (e lo consente), non commetterete errori. Se aveste fatto così, sareste stati in grado di assicurarvi che il test per la distribuzione lognormale avrebbe dato un risultato negativo, così come il test dei rendimenti per gli ipersecani. Tra l'altro, è molto semplice assicurarsi che due distribuzioni di questo tipo non possano rappresentare contemporaneamente un certo valore e il suo modulo, basta prendere la "metà" dell'ipersecondo e convolgerla con se stessa (analogamente a come si prende il modulo di un valore casuale): sicuramente non si otterrà una lognormale.
Caro alsu, grazie per la tua opinione!
Andiamo con ordine.
Il numero di classi non viene stabilito volontariamente, ma in base a una formula. Nel mio caso si tratta della formula di Sturgis. È una delle regole più diffuse. Non è perfetta, su questo sono d'accordo. Ma comunque...
E tu prendi 200-300 classi secondo quale regola?
La seconda imprecisione è che non hai usato la conoscenza a priori che il top (alias aspettativa) della distribuzione dei rendimenti deve essere esattamente a 0 (altrimenti saremmo tutti miliardari da tempo). Ecco perché l'istogramma della Figura 2 appare spostato verso destra, anche se non dovrebbe. Anche in questo caso, tenere conto di questo punto nella costruzione dell'istogramma renderebbe i test più affidabili.
Analizzo il campione su base fattuale. Analizzo ciò che ho. E su quale base il vertice della distribuzione dei rendimenti dovrebbe trovarsi esattamente nel punto 0? Forse sto fraintendendo qualcosa...
Inoltre, se si guarda alla distribuzione a cui è stato applicato il fitting (che era X~HS(-0.00, 1.00)), è facile vedere che il primo parametro - il parametro di spostamento - è esattamente 0. In effetti, è uguale al parametro di spostamento. Infatti, è uguale all'aspettativa.
Ecco un'altra relazione html sul campionamento dei valori standard. Spero che la figura sia più o meno leggibile. Ma non è identica a quella dell'articolo. Ho preso i dati più recenti proprio ora.
Come potete vedere, media =0. La distribuzione migliore è quella della secante iperbolica: X~HS(0.00, 1.00).
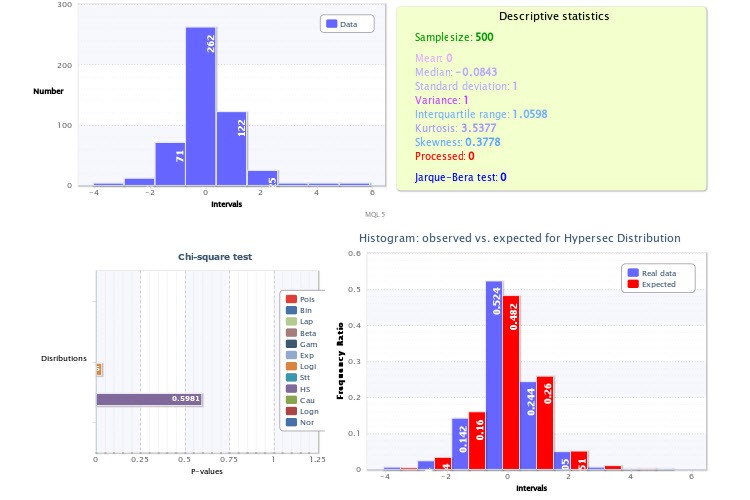
Esattamente, la formula di Sturges ha dato esattamente 9 classi, ma questo è piuttosto un motivo per pensare di aumentare la dimensione del campione (invertendo la formula, vedo che l'hai intorno a 256?).
Inoltre, questa formula funziona bene solo per popolazioni generali dalla distribuzione normale (per la quale è stata derivata) e, per come è considerata, la dimensione del campione non è superiore a 200 valori. È possibile utilizzare formule alternative - Diakonis, Scott....
In generale, Sturges non ha mai fornito una giustificazione logica della sua formula - sì, si basa sull'approssimazione della distribuzione normale con la distribuzione binomiale, e allora? Come può questo influire sulla questione dell'efficienza della scelta del numero di classi? Il criterio di ottimalità non è mai stato definito dall'autore e la formula stessa è stata scritta a caso. Ma il punto è che per molto tempo l'approccio di Sturges è stato l'unico ad essere formalizzato in qualche modo, ed è stato automaticamente (e, a mio parere, abbastanza sconsideratamente!) incluso in tutti i pacchetti statistici, il che, tra l'altro, è piuttosto fastidioso proprio perché questa formula fornisce quasi sempre un numero di classi estremamente sottostimato.
Anche in questo caso, esistono formule alternative, ma è la presenza di un personal computer, paradossalmente, a dare la possibilità di utilizzare la propria testa come un dispositivo, cioè un modo visivo per determinare il numero più o meno ottimale di classi per quel particolare campione, quando, modificando in modo fluido questo indicatore, si raggiunge un compromesso tra la scorrevolezza del grafico e la risoluzione dell'istogramma. Tra l'altro, questo metodo è spesso migliore e più veloce di qualsiasi formula.
Dico sempre a tutti: prima di inserire numeri nelle formule, chiedetevi cosa significa e come (e se) applicarli. In breve, sono contrario all'uso della formula di Sturges, che considero superata e inadeguata).
Per quanto riguarda la media. L'aspettativa dei rendimenti dovrebbe essere a 0 perché se così non fosse, potremmo stupidamente scommettere sempre in una direzione, corrispondente al segno di questo MO, e avere la garanzia di ottenere un rendimento di qualsiasi entità predeterminata. Ebbene, il vertice dovrebbe coincidere con il MO solo per ragioni di simmetria: la metà sinistra del grafico dovrebbe essere l'immagine speculare di quella destra (l'aumento e la diminuzione del tasso sono statisticamente uguali e non dovrebbero esserci differenze tra loro), quindi il centro di simmetria coincide con il centro.
Poiché prendete HS(0.00, 1.00), quindi, dovreste centrare le classi - cioè la classe zero dovrebbe includere i valori dell'indice in un intervallo simmetrico (-x0;x0), altrimenti introduciamo nei calcoli un errore sistematico associato allo spostamento delle classi rispetto allo zero, che alla fine si insinua nel risultato del test chi^2. Il punto 0 non si trova al centro della classe zero.
In effetti, la questione di come rendere simmetriche le classi su dati discreti è abbastanza non banale e, ancora una volta, è bene risolverla per ogni particolare campione individualmente e con molta attenzione, altrimenti si rischia di ottenere risultati inadeguati anche a causa della scelta sbagliata dei confini della divisione in classi.
Mi piace la sua opinione sull'applicabilità delle conoscenze scientifiche nel trading.
Potrebbe dirmi quali libri consiglierebbe a una persona che conosce la teoria delle probabilità e la statistica matematica?
Denis, buon pomeriggio.
Mi piace la sua opinione sull'applicabilità delle conoscenze scientifiche nel trading.
Per favore, mi dica quali libri consiglierebbe a una persona che ha familiarità con la teoria delle probabilità e la statistica matematica.
Grazie per la sua opinione!
Penso che si debba cercare qualcosa per i principianti, quindi, qualche libro di ruolo. L'importante è che il testo del libro non scoraggi la lettura ulteriore :-))).
Mi è piaciuto qualcosa di Gaidyshev e qualcosa di Bulashev.....
C'è un thread interessantequi.
- rsdn.org
La seconda imprecisione è che non avete utilizzato la conoscenza a priori che il vertice (ovvero l'aspettativa) della distribuzione dei rendimenti deve essere esattamente a 0 (altrimenti saremmo tutti miliardari da tempo).
Non è affatto così. Uno spostamento del vertice della distribuzione rispetto allo 0 (crescita/declino di uno strumento) non significa che sarà lo stesso in futuro. Ecco perché la maggior parte dei trader non sono miliardari, non perché.
Saluti.
...Lo spostamento della parte superiore della distribuzione rispetto allo 0 (strumento in ascesa/caduta) non significa necessariamente che questo sarà il caso in futuro...
Concordo.
Domanda per Alsu. Quando parla di punto zero si riferisce all'efficienza del mercato?
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Il ruolo delle distribuzioni statistiche nel lavoro del trader è stato pubblicato:
Questo articolo è una continuazione logica del mio articolo Statistical Probability Distributions in MQL5 che espone le classi per lavorare con alcune distribuzioni statistiche teoriche. Ora che abbiamo una base teorica, suggerisco di procedere direttamente a set di dati reali e provare a fare un uso informativo di questa base.
In generale, la generazione della distribuzione specificata ha avuto successo.
Ho anche scritto lo script fitAll.mq5 che funziona in modo simile allo script randomTest.mq5. L'unica differenza è che il primo ha la funzione fitDistributions. Ho impostato il seguente compito: adattare tutte le distribuzioni disponibilia un campione di variabili casuali ed eseguire un test statistico.
Non è sempre possibile adattare una distribuzione a un campione a causa della mancata corrispondenza dei parametri che porta alla comparsa di righe nel Terminal, le quali informano che la stima non è possibile, ad es. "La distribuzione beta non può essere stimata!".
Inoltre, ho deciso che questo script dovrebbe visualizzare i risultati statistici sotto forma di un piccolo report HTML, un esempio del quale può essere trovato nell'articolo "Charts and Diagrams in HTML" (Fig.8).
Autore: Denis Kirichenko