
An Introduction to Fuzzy Logic
Introduction
The mathematical theory of fuzzy sets and fuzzy logic itself originated back in 1965. Its founding father was a Professor Lotfi Zadeh from the University of Berkeley, who first introduced both concepts in his article "Fuzzy Sets" in the Information and Control journal. This mathematical instrument allowed to introduce fuzzy concepts, that anyone could use, to exact science like mathematics, and laid the foundation for fundamentally new methods of problem solving on the basis of soft computing. All these innovations, when utilized properly, can greatly facilitate the process of solving classification problems, creating expert systems as well as building neural networks.
However, the practical application of fuzzy logic did not just stop there, in fact, this mathematical instrument has become predominantly used in automatic control theory. This can be further linked to the emergence of another new concept — fuzzy model, which is a particular case of a mathematical model.
1. Theory Behind Fuzzy Sets and Fuzzy Logic
In a certain way, a new theory of Lotfi Zadeh expands boundaries of mathematical logic and set theory familiar to us. Mathematical logic is capable of operating only with strictly formalized data, and object's membership to a particular set is defined only by two concepts, therefore, the term "membership" holds a discrete value that can have two meanings:
- "1" — if the object belongs to a set;
- "0" — if the object doesn't belong to a set.
In his fuzzy set theory Lotfi Zadeh shifted from discrete concepts of "membership" and introduced a new term — "degree of membership", whereas previously used term "set" was replaced by a "fuzzy set".
1.1. Basic Terms and Definitions
Definition 1. Fuzzy set ![]() on the universal set
on the universal set ![]() is a set of pairs
is a set of pairs ![]() , where
, where ![]() shows element's membership degree
shows element's membership degree ![]() to fuzzy sets.
to fuzzy sets.
Definition 2. Degree of membership is a number within range [0, 1]. The higher the degree of membership, the more the element of a universal set corresponds to the properties of a fuzzy set. Thus, if the degree of membership equals 0, then the given element does not correspond to the set, and on the contrary, if the degree equals 1, it becomes fully correspondent. These two cases are marginal, and without other options would be referred to a regular set. The presence of all other options is a key difference of a fuzzy set.
Definition 3. Membership function is a function that allows to calculate the membership degree of a random element of the universal set to a fuzzy set. Consequently, the domains of the membership functions should be within range [0, 1]. In most cases, the membership function is a continuous monotonic function.
Definition 4. Linguistic variable is a variable whose values are words or word combinations in a natural or artificial language. Fuzzy sets in particular are composed from linguistic variables. When defining a fuzzy set, the amount and nature of fuzzy variables are subjective for each individual task.
Definition 5. Term set is a set of all possible values, which a linguistic variable is capable of receiving.
Definition 6. Term can be any element of a term-set. In fuzzy set theory a term is formalized by a fuzzy set via the membership function. The membership function for each term is very individual and often unique. The methods of constructing these functions can be various: direct, indirect and relative frequencies. These are often based on the specific points of the membership function and the empirical evidence of an expert in this field.
Example:
Let's define a linguistic variable called "Age". By definition, "Age" is a period, a step towards development and growth of a human, animal, plant. The minimum value of this variable is 0, which means that a man is not even a year old. As a maximum value 80 is set up. Depending on the person's age we can give him the following assessment: "newborn", "young", "middle-aged", "old", "senior" etc. This list can accommodate a fairly large number of items. It will be a term set for our linguistic variable and its elements will be terms.
The figure below shows an example of the fuzzy variable "Age", which has only three terms set up: "Young," "Middle-aged,","Old." Each of these terms has its own membership function.
We will look into the case when someone is 30 years old, that on the figure will correspond with the perpendicular drawn from the point (30, 0). This line will cross all three membership functions in the following points:
- (30, 0) - the point of intersection of the graph "Age 30" and the graph "Old".
- (30, 0.29) - the point of intersection of the graph "Age 30" and the graph "Middle-aged".
- (30, 0.027) - the point of intersection of the graph "Age 30" and the graph "Young."
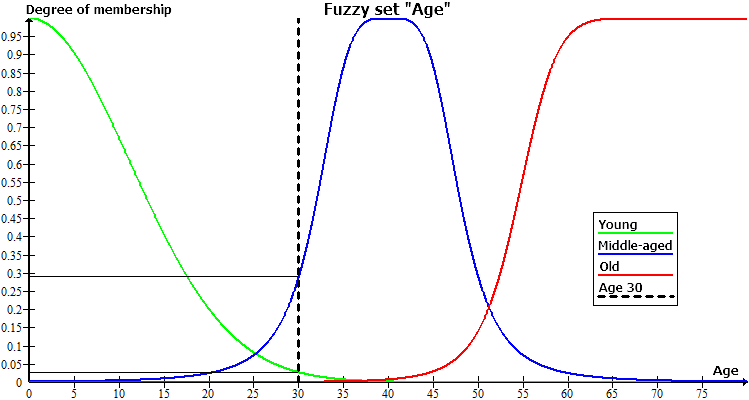
From the coordinates of these three points we can make a conclusion that a 30 year old man cannot be called old, and if choosing from the terms young and middle-aged, the second one would prevail. The degree of membership to the term "Middle-aged" equals 0.29, which is rather small, and in fact, for a 30 year old man another term "Young" would fit considerably better.
Definition 7. Defuzzification is a procedure of converting a fuzzy set into a specific number. Currently there are more than twenty methods available, and their results are significantly different from each other. Please note that so far the best results are achieved using the center of gravity defuzzification method.
1.2. Fuzzy Logic
Fuzzy logic — is a synthesis of the traditional Aristotelian logic when truth is marked as a linguistic variable. Fuzzy logic, equivalent to classical logic, has its own fuzzy logic operations on fuzzy sets defined. There are the same operations for fuzzy sets as well as for ordinary sets, only their calculation is by far more difficult. We should also note that the composition of fuzzy sets constitutes as a fuzzy set.
The main principles of fuzzy logic, setting it apart from classical logic, are the maximum proximity to the reflection of reality and a high level of subjectivity, which can lead to significant errors with calculation.
Fuzzy model — is a mathematical model whose calculation is based on fuzzy logic. Construction of such models is applicable when the subject of study has a weak formalization and its exact mathematical description is too complex or simply not known. The quality of these models' output values (error model) directly depends only on the expert, who set up this model. The best option to minimize errors is to draw the most complete and comprehensive model and subsequently adjust it with machine learning on a large training set.
The progress of a model construction can be divided into three main stages:
- Definition of input and output characteristics of a model.
- Building a knowledge base.
- Selecting one of the methods of fuzzy inference.
The first stage directly affects the consequent two and determines the future operation of the model. A knowledge base or, as sometimes called, rule base — is a set of fuzzy rules type: "if, then" that define the relationship between inputs and outputs of the examined object. The number of rules in the system is not limited and is also determined by the expert. The generalized format of fuzzy rules is as follows:
If rule condition, then rule conclusion.
Rule condition describes the current state of the object, and rule conclusion — how this condition affects the object. General view of conditions and conclusions cannot be selected because they are determined by a fuzzy inference.
Each rule in the system has its weight — this characteristic defines the importance of a rule in the model. Weighting factors are assigned to a rule within range [0, 1]. In many examples with fuzzy models, which can be found in the relevant literature, weight data is not specified, but it does not mean that it is not present. In fact, in such case for each rule from the rule base, the weight is fixed and equals 1. There can be two types of terms and conclusions for each rule:
- simple — includes one fuzzy variable;
- complex — includes several fuzzy variables.
Depending on the created knowledge base, the system of fuzzy inference is determined for a model. Fuzzy logical inference is a receipt of conclusion in form of a fuzzy set corresponding to the current value of the inputs with use of knowledge base and fuzzy operations. The two main types of fuzzy inference are Mamdani and Sugeno methods.
1.3. Mamdani-type Fuzzy Inference
According to the Mamdani's algorithm, fuzzy inference is executed using the fuzzy knowledge base:
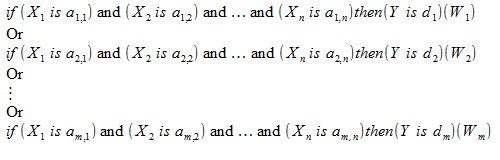
The values of input and output variables in the knowledge base are set up by fuzzy sets.
This knowledge base can be also written as:
![]()
where the following applies:
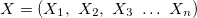 — vector of input variables;
— vector of input variables; — output variable;
— output variable;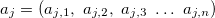 — vector of input variables in j-th rule, j = 0,1,2 ... m;
— vector of input variables in j-th rule, j = 0,1,2 ... m;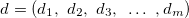 — vector of values for output variable;
— vector of values for output variable;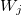 — weight of j-th rule, j = 0,1,2 ... m.
— weight of j-th rule, j = 0,1,2 ... m.
Let's introduce a new designation: ![]() — the membership function of fuzzy input or output variable v to fuzzy terms t.
— the membership function of fuzzy input or output variable v to fuzzy terms t.
The membership degree of input vector to fuzzy terms ![]() is calculated from the knowledge base as follows:
is calculated from the knowledge base as follows:
![]() — this function will characterize the work result of j-th rule from the knowledge base;
— this function will characterize the work result of j-th rule from the knowledge base;
where ![]() — s-norm (t-norm) operation, i.e. from plurality of implementations of OR (AND) logical operation. The following implementations are most frequently used: for operation OR — finding maximum and for operations AND — finding minimum.
— s-norm (t-norm) operation, i.e. from plurality of implementations of OR (AND) logical operation. The following implementations are most frequently used: for operation OR — finding maximum and for operations AND — finding minimum.
After finding ![]() for
for ![]() we will get m new membership functions, which altogether will form a new fuzzy set, denote it
we will get m new membership functions, which altogether will form a new fuzzy set, denote it ![]() , corresponding to the input vector
, corresponding to the input vector ![]() .
.
![]()
A special feature of this fuzzy set is that its universal set is a term-set of output variable ![]() .
.
Then, the following is needed:
- "cut" the membership function
 at level
at level 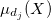 ;
; - combine the fuzzy sets.
In other words, by using the terms of fuzzy logic to produce an implication and aggregation of conditions. There are two ways to model the implication: finding the minimum or product of sets, aggregation — finding the maximum or sum of sets.
After that we will get the resulting fuzzy set, whose defuzzification will give us the exact system output.
1.4. Sugeno-type Fuzzy Inference
According to the Sugeno-type algorithm, fuzzy inference is executed by the fuzzy knowledge base:
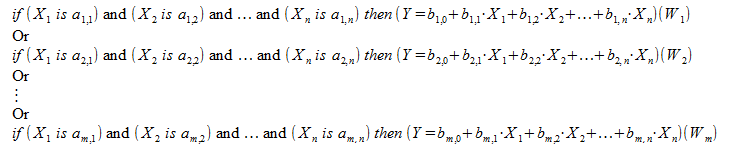
The Sugeno knowledge base is similar to the knowledge base of Mamdani except concluding rules ![]() , which are not defined by the fuzzy terms, but a linear function from the inputs:
, which are not defined by the fuzzy terms, but a linear function from the inputs:
![]()
Rules in the Sugeno knowledge base can be referred to a certain switch from one linear law "input - output" to the other, also linear. The boundaries of the subdomains are blurred, hence multiple linear laws of various degrees can be simultaneously executed.
This knowledge base can be also written as:
![]()
where the following applies:
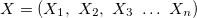 — vector of input variables.
— vector of input variables.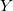 — output variable.
— output variable.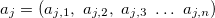 — vector of input variables in j-th rule, j = 0,1,2 ... m.
— vector of input variables in j-th rule, j = 0,1,2 ... m.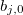 — coefficient of free term in the linear function for output value in j-th rule, j = 0,1,2 ... m.
— coefficient of free term in the linear function for output value in j-th rule, j = 0,1,2 ... m.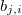 — coefficient of i-th term if the linear function for output value in j-th rule, j = 0,1,2 ... m, i = 0,1,2 ... n.
— coefficient of i-th term if the linear function for output value in j-th rule, j = 0,1,2 ... m, i = 0,1,2 ... n.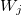 — weight of j-th rule, j = 0,1,2 ... m.
— weight of j-th rule, j = 0,1,2 ... m.
Let's introduce a new designation: ![]() — the membership function of fuzzy input or output variable v to fuzzy terms t.
— the membership function of fuzzy input or output variable v to fuzzy terms t.
The membership degree of input vector to fuzzy terms ![]() is calculated from the knowledge base as follows:
is calculated from the knowledge base as follows:
![]() — this function will characterize the work result of j-th rule from the knowledge base;
— this function will characterize the work result of j-th rule from the knowledge base;
where ![]() — s-norm (t-norm) operation, i.e. from plurality of implementations of OR (AND) logical operation. In the Sugeno fuzzy inference the following implementation of triangular norms are most frequently used: probabilistic OR as s-norm and production as t-norm.
— s-norm (t-norm) operation, i.e. from plurality of implementations of OR (AND) logical operation. In the Sugeno fuzzy inference the following implementation of triangular norms are most frequently used: probabilistic OR as s-norm and production as t-norm.
After finding ![]() for
for ![]() we will get m new membership functions, which altogether will form a new fuzzy set, denote it
we will get m new membership functions, which altogether will form a new fuzzy set, denote it ![]() , corresponding to the input vector
, corresponding to the input vector ![]() .
.
![]()
Please note that in contrast to the result of Mamdani's output, the above mentioned fuzzy set is the usual fuzzy set of the first order. It is based on the set of precise numbers. The resulting output value ![]() is defined as a superposition of linear dependencies performed at the given point
is defined as a superposition of linear dependencies performed at the given point ![]() in n-dimensional factor space. For this reason a fuzzy set
in n-dimensional factor space. For this reason a fuzzy set ![]() is defuzzified, calculating weighted average or weighted sum.
is defuzzified, calculating weighted average or weighted sum.
2. Fuzzy Logic Library FuzzyNet
In practice, the creation and operation process can be a difficult task even with a very simple fuzzy model involved. However, there are many different software tools and libraries, which can greatly simplify it. As an example, we will look into test scripts from the FuzzyNet library for MQL5 on how to create and operate with two fuzzy models.
2.1. Designing Mamdani-type Systems
The first example is a script Tips_Sample_Mamdani.mq5 from the FuzzyNet library for MQL5. It implements a fuzzy model for calculating tips, which a visitor prefers to leave based on his/her assessment of the service and food quality. This system has two fuzzy logic inputs, one output, the knowledge base consisting of three rules and the system of logical output of Mamdani-type.
The input parameters are fuzzy variables food and service, both variables are measured on a scale from 0 to 10 — these are their minimum and maximum values. The variable "food" consists of two terms: "rancid", "delicious". The variable "service" will consist of three fuzzy terms: poor, good, excellent.
Оn the output we get the fuzzy variable "tips". We will define a range of values for tips from 5% to 30% from the amount of the bill and introduce three terms: "cheap", "average", "generous" for this variable.
The knowledge base of the system will contain three rules:
- If (the service is poor) or (the food is rancid), then the tips are cheap.
- If (the service is good), then the tips are average.
- If (the service is excellent) or (the food is delicious), then the tips are generous.
Now that we have a general idea about the system, we shall look into the process of its creation:
- We will include the file MamdaniFuzzySystem.mqh from the FuzzyNet for MQL5 library:
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>This file allows you to create Mamdani-type systems and operate with them. - Now we can create an empty Mamdani system and fill it in:
MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem(); - We will create the first input variable "service". When creating fuzzy variables as a parameter for the constructor, first, the name of a variable is indicated in the line, followed by its minimum and maximum value.
FuzzyVariable *fvService=new FuzzyVariable("service",0.0,10.0);
- We add fuzzy terms to it. The fuzzy terms constructor uses names in the string as a first parameter and their corresponding membership function as a second parameter.
fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5.0, 0.0, 5.0))); fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5.0, 10.0, 15.0)));
In this example membership functions are presented as a triangular function for all the terms. - Now the already formed fuzzy variable is added to our system:
fsTips.Input().Add(fvService);
- Similarly, we are implementing a second input for the variable "food", but the terms for this variable will have a trapezoidal membership function.
FuzzyVariable *fvFood=new FuzzyVariable("food",0.0,10.0); fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0.0, 0.0, 1.0, 3.0))); fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7.0, 9.0, 10.0, 10.0))); fsTips.Input().Add(fvFood);
- Since the system has a Mamdani inference, its input and output values will be determined by the same methods. Therefore, in the same manner we create a similar output:
FuzzyVariable *fvTips=new FuzzyVariable("tips",0.0,30.0); fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10.0, 15.0, 20.0))); fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20.0, 25.0, 30.0))); fsTips.Output().Add(fvTips);
- Will create fuzzy rules, which altogether will present the knowledge base for our system. To create a rule, it is required to call a method ParseRule from the object, which presents our system, and as an option to give it a simple string representation of fuzzy rules:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)"); MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)"); MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");
Writing fuzzy rules is strictly typed and does not allow the use of non-key words. The keywords are: "if", "then", "is", "and", "or", "not", "(", ")", "slightly", "somewhat", "very", "extremely ". The last four keywords are the linguistic quantifiers. Also, all variable names, terms and functions available on your system are included in the list of keywords. The importance of fuzzy terms or Sugeno linear functions is increased or, conversely, reduced with the linguistic quantifiers. The following implementation of the linguistic quantifiers applies:
- "slightly" — replaces the condition result with its cube root. Greatly reduces value.
- "somewhat" — replaces the condition result with its square root. Reduces value.
- "very" — brings the condition result to the second level. Increases value.
- "extremely" — brings the condition result to the third level. Greatly increases value.
- "slightly" — replaces the condition result with its cube root. Greatly reduces value.
- The remaining step is to add rules to the system:
fsTips.Rules().Add(rule1); fsTips.Rules().Add(rule2); fsTips.Rules().Add(rule3);
Now we have a ready-made model for calculating tips based on the system of Mamdani fuzzy inference.
2.2. Designing Sugeno-type Systems
As an example of the implementation of Sugeno-type system, we will use a script for measuring the necessary control of a cruise control system in a car. This script is described in the file Cruise_Control_Sample_Sugeno.mq5 in the FuzzyNet Library for MQL5 and serves as one of the examples of fuzzy models application for solving problems of automatic control.
Fuzzy logic is mostly used for equivalent one-dimensional tasks in automatic control systems (ACS). Setting these goals can be described as following: an object at a certain point in time ![]() is in a state "A", and during time frame
is in a state "A", and during time frame ![]() it has to reach a condition "B". To solve similar tasks, the overall time frame is split into
it has to reach a condition "B". To solve similar tasks, the overall time frame is split into ![]() parts, a time step equal to
parts, a time step equal to ![]() is located, and then automatic control system manages it at every point
is located, and then automatic control system manages it at every point ![]() , where i = 0,1,2 ... n.
, where i = 0,1,2 ... n.
Various PID controllers can easily handle this task, but they have one drawback, as they are unable to work out a "smooth" control. In other words, if you build a cruise control system of a car based on the PID controller, with a change of speed the system will adjust to the desired speed, however, jumps and jolts may occur in the process. From a human's perspective, the fuzzy controller can perform smoother and with more comfort.
It becomes obvious that on the output of our fuzzy controller there will be a required velocity change of acceleration, and on the input an error and a first error derivative will occur. Error is a current state deviation from the desired one. In other words, the system input will be receiving the following information:
- the difference between the speed of the vehicle at the current moment and the speed set in the cruise control system;
- how quickly this difference decreases (increases).
So, the first input parameter of the "speed error" will range from -20 to 20 km/h and have three terms "slower", "zero", "faster". All three terms will have a triangular membership function. The second input — "SpeedErrorDot" ranges from -5 to 5, and operates fuzzy terms "slower", "zero", "faster" also with a triangular membership function.
Since our model has Sugeno inference system, the output value of "accelerate" will not have a maximum and minimum value, and instead of fuzzy terms there will be linear combinations of the input variables, which will also have names: "zero", "faster", "slower", "func". Let's describe all four linear combinations. For this we denote variables SpeedError as ![]() , SpeedErrorDot as
, SpeedErrorDot as ![]() , and Accelerate as
, and Accelerate as ![]() to obtain the following equations:
to obtain the following equations:
- zero:
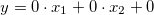 ;
; - faster:
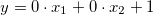 ;
; - slower:
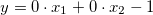 ;
; - func:
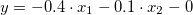 .
.
The knowledge base of this system will consist of nine rules:
- If the (speed error is slower), and (the speed error dot is slower), the acceleration is faster.
- If the (speed error is slower), and (the speed error dot is zero), the acceleration is faster.
- If the (speed error is slower), and (the speed error dot is faster), the acceleration is zero.
- If the (speed error is zero), and (the speed error dot is slower), the acceleration is faster.
- If the (speed error is zero), and (the speed error dot is zero), the acceleration is func.
- If the (speed error is zero), and (the speed error dot is faster), the acceleration is slower.
- If the (speed error is faster), and (the speed error dot is slower), the acceleration is faster.
- If the (speed error is faster), and (the speed error dot is zero), the acceleration is slower.
- If the (speed error is faster), and (the speed error dot is higher), the acceleration is slower.
Let's describe the course of the system creation:
- We include the file SugenoFuzzySystem.mqh from the FuzzyNet library for MQL5:
#include <Math\FuzzyNet\SugenoFuzzySystem.mqh>This file allows you to create Sugeno type systems and work with them. - Now we can create an empty Sugeno system and proceed with filling it in:
SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem(); - Input variables for Sugeno system are created the same way as for the Mandani-type system.
We will create the variable "SpeedError" and add it to the system:
FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0); fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0))); fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0))); fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));
We will create the variable "SpeedErrorDot" and also add it to the system:
FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
- We will create the Sugeno-type fuzzy variable which will be the output of the system. When creating a fuzzy variable a constructor accepts its name as the only parameter. Linear functions can be added to it, but first, these functions need to be determined, and for this we need an array of coefficients type double.
Formation of a linear function is conducted the following way: each input variable will be an unknown quantity of an equation with coefficients obtained from an array of coefficients. This way, coefficients in an array must be placed in the same order in which the input variables were recorded. Thus, for first input variable a coefficient of index 0 will apply, for second — index 1 etc. Therefore, length of an array of coefficients must be greater than a unit or a number equal to input variables. If lengths are equal, then a coefficient of a free term equals zero, otherwise its value will be equal to the last element of an array.
The are two input variables in our system, so the length of the arrays of coefficients should not exceed three. We will declare all four arrays, based on their information we will form the functions described above and add them to a Sugeno-type fuzzy variable and then include them in the system:SugenoVariable *svAccelerate=new SugenoVariable("Accelerate"); double coeff1[3]={0.0,0.0,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1)); double coeff2[3]={0.0,0.0,1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2)); double coeff3[3]={0.0,0.0,-1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3)); double coeff4[3]={-0.04,-0.1,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4)); fsCruiseControl.Output().Add(svAccelerate);
- Respectively with the Mamdani system we will create nine fuzzy rules:
SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)"); SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)"); SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)"); SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)"); SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)"); SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
- We will add them to our system:
fsCruiseControl.Rules().Add(rule1); fsCruiseControl.Rules().Add(rule2); fsCruiseControl.Rules().Add(rule3); fsCruiseControl.Rules().Add(rule4); fsCruiseControl.Rules().Add(rule5); fsCruiseControl.Rules().Add(rule6); fsCruiseControl.Rules().Add(rule7); fsCruiseControl.Rules().Add(rule8); fsCruiseControl.Rules().Add(rule9);
2.3. Calculation of Mamdani-type and Sugeno-type systems
A fuzzy variable and its value should be sent to the input of a fuzzy system. As mentioned above, fuzzy variables take value from their term sets. Therefore, the calculation result of the system will depend on the membership functions which correspond to the terms applied at the input with fuzzy input variables. However, in most cases, fuzzy variables are sent to the input system in form of simple numerical values, which are aimed to get accurate same form results on the output. In this case it turns out that the fuzzy term has no apparent declaration and its membership function is represented as a constant membership function. The systems written using FuzzyNet library are designed to operate with such a particular case.
What exactly needs to be sent to the input of the system and in what form will we get the results from it?
The number of input variables for fuzzy systems is not limited, each entry must take some values, therefore, we need to have a list which will store values for each input. A complex object with two fields should be the element of this list: first field — fuzzy variable, second field — numeric value type double. In the file Dictionary.mqh, taken from the library FuzzyNet in MQL5, the class Dictionary_Obj_Double is implemented allowing to create such objects.
We will form an input list for our Mamdani-type system:
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
Here Service and Food - are two input parameters of type double.
In the examples described above, both Mamdani and Sugeno systems have only one output, although in general, the same as with inputs, there are no restrictions for their amount. The structure of input and output does not have any differences.
The output for Mamdani-type systems:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
Now, for each system we will call a function Calculate which takes one parameter — a list of inputs, and returns a list of outputs. According to index 0 from the list, we will get the system output value, which is represented as an object of class Dictionary_Obj_Double. Using for this object methods Key and Value we can get a variable and, respectively, its result.
We will make a calculation for a Mamdani-system and display the received number in a fuzzy output variable fvTips:
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("Tips, %: ",p_od_Tips.Value());
We shall do the same with the Sugeno-type system:
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);
Conclusion
For more information about the scripts described above, as well as to create your fuzzy model, please download the FuzzyNet library for MQL5 or MQL4. It is essential to understand that the construction of "live" fuzzy models is a challenging job even with the assistance of auxiliary libraries. Furthermore, each finished model requires thorough mandatory checks and adjustments.
List of References and Links
- http://www.bindichen.co.uk/post/AI/mamdani-fuzzy-model.html — Mamdani fuzzy model.
- http://www.bindichen.co.uk/post/AI/takagi-sugeno-fuzzy-model.html — Sugeno fuzzy model.
- http://reference.wolfram.com/applications/fuzzylogic/DemonstrationNotebooks/5.html — fuzzy logic control.
- http://plato.stanford.edu/entries/logic-fuzzy — Fuzzy Logic Introduction.
- Lotfi A. Zadeh. Fuzzy sets and their applications
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/1991
 How to Develop a Profitable Trading Strategy
How to Develop a Profitable Trading Strategy
 Price Action. Automating the Engulfing Pattern Trading Strategy
Price Action. Automating the Engulfing Pattern Trading Strategy
 Price Action. Automating the Inside Bar Trading Strategy
Price Action. Automating the Inside Bar Trading Strategy
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
hi
when i updated metatrader to build 2342
all of samples with fuzzy logic library
return error "incorrect casting of pointers" on MQL5\Include\Math\Fuzzy\RuleParser.mqh Line 712
please help to fix bug
many thanks
read my previous post.
hi
thanks for your replay
real author is Dmitry Kalyuzhny. but his coded this library in .Net
But maybe someone else changed the code to mql
i see the author of this article is Дмитрий Калюжный
but I could not find Дмитрий Калюжный profile on mql5
Would you please help me to contact or fix this bug
many thanks
New article An Introduction to Fuzzy Logic has been published:
Author: MetaQuotes Software Corp.
Hi
when i updated metatrader to build 2342
all of samples with fuzzy logic library
return error "incorrect casting of pointers" on MQL5\Include\Math\Fuzzy\RuleParser.mqh Line 712
please help to fix bug
many thanks
hi
thanks for your replay
real author is Dmitry Kalyuzhny. but his coded this library in .Net
But maybe someone else changed the code to mql
i see the author of this article is Дмитрий Калюжный
but I could not find Дмитрий Калюжный profile on mql5
Would you please help me to contact or fix this bug
many thanks
If no one helps on this thread so you can use Freelance for example.
Hi guys,
I have a question regarding the 'linguistic Quantifiers': "slightly", "somewhat", "very", "extremely "...
What is the correct use of them in the ParseRule-function?
If I try something like this:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is very cheap)");...I get this error: "Conclusion part of the rule should be in form: 'variable is term'"
Where would I have to place the 'very' in the string above?
Help would be much apreciated!
Thanks!