交易中的机器学习:理论、模型、实践和算法交易 - 页 436 1...429430431432433434435436437438439440441442443...3399 新评论 [删除] 2017.06.30 17:46 #4351 elibrarius。 它正在工作,谢谢你有趣的是它是如何工作的... 它是寻找1个最相似的选项,还是对几个选项进行平均?显然,它能找到1个最好的。我想我应该去找10个甚至100个变体,并寻找平均预测值(具体数字应该由优化器决定)。 是的,这里显示了1个最好的,没有理会许多变体,如果你理解我的写作,你可以尝试重做 ) Женя 2017.06.30 21:20 #4352 交易员博士。我一直没能学会如何仅用价格进行盈利交易。但模式模型做到了,所以选择很明显 :)找到一个 "模式 "是一回事,但它带来的统计优势是另一回事。IMHO我非常怀疑,因为某些原因。事实上,通过沿历史序列的整个长度进行卷积(乘积、差值)与平均化来寻找模式,就像在NS中用一个神经元做回归,那是最简单的线性模型,具有极其愚蠢的标志,是价格的一个片断,因为它是。 Aleksei Kuznetsov 2017.06.30 21:39 #4353 吉安尼。找到一个 "模式 "是一回事,但找到一个统计上的优势又是另一回事。IMHO,我非常怀疑。事实上,在整个历史序列的长度上通过卷积(乘积、差值)寻找模式,这就像在NS中用一个神经元做回归,这是最简单的线性模型,具有极其愚蠢的特征,是价格的一个片断,因为它是。如果它是一个单一的神经元,那么输入的数量等于图案的长度,(图案为30条=30个NSb输入,500条=500个NS输入)。在我看来,NS内部层的许多神经元类似于存储器,10 - 50 - 100个额外的神经元相应地是10 - 50 - 100个输入信号的记忆变体。将这个模式与历史上的375000个变体(一年的M1)相比较,我们有一个绝对准确和完整的记忆,而不是10-50-100个最经常遇到的变体。然后,从这个记忆中,模式发现者识别出N个最相似的结果,并得到平均预测,而神经网络则增加每个相似模式的神经元之间的连接权重。 也不清楚为什么要应用卷积,我假设你建议将所寻找的模式与历史上的每个变体进行卷积,结果是我们得到了第三个时间序列--它如何帮助确定模式和被检查的变体的相似性? Женя 2017.06.30 22:58 #4354 elibrarius。如果是一个神经元,那么与输入的数量等于模板的长度,(模板的30条=30个NS输入的500条=500个NS输入)。 正是如此。elibrarius: 另一个不清楚的地方是为什么要应用卷积,我假设你建议将搜索到的模式与历史上的每个变体进行卷积,结果我们得到第三个时间序列--以及它如何帮助定义模式和测试变体的相似性? 你尽量减少模式和极值最相似的系列,就这么简单。例如,你有一个范围{0,0,0,1,2,3,1,1},你想在其中找到一个图案{1,2,3}。 通过折叠,你可以得到{0,0,0,3,8,14,11,8,6}(用眼睛计算)14个最多我们图案的 "头 "在哪。当然,在卷积之前最好对向量进行归一化处理(mo=0,length=1),否则在数字大的地方会有极值。 Aleksei Kuznetsov 2017.06.30 22:59 #4355 马克西姆-德米特里耶夫斯基。 是的,它在这里显示了1个最好的,没有理会许多变体,如果你理解我的写作,你可以试着重做它 )在看照片的时候,有些地方不太对劲... 这里有一个随机的例子你的蓝色预测线非常陡峭地向下,有一个类似变体的薄弱运动... 这里只是照了这个变体,看起来没有那么陡峭,按想法来说更合理。 [删除] 2017.06.30 23:06 #4356 elibrarius。当我在看照片的时候,有些地方不太对劲...... 这里有一个随机的例子你的蓝色预测线非常陡峭地下降,有一个类似的变体的微弱运动... 这里只是照了这个变体,结果不是那么陡峭,按想法更合理。注意到了:)在某些情况下,由于某种原因,它不能正确计算角度,这是从我把它从单时间框架版本改写成多时间框架版本开始的,我仍然没有弄清楚缺陷在哪里。顺便说一句,有可能是我根本没有算对......我没有想到用Photoshop检查。前面的图表和预测之间的角度应该是一样的 Aleksei Kuznetsov 2017.06.30 23:06 #4357 吉安尼。 正是如此。 你把模式和极端情况最相似的那一行折叠起来,这很简单。例如,你有一行{0,0,0,1,2,3,1,1},你想在其中找到一个图案{1,2,3},卷积会给你{0,0,0,3,8,14,11,8,6}(用眼睛计算)14最多我们图案的 "头部 "在哪里。当然,在卷积之前最好对向量进行归一化处理,否则在数字大的地方会出现极值。为什么要把事情搞得这么复杂?如果我们可以在{0,0,0,1,2,3,1,1,1}行中具体寻找{1,2,3},我们为什么要在卷积上寻找极值?除了增加复杂性和计算时间外,我没有看到任何好处。 Женя 2017.06.30 23:08 #4358 elibrarius。为什么要把事情搞得那么复杂?如果我们可以在{1,2,3}系列中具体寻找{0,0,0,1,2,3,1,1},我们为什么要在卷积上寻找极值?除了复杂化和更长的计算时间之外,我看不出有什么好处。嗯......你说的 "专门搜索 "是什么意思?请给我一个比卷积法更快的算法的例子。可以使用两种操作:向量差长和标量积,差长,相信我是3-10倍的速度,分量差,平方,和,根提取,卷积就是乘法和加法。你需要把每一块长度为3的行作为一个向量,并将其与我们的{1,2,3}进行 "相似性 "比较。 Aleksei Kuznetsov 2017.06.30 23:21 #4359 吉安尼。嗯......你说的 "专门搜索 "是什么意思?请给我一个比卷积更快的算法的例子。最简单的方法是在整个序列中逐步移动所寻找的例子的窗口宽度,并找到deltas的abs.值的总和。 0,0,0和1,2,3的误差=(1-0)+(2-0)+(3-0)=60,0,1和1,2,3的误差=(1-0)+(2-0)+(3-1)=50,1,2和1,2,3的误差=(1-0)+(2-1)+(3-2)=31,2,3和1,2,3误差=(1-1)+(2-2)+(3-3)=02,3,1和1,2,3误差=(2-1)+(3-2)+Abs(1-3)=4其中最小的误差是最大的相似度。 Aleksei Kuznetsov 2017.06.30 23:35 #4360 马克西姆-德米特里耶夫斯基。注意到:)在某些情况下,由于某些原因,它不能正确计算角度,这是在我从单时间框架版本改写为多时间框架版本后开始的,而且从未发现错误所在。顺便说一下,有可能我根本就算错了......我没有设法用Photoshop检查。我应该在以前的图表和预测之间得到相同的角度。我还不确定,在斜率角相差如此之大的情况下,将图形视为相似是正确的。用同样的例子。发现的变体给出了从上行趋势点或趋势结束时的回撤,通过将其转移到形态图上,它将给出下降趋势的继续而不是逆转的预测--本质上是一个反向信号。这里有些不对劲....也许我们不需要这些仿生变换....?而简单的相关关系(最小的误差)就足够了? 1...429430431432433434435436437438439440441442443...3399 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
它正在工作,谢谢你有趣的是它是如何工作的...
它是寻找1个最相似的选项,还是对几个选项进行平均?显然,它能找到1个最好的。我想我应该去找10个甚至100个变体,并寻找平均预测值(具体数字应该由优化器决定)。
是的,这里显示了1个最好的,没有理会许多变体,如果你理解我的写作,你可以尝试重做 )
我一直没能学会如何仅用价格进行盈利交易。但模式模型做到了,所以选择很明显 :)
找到一个 "模式 "是一回事,但它带来的统计优势是另一回事。IMHO我非常怀疑,因为某些原因。事实上,通过沿历史序列的整个长度进行卷积(乘积、差值)与平均化来寻找模式,就像在NS中用一个神经元做回归,那是最简单的线性模型,具有极其愚蠢的标志,是价格的一个片断,因为它是。
找到一个 "模式 "是一回事,但找到一个统计上的优势又是另一回事。IMHO,我非常怀疑。事实上,在整个历史序列的长度上通过卷积(乘积、差值)寻找模式,这就像在NS中用一个神经元做回归,这是最简单的线性模型,具有极其愚蠢的特征,是价格的一个片断,因为它是。
如果它是一个单一的神经元,那么输入的数量等于图案的长度,(图案为30条=30个NSb输入,500条=500个NS输入)。
在我看来,NS内部层的许多神经元类似于存储器,10 - 50 - 100个额外的神经元相应地是10 - 50 - 100个输入信号的记忆变体。将这个模式与历史上的375000个变体(一年的M1)相比较,我们有一个绝对准确和完整的记忆,而不是10-50-100个最经常遇到的变体。然后,从这个记忆中,模式发现者识别出N个最相似的结果,并得到平均预测,而神经网络则增加每个相似模式的神经元之间的连接权重。
也不清楚为什么要应用卷积,我假设你建议将所寻找的模式与历史上的每个变体进行卷积,结果是我们得到了第三个时间序列--它如何帮助确定模式和被检查的变体的相似性?如果是一个神经元,那么与输入的数量等于模板的长度,(模板的30条=30个NS输入的500条=500个NS输入)。
另一个不清楚的地方是为什么要应用卷积,我假设你建议将搜索到的模式与历史上的每个变体进行卷积,结果我们得到第三个时间序列--以及它如何帮助定义模式和测试变体的相似性?
是的,它在这里显示了1个最好的,没有理会许多变体,如果你理解我的写作,你可以试着重做它 )
在看照片的时候,有些地方不太对劲...
这里有一个随机的例子
你的蓝色预测线非常陡峭地向下,有一个类似变体的薄弱运动...
这里只是照了这个变体,看起来没有那么陡峭,按想法来说更合理。
当我在看照片的时候,有些地方不太对劲......
这里有一个随机的例子
你的蓝色预测线非常陡峭地下降,有一个类似的变体的微弱运动...
这里只是照了这个变体,结果不是那么陡峭,按想法更合理。
注意到了:)在某些情况下,由于某种原因,它不能正确计算角度,这是从我把它从单时间框架版本改写成多时间框架版本开始的,我仍然没有弄清楚缺陷在哪里。
顺便说一句,有可能是我根本没有算对......我没有想到用Photoshop检查。前面的图表和预测之间的角度应该是一样的
正是如此。
你把模式和极端情况最相似的那一行折叠起来,这很简单。例如,你有一行{0,0,0,1,2,3,1,1},你想在其中找到一个图案{1,2,3},卷积会给你{0,0,0,3,8,14,11,8,6}(用眼睛计算)14最多我们图案的 "头部 "在哪里。当然,在卷积之前最好对向量进行归一化处理,否则在数字大的地方会出现极值。
为什么要把事情搞得这么复杂?如果我们可以在{0,0,0,1,2,3,1,1,1}行中具体寻找{1,2,3},我们为什么要在卷积上寻找极值?除了增加复杂性和计算时间外,我没有看到任何好处。
为什么要把事情搞得那么复杂?如果我们可以在{1,2,3}系列中具体寻找{0,0,0,1,2,3,1,1},我们为什么要在卷积上寻找极值?除了复杂化和更长的计算时间之外,我看不出有什么好处。
嗯......你说的 "专门搜索 "是什么意思?请给我一个比卷积法更快的算法的例子。
可以使用两种操作:向量差长和标量积,差长,相信我是3-10倍的速度,分量差,平方,和,根提取,卷积就是乘法和加法。
你需要把每一块长度为3的行作为一个向量,并将其与我们的{1,2,3}进行 "相似性 "比较。
嗯......你说的 "专门搜索 "是什么意思?请给我一个比卷积更快的算法的例子。
最简单的方法是在整个序列中逐步移动所寻找的例子的窗口宽度,并找到deltas的abs.值的总和。
0,0,0和1,2,3的误差=(1-0)+(2-0)+(3-0)=6
0,0,1和1,2,3的误差=(1-0)+(2-0)+(3-1)=5
0,1,2和1,2,3的误差=(1-0)+(2-1)+(3-2)=3
1,2,3和1,2,3误差=(1-1)+(2-2)+(3-3)=0
2,3,1和1,2,3误差=(2-1)+(3-2)+Abs(1-3)=4
其中最小的误差是最大的相似度。
注意到:)在某些情况下,由于某些原因,它不能正确计算角度,这是在我从单时间框架版本改写为多时间框架版本后开始的,而且从未发现错误所在。
顺便说一下,有可能我根本就算错了......我没有设法用Photoshop检查。我应该在以前的图表和预测之间得到相同的角度。
我还不确定,在斜率角相差如此之大的情况下,将图形视为相似是正确的。用同样的例子。
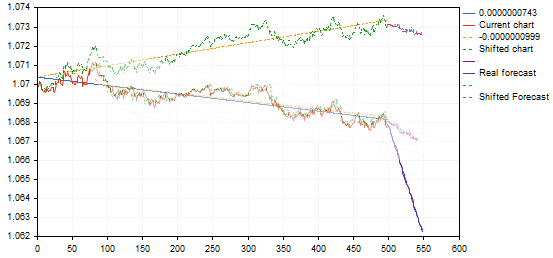
发现的变体给出了从上行趋势点或趋势结束时的回撤,通过将其转移到形态图上,它将给出下降趋势的继续而不是逆转的预测--本质上是一个反向信号。这里有些不对劲....也许我们不需要这些仿生变换....?而简单的相关关系(最小的误差)就足够了?