kiracı - sayfa 16
Ticaret fırsatlarını kaçırıyorsunuz:
- Ücretsiz ticaret uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
Bu parametrelerin sonucu nasıl etkilediğini görmek ilginçtir:
Örneğin, başlangıç koşullarımız için çeşitli valf konumlarında böyle ilginç resimler elde ederiz.
.
.
.
Peki, bu büyük resim için...
Burada son bağımlılıkla ilgileniyoruz
(faz portresi "a - da" - son grafik - özel durumu)
Ondan iyi bir şey çıkmadı. Hesapları buraya yazmayacağım. Onlar hakkında güzel bir şey yok.
Şu gözlemi kullanmaya çalıştım: 1+qk = 1+epsilon ve epsilon küçük bir değer. Daha sonra, terimleri üçüncü küçüklük mertebesine kadar tutarak, bir Taylor serisinde k'ye göre türevi genişletti. Daha sonra sadeleştirmelerden sonra kübik bir denklem elde edilmiştir. İçinde epsilon'da üçüncü dereceden küçüklük terimini çıkardım ve elde edilen kareyi çözmeye çalıştım. Başarısız: diskriminant yalnızca küçük t için pozitiftir.
Korkarım ki kübik terimi atarak bir hata yaptım: epsilon'daki üçüncü küçüklük düzeninin bir üyesi olmasına rağmen, küçük değil. Bunu şöyle yaptım: epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3). Genel olarak t oldukça büyük olabileceği görülebilir (epsilon~0.01 oldukça gerçekçi bir varsayım olsa bile). Ve kübik olanı çözmek istemiyorum.
Bakalım Oleg'e ne olacak.
PS epsilon*t = O (1) (veya q*t = O (1) ) varsayıldığında, bir güç fonksiyonu üstel olarak tahmin edilebilir. Hadi deneyelim...
Başka bir yaklaşım daha var - Taylor serisi olmadan, ancak basitçe tanjant yöntemiyle (görünüşe göre Newton). Ayrıca oldukça doğru bir analitik çözüme de ulaşabilirsiniz.
Gerçek şu ki, başlangıçta, koşullarda sürekli zaman değil, bir kafes işlevi - yani. önce uygun dönüşümü yapmanız gerekir. Ancak o zaman küçük bir epsilonun tanıtımı meşru olacaktır. Bunlar kafes fonksiyonlarının özellikleridir.
Bu arada, problemi çözmenin ilk adımında, ayrık-frekans--zaman zincirinde Laplace dönüşümünü kullanarak meşgul olduğum sürekli zaman bölgesine çevirme oldu. Veya daha doğrusu: dahil ve bu ...
Dolayısıyla, ileri analizimizin amacı fonksiyondur.
.
Ve kübik olanı çözmek istemiyorum.
Alexey , kübik bir denklemin kökleri için hiç analitik bir ifade görmedim (belirli basitleştirilmiş durumlar hariç). sende öyle biri yok mu İkinci dereceden bir denklem için nasıl olurdu: x1=b/2+SQRT()... vb. Biliyorsanız yayınlayın. İnternette hiçbir şey bulamadım. Harmonik fonksiyonlar aracılığıyla köklerin bir temsilinin bile olduğunu okuldan hatırlıyorum!
Başka bir yaklaşım daha var - Taylor serisi olmadan, ancak basitçe tanjant yöntemiyle (görünüşe göre Newton). Ayrıca oldukça doğru bir analitik çözüme de ulaşabilirsiniz.
Bu şekilde analitik biçimde yaklaşık bir çözüm elde etmek gerçekten mümkün mü? Hiç duymadım. Çok ilginç, yöntemin uygulamasını bir örnekte görmek isterim.
Stüdyoya!
Evet, büyük t için ortaya çıkan çözümden bahsediyorsunuz. Bu, aynı zamanda, "yok edilemez" bir mevduat durumunda olduğu gibi, pratik açıdan da ilgi çekicidir. Ne için bir yaklaşım elde etmeyi başardınız ? Belki de t->inf için bir limit geçişi mümkündür ... Ardından, çekilen fonların optimal yüzdesi - k , sadece bir parametre q - tahakkuk eden faiz tutarının bir fonksiyonu olarak analitik bir ifade elde edeceğiz. Bu harika bir sonuç olurdu.
otomatik :
Gerçek şu ki, başlangıçta, koşullarda sürekli zaman değil, bir kafes işlevi - yani. önce uygun dönüşümü yapmanız gerekir. Ancak o zaman küçük bir epsilonun tanıtımı meşru olacaktır. Bunlar kafes fonksiyonlarının özellikleridir.
Bu arada, problemi çözmenin ilk adımında, ayrık-frekans--zaman zincirinde Laplace dönüşümünü kullanarak meşgul olduğum sürekli zaman bölgesine çevirme oldu. Veya daha doğrusu: dahil ve bu ...
Oleg , neden çekilen fonların toplamı için yukarıdaki analitik ifadenin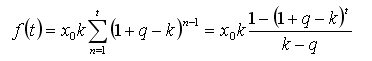
sürekli zaman için sınırlayıcı değil mi? Ne de olsa, orijinal zaman serisinin (konunun ilk gönderisinde yinelemeli bir kayıt şekli) minimum aralığı (adım) üzerinde özel olarak bir kısıtlama getirmedik. Eğer öyleyse, dt->0 olarak limite geçerken belirli bir df(t)' ye sahip olmamız ve hiçbir çelişki olmaması yeterlidir...
Oleg , çekilen fonların toplamı için yukarıda elde edilen analitik ifadenin neden sürekli zaman için sınırlı olmadığını düşünüyorsunuz? Ne de olsa, orijinal zaman serisinin (konunun ilk gönderisinde yinelemeli bir kayıt şekli) minimum aralığı (adım) üzerinde özel olarak bir kısıtlama getirmedik. Eğer öyleyse, dt->0 olarak limite geçerken belirli bir df(t)' ye sahip olmamız ve hiçbir çelişki olmaması yeterlidir...
yanlış... Buraya küçük bir epsilon girmeye çalışın...
Evet, herhangi bir yeri özel olarak şart koşmadık, ancak sorunun formülasyonu, örtük olarak bir kafes fonksiyonunun kullanımını ima ediyor.
Bu, eşleşmenin kafes düğümlerinde olacağı anlamına gelir. Ayrıca, kafes fonksiyonları için ara noktalar yoktur - sadece kafes düğümleri. Bu nedenle, ara değerler oluşturma girişimleri hatalı sonuçlara yol açar (bu arada, bu sorular sinyal niceleme alanındandır). Ara değerler oluşturmak için örnekleme oranını artırabilirsiniz, yani. fenomenin özünü temelden değiştirmeyecek daha fazla sayıda düğüme sahip bir kafes fonksiyonunu tekrar tanıtın. Bu, özellikle, birinci, ikinci vb. türevleri, birinci, ikinci vb. kullanılır. farklılıklar. İntegral yerine toplamlar. ... vb. bütün bir araştırma alanıdır.
Ancak bir bölgeden diğerine geçmenin ve geri dönmenin yolları var.
Bize verilen belirli bir durumda bir görevin kararının görünümü - böyle bir yaklaşım uygun değildir. Bu nedenle, yapmamız gereken ilk şey kesikli zamandan sürekli zamana geçmektir.
Gerçek şu ki, başlangıçta, koşullarda sürekli zaman değil, bir kafes işlevi - yani. önce uygun dönüşümü yapmanız gerekir.
Kübik bir denklemin kökleri için hiç analitik bir ifade görmedim (belirli basitleştirilmiş durumlar hariç). Sende öyle biri yok mu İkinci dereceden bir denklem için nasıl olurdu: x1=b/2+SQRT()... vb. Biliyorsanız yayınlayın. İnternette hiçbir şey bulamadım.
formül Cardano
Harmonik fonksiyonlar aracılığıyla köklerin bir temsilinin bile olduğunu okuldan hatırlıyorum!
Vieta'nın trigonometrik formülü
... veya üretmemek, ancak Laplace dönüşümünün ayrık versiyonunun mevcut aparatını kullanmak, yani. Z-dönüşümleri. Daha kolay olacağını düşünmüyor musun?
evet, bu gerçekten bir sorun değil. En başta üç boyutlu bir resim var "% büyüme -% kaldırma - karlılık" - her şey zaten hesaplandı ve ayrık bölgede.
Şimdi sportif görev, hepsini analitik bir biçimde sunmaktır;)
formül Cardano
Vieta'nın trigonometrik formülü