Есть метод, который значительно быстрее считает значение конца линейной регрессии
возможно ли используя данный метод получить наклон? Ну или значение на бар назад, самой линии регрессии, повторюсь, не LRMA.
Где подсмотрели этот метод?
https://www.mql5.com/ru/code/8200
Да. Одна из версий. В поиске смотрите LRMA.
Прилагаю картинку для наглядности.

- голосов: 8
- 2008.06.17
- Victor Nikolaev
- www.mql5.com
Нужен наклон линейной регрессии, то есть b из формулы "a+b*x". Но сама регрессия, если считать по классике занимает прилично ресурсов.
Есть метод, который значительно быстрее считает значение конца линейной регрессии
возможно ли используя данный метод получить наклон? Ну или значение на бар назад, самой линии регрессии, повторюсь, не LRMA.
Убрал код мкл4, просьба вернуть в раздел "Технические индикаторы и анализ рынка Форекс".
То есть пройтись циклом по барам, составляющим линейную регрессию, это затратно, а вот посчитать две средние на этих же барах - не затратно?
То есть пройтись циклом по барам, составляющим линейную регрессию, это затратно, а вот посчитать две средние на этих же барах - не затратно?
Ну и чем эта LRMA похожа на регрессию? Кстати, расчет регрессии довольно простой
Не согласен. Вызвать стандартные SMA и LWMA из стандартной поставки быстрее, чем рассчитать значение по a+b*x. Там же цикл на каждом баре суммирующий четыре значения, а это заметно снижает скорость. Проверял в тестере LRMA рассчитанной по классике и с помощью "3.0*LWMA-2.0*SMA", так со вторым вариантом гораздо быстрее получается.
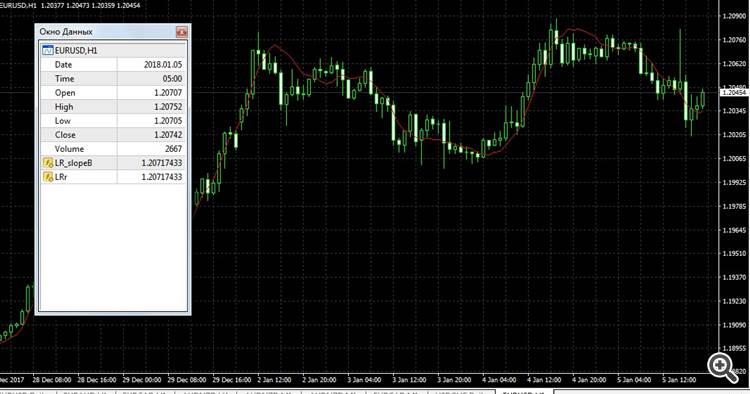
На картинке периоды индикаторов одинаковые и конечные значения на нулевом баре идентичны.
Не согласен. Вызвать стандартные SMA и LWMA из стандартной поставки быстрее, чем рассчитать значение по a+b*x. Там же цикл на каждом баре суммирующий четыре значения, а это заметно снижает скорость. Проверял в тестере LRMA рассчитанной по классике и с помощью "3.0*LWMA-2.0*SMA", так со вторым вариантом гораздо быстрее получается.
На картинке периоды индикаторов одинаковые и конечные значения на нулевом баре идентичны.
на самом деле просто близки в данном конкретном случае.
в линейную регрессию вообще довольно просто попасть :-) очень много чего к ней сходится по понятным причинам.
взвешенные по степеням МА-шки попадают точнее. Как-бы им положено из метода расчёта лин.регресии
и заменять расчёт лин.регресии на частные приближения смысла как-то невижу. К чему ? При желании она очень быстро считается..
на самом деле просто близки в данном конкретном случае.
в линейную регрессию вообще довольно просто попасть :-) очень много чего к ней сходится по понятным причинам.
взвешенные по степеням МА-шки попадают точнее. Как-бы им положено из метода расчёта лин.регресии
и заменять расчёт лин.регресии на частные приближения смысла как-то невижу. К чему ? При желании она очень быстро считается..
Ну, мне нужен наклон самой линии в углах. Давно задавался вопросом, если значение конца можно получить с помощью машки, то может как-то наклон можно получить.
Ладно, проехали. Уже все проверил)
Прилагаю картинку с двумя индикаторами один на классике сделан, другой по "быстрому" методу.
P.S. Который раз захожу спросить, а на самом деле сам больше рассказываю)
Нужен наклон линейной регрессии, то есть b из формулы "a+b*x". Но сама регрессия, если считать по классике занимает прилично ресурсов.
Что мудрить то? Выражение то простейшее.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
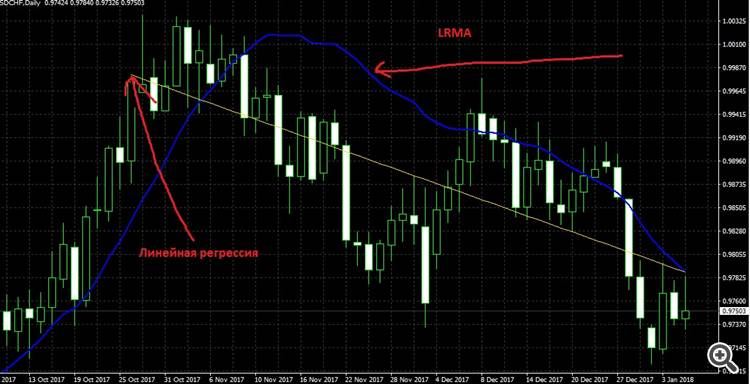
Нужен наклон линейной регрессии, то есть b из формулы "a+b*x". Но сама регрессия, если считать по классике занимает прилично ресурсов.
Есть метод, который значительно быстрее считает значение конца линейной регрессии
возможно ли используя данный метод получить наклон? Ну или значение на бар назад, самой линии регрессии, повторюсь, не LRMA.
Убрал код мкл4, просьба вернуть в раздел "Технические индикаторы и анализ рынка Форекс".