как немногие могут догадаться, эта короткая заметка - снова про старое и ранее на форуме упомянутое. В основном про корреляции
Сразу в лёт про то что не надо читать по утрам, то есть цитата (скриншот) википедии:
линейный коэф.корреляции или коэф. Пирсона:
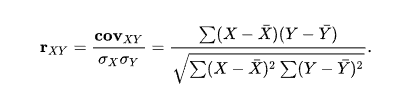
и далее:
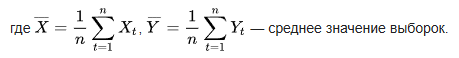
Так вот левая часть первой формулы верно и хрен поспоришь, а её правая часть читается чуть иначе чем привыкли
Второе, про среднеарифметическое - категорически неверно.
X,Y c чёрточками - центральная тенденция. Которая зависит от природы данных X,Y и желательно колмогоровское среднее (кстати, не обязательно).
Среднеарифметическое - это частный и довольно редкий случай.
X-X_c_чёрточкой - дистанция от отдельно взятой величины до центральной тенденции. "насколько конкретная точка далека от общей сэрэдыны"
Не обязательно минус, там может быть функция
Для того чтобы без страха применять википедную формулу (и функции/индикаторы MQL), исходные данные X,Y надо очень вдумчиво преобразовывать и приводить к виду:
- где X*Y имеет хоть какой-то смысл, (то есть ты можешь ответить на вопрос в чём измеряются и что обозначает сие произведение)
- средняя величина является центральной.
или выводить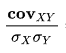 
для своего случая.
В чём подвох, с чего такие сложности ? Заговор педия-массонов, кругом обман, от нас что-то скрывают ??
всё проще - все формулы википедии скопипащены с источников, где чёрным по белому относятся к вероятностному пространству,
которое абстрактно и не вполне эквивалент физического. Зато оно обладает нужными требованиями.
И в уме держат отображения физического в вероятностное и обратно.
а у нас применяют прямо как есть прямо к любым данным напропалую, без тени сомнения..формула-же есть, чего её не применить-то :-) там ещё столько формул в мире - надо пробовать все пока грааль не вылезет
