Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
É óbvio que você deve se retirar q e somente no final do período t. Em todos os outros casos, a quantia retirada será inferior a
O ouriço-cacheiro decidiu utilizar cálculos analíticos))))
O problema não tem extremos, porque temos uma série numérica monotônica crescente - uma função com um argumento na forma do tamanho do depósito. Isto é, não há nada a ser otimizado. Quanto maior o argumento e t, maior o valor da função. Em qualquer outro caso, o valor da função irá diminuir.
É difícil procurar um gato preto em um quarto escuro, especialmente se ele não estiver lá (c) Confúcio
Tudo o que resta é tomar o tempo derivado e equacioná-lo a zero. Sim.
A propósito, se alguma coisa, a derivada deve ser assumida k
Perdão! Realmente na k .
Reshetov:
É óbvio que você tem que se retirar q e somente no final do período t. Em todos os outros casos, a quantia retirada será menor.
Yura, você está tão confiante de que é engraçado quando você está errado.
Na primeira página, avtomat deu uma imagem onde você pode ver claramente o ótimo sobre o parâmetro k . Talvez você simplesmente não tenha notado. Eu lhe mostrarei outro:
Você vê o máximo? Não? Mas ele está lá!
Descanse um pouco, seu ouriço-cacheiro.
De jeito nenhum!...
Você pode ser mais específico? Quer dizer, sob a forma de uma fórmula.
Em outras palavras, o ótimo em termos de porcentagem de retirada é de fato visível!
Recentemente resolvi um problema semelhante...
E então combinamos tudo isso e obtemos a função resultante de duas variáveis.
Também deve ser mencionado que o resultado depende do período de otimização, ou seja
o ótimo para 12 meses não é igual a quatro ótimos para períodos de 3 meses.
Recentemente resolvi um problema semelhante...
É isso mesmo, avtomat. É exatamente assim que ele se comporta. Mas eu realmente preciso obter uma solução analítica para a fração ideal de k. Se você pegar a derivada de k de f(k), você obtém a seguinte equação: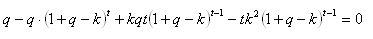
A figura abaixo mostra claramente que a abcissa onde df/dk é zero coincide com o máximo de f(k).
Mas como resolvê-lo com respeito à k?
Bem, o problema não tem nada a ver com o comércio de qualquer maneira. É um problema com o rentier. Seria bastante adequado para esse ramo.
P.S., o que será que o Jura fará nesta situação? Ele vai fingir que não notou nada (sem máximo no parâmetro k ) e não deixar comentários sobre o assunto ou terá que reconsiderar suas suposições básicas para a vida...
P.S. O que será que o Jura vai fazer nesta situação? Ele fingirá não notar nada (não há máximo para o parâmetro k ) e não deixará mais comentários sobre o assunto ou terá que reconsiderar seus principais pontos de ajuste para a vida...
Tenho permissão para usar um depósito de rublos X0 durante t meses. Todo mês o depósito é creditado com uma porcentagem fixa q do valor do depósito atual X. Estou autorizado a retirar mensalmente uma certa porcentagem k da conta que não exceda o valor de q.
Estou autorizado a abrir negócios com HO tamanho de lote. Cada comércio positivo aberto tem u% de chance de acumular pips, enquanto ganha q, é claro, do valor atual do depósito XO. Estou autorizado a fechar parcialmente um pedido por uma certa porcentagem k quantas vezes desejar (até 100% de fechamento) com uma freqüência de n pips que não exceda w.
Pergunta: Encontrar relativo a u%, valores ótimos de k, n.
É isso mesmo, avtomat. É exatamente assim que ele se comporta. Mas eu realmente preciso obter uma solução analítica para a fração ideal de remoção k. Se você pegar a derivada de k de f(k), você obtém a seguinte equação:
A figura abaixo mostra claramente que a abcissa onde df/dk é zero coincide com o máximo de f(k).
Mas como resolvê-lo com respeito à k?
se a equação acima for verdadeira, então podemos fazer isso:
Mas novamente, quais são os requisitos, quais são as condições...
q e t -- dadas quantidades constantes ou ...