Não consigo atravessar o labirinto de código, mas gostaria de compará-lo.
Cotação inicial
Temos as seguintes variantes de suavização:
Resultado da suavização
Equação de regressão:
eurusd = c(1)*eurusdsm(-1) + c(2)*tendência + c(3)
Estimativa da equação de regressão
| Variável | Coeficiente | Stand.osh. | Estatística t | probabilidade |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
R-quadrado = 0,788273
Erro padrão da regressão = 0,015172
Com base nos números obtidos, observamos que
todos os coeficientes de regressão são significativos (a probabilidade de sua igualdade a zero é igual a zero)
R-quadrado bastante alto (mas não muito alto), o que significa que a regressão explica 78% da variação
o erro padrão é de 151 pips. Esse é um número enorme.
Podemos confiar nos números resultantes?
Eu não confiaria, pois, de acordo com Jarque-Bera, a probabilidade de a série suavizada ter uma distribuição normal é de 31%.
Vamos fazer uma previsão:
O erro de previsão não fica muito atrás do erro de regressão e ultrapassa 100 pips
Vamos dar uma olhada no gráfico do erro de previsão:
Bem, este é um final completo: o erro é variável, o que significa que o comportamento futuro da previsão é desconhecido!
Para descobrir o motivo, vamos dar uma olhada na correlação dos coeficientes da equação de regressão:
Podemos considerar que os coeficientes c(1) e c(3) estão quase 100% correlacionados.
Minha conclusão é que não podemos usar a suavização exponencial para previsão.
Por que temos resultados diferentes?
É óbvio para mim que os parâmetros ideais que você encontrou não passam de um ajuste trivial. A regressão em si é inútil, seus coeficientes estão correlacionados.
É óbvio para mim que os parâmetros ideais que você encontrou não passam de um ajuste trivial. A regressão em si é inútil, pois os coeficientes nela contidos estão correlacionados.
Obrigado por seu interesse no artigo.
Por favor, esclareça o que você quis dizer. Quais resultados não convergem e quais são os parâmetros ideais?
Por favor, esclareça o que você quis dizer com isso.
Desculpe-me, você diz que pode usá-lo, mas minha conclusão é que não pode.
O que usar e por quê?
Em conclusão, deve-se observar que os modelos de suavização exponencial, em certos casos, são capazes de fornecer previsões tão precisas quanto as previsões obtidas com modelos mais complexos, confirmando mais uma vez o fato de que o modelo mais complexo nem sempre é o melhor.
Minha conclusão é que a suavização exponencial não deve ser usada para previsões.
Sobre o que são suas perguntas e por que você as faz?
Minha conclusão é que não é possível usar a suavização exponencial para fazer previsões.
Sobre o que são suas perguntas e para que elas servem?
Eu adoraria tentar responder algo, mas preciso saber a pergunta, pelo menos. Caso contrário, terei que adivinhar e fantasiar.
Vou tentar esclarecer novamente.
Os modelos de suavização exponencial não podem ser usados para prever o par eurusd, alguma citação ou nunca?
P.S..
Você tem em seu texto: "Equação de regressão:eurusd = c(1)*eurusdsm(-1) + c(2)*tendência + c(3)". Por que regressão, o artigo é sobre modelos de suavização exponencial, e há um modelo diferente, em vez de c(3) há uma variável aleatória com alguma distribuição e dispersão?
Em seu texto: "Equação de regressão:eurusd = c(1)*eurusdsm(-1) + c(2)*tendência + c(3)". Por que regressão, o artigo é sobre modelos de suavização exponencial, e há um modelo diferente, onde em vez de c(3) há uma variável aleatória com alguma distribuição e variância?
Isso não funciona, falar de cego para surdo. Vamos adiar isso.
Mais uma vez, parabéns pelo bom artigo.
Não está funcionando, falar de cego para surdo. Vamos adiar isso.
Mais uma vez, parabéns pelo bom artigo.
Na verdade, estou muito curioso para saber seu ponto de vista sobre a previsão usando a suavização exponencial. Há muitas coisas que eu simplesmente não sei e sempre fico feliz em tentar descobrir algo novo em todas as oportunidades, por isso estou fazendo perguntas.
Se não for muito difícil, explique por que, se a distribuição da sequência original (ou da sequência original suavizada) não for normal, a previsão não é confiável? Ou eu o entendi mal?
Obrigado pelos parabéns.
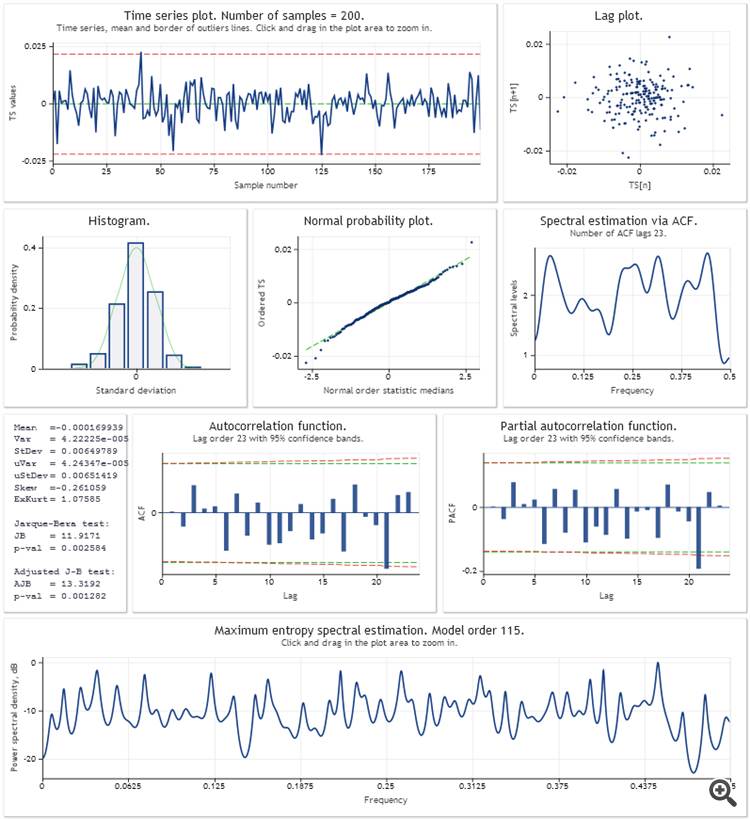
Aqui está uma análise de erro de previsão de um passo à frente para o modelo de crescimento linear aditivo com amortecimento. Os parâmetros do modelo foram otimizados usando uma amostra dos últimos 200 valores de USDJPY,M1. Da mesma forma que no script Optimisation_Test.mq5 do artigo.
https:// www.mql5.com/ru/articles/292
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Previsão de séries temporais utilizando suavização exponencial foi publicado:
O artigo familiariza o leitor com os modelos de suavização exponencial usados para previsão de curto prazo de séries de tempo. Além disso, ele toca em assuntos relacionados com a estimativa e otimização dos resultados de previsão e fornece alguns exemplos de scripts e indicadores. Este artigo será útil como primeira familiarização com os princípios de previsão baseados nos modelos de suavização exponencial.
Autor: Victor