Discussão do artigo "Distribuições estatísticas no MQL5 - tirando o melhor de R" - página 19

[Aleksey Nikolayev]

Aleksey Nikolayev:
Há um desejo de adicionar a distribuição de Kolmogorov à biblioteca. Ela é muito útil por causa de seu uso no critério de Kolmogorov-Smirnov e no problema de busca da decomposição de um processo aleatório.

Vou deixá-la aqui por precaução. Cálculo do CDF e suas adições para a distribuição da estatística de Kolmogorov-Smirnov para o teste de amostra única bilateral.

[Aleksey Nikolayev]

Alguém já usou isso?

[Renat Fatkhullin]

Aleksey Nikolayev:

O CDF da distribuição hipergeométrica é calculado incorretamente pela função MathCumulativeDistributionHypergeometric(). Por definição, a função de distribuição de probabilidade deve ser definida para qualquer número real. Abaixo está um script no mql5 com seus resultados e, para comparação, o mesmo no R.

resultado:

-1,0 nan 2

0.0 0.0 0

0,5 nan 2

divisão por zero em 'Hypergeometric.mqh' (241,35)

Resultado:

[1] 0.0000000 0.0000000 0.0000000 0.2222222

Você passou argumentos incorretos e obteve ERR_ARGUMENTS_INVALID (2). Estamos verificando os parâmetros de entrada com mais detalhes, e o R parece ter substituído a resposta por zeros.

//+------------------------------------------------------------------+
//| Função de distribuição cumulativa hipergeométrica (CDF)
//+------------------------------------------------------------------+
//| A função retorna a probabilidade de uma observação
//| da distribuição hipergeométrica com parâmetros m,n,k |
//| é menor ou igual a x.|
//||
//| Argumentos:|
//| x : O número desejado de objetos
//| m : Tamanho da população
//| k : Número de itens com a característica desejada
//|| na população|
//| n : Número de amostras retiradas
//| tail : Sinalizador para calcular a cauda inferior
//| log_mode : Modo de logaritmo, se verdadeiro, calcula os valores de log.
//| Error_code : Variável para o código de erro
//||
//| Valor de retorno:|
//| O valor da função de distribuição cumulativa hipergeométrica
//| com parâmetros m,n,k, avaliados em x. ||
//+------------------------------------------------------------------+
//| Baseado no algoritmo de John Burkardt|
//+------------------------------------------------------------------+
double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code)
  {
//--- verificar NaN
   if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- m,k,n,x deve ser um número inteiro
   if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x))
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- m,k,n,x devem ser positivos
   if(m<0 || k<0 || n<0 || x<0)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- intervalos de verificação
   if(n>m || k>m)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

[Renat Fatkhullin]

Aleksey Nikolayev:

Alguns (não todos) coeficientes binomiais são negativos, por exemplo:

resultado: -309196571788882235

deveria ser: 349615716557887488

Devido ao grande K (28), o long de 64 bits transbordou ali. O valor de retorno é longo.

Para contar valores dentro desses limites, você precisa reescrever a função para valores duplos.

[Aleksey Nikolayev]

Renat Fatkhullin:

Você passou argumentos incorretos e obteve ERR_ARGUMENTS_INVALID (2). Verificamos os parâmetros de entrada com mais detalhes, e o R parece ter substituído a resposta por zeros.

1) Qualquer CDF - função de distribuição de probabilidade (as discretas não são exceção!) DEVE DEFINITIVAMENTE ser definida para todos os números reais. Abaixo está um análogo do código em R com seu resultado, mostrando como isso deve ser contado na realidade. A propósito, você tem algumas funções CDF discretas contando corretamente e outras não.

2) Para o valor 1, você obtém um erro de divisão por zero.

[Renat Fatkhullin]

Aleksey Nikolayev:

1) Qualquer CDF - função de distribuição de probabilidade (as discretas não são exceção!) DEVE DEFINITIVAMENTE ser definida para todos os números reais. Abaixo está um análogo do código em R com seu resultado mostrando como isso deve ser considerado na realidade. A propósito, algumas funções CDF discretas foram contadas corretamente e outras não.

2) Para o valor 1, você obtém um erro de divisão por zero.

Leia o código da função e sua verificação, que está no código-fonte.

Como não tenho o R em mãos, terei de verificá-lo separadamente. Estou vendo a divisão por zero, precisamos entender as condições de limite.

[Aleksey Nikolayev]

Renat Fatkhullin:

Devido a um K grande (28), o long de 64 bits foi transbordado ali. O valor de retorno é long.

Para contar valores dentro desses limites, você deve reescrever a função para valores duplos.

Isso está claro. Só que há um erro com o logaritmo do coeficiente binomial com argumentos inteiros e eu pensei que esse fosse o motivo. Agora, dei uma olhada no código e percebi que estava errado - o motivo é outro.

#include <Math\Stat\Math.mqh>

void OnStart()
  { Print(MathBinomialCoefficientLog(62,28));
    Print(MathBinomialCoefficientLog(62.0,28.0));
  }

resultado:

test_clog (EURUSD.m,MN1) -nan(ind)

test_clog (EURUSD.m,MN1) 40.39561099351077

PS: Errado, o problema também está no overflow

[Aleksey Nikolayev]

Renat Fatkhullin:

Não há nenhum R à mão,

R online

[Denis Kirichenko]

Alguns problemas com o NoncentralBeta. Peguei o script da documentação.

Estes são os resultados para diferentes parâmetros.

[Denis Kirichenko]

Fórmula na documentação:

É o análogo na Wikipédia:

Dei uma olhada no código.

A função MathRandomNoncentralBeta() tem linhas como esta:

//--- gerar um número aleatório usando o Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code);
result[i]=chi1/(chi1+chi2);

A mesma Wikipedia tem o seguinte:

The noncentral beta distribution (Type I) is the distribution of the ratio

onde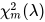 é umavariável aleatória não central qui-quadradocom graus de liberdade m e parâmetro de não centralidade 𝜆 , e 𝜒 𝑛 2 é umavariável aleatória qui-quadrado centralcom graus de liberdade n , independente de 𝜒 𝑚 2 ( 𝜆 ) .

Ou seja, duas variáveis aleatórias são obtidas, sendo a primeira de uma distribuição qui-quadrado não central e a segunda de uma central. Provavelmente o código pode ser corrigido para isso:

//--- gerar um número aleatório usando o Noncentral ChiSquare
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomChiSquare(b2,error_code);
result[i]=chi1/(chi1+chi2);

Os gráficos modificados no exemplo estarão abaixo.