
ピボット平均オシレータの開発:累積移動平均の新規インジケータ
もくじ
イントロダクション: なぜもう一つのオシレーター?
オシレータは、一般的に中央線の上下または事前定義されたセットレベル内で変動するインジケータのサブクラスを表します。 例えば、中央線がクロスしたり、一定の閾値を超えた場合など、トレードイベントのジェネレータとしてテクニカル分析に広く使用されています。 人気のオシレータは、MACD、RSI、CCI、価格の変化率(モメンタムとも呼ばれる)で、反転を予想しようとする、または主なトレンドを検索するなどの特性を持ちます。
一般に、2つの瞬間的な価格の乖離を計算するオシレータは価格を先行する動作 (RSI、CCI など) を示し、平均に基づくオシレータは遅延動作を示します。 関連する例を挙げて、MACDは2つの平均の間の差を計算するので、先行とラグの両方の特性を示していると考えることができます。このような差のプロットはヒストグラムとして描き、中心線のクロスと相違を見つけやすくします。
にもかかわらず、 すべてのオシレータを使用することには、ダマシシグナルを増加させる相場条件 (特に主要なオシレータの場合) またはリスク/報酬比の大部分を歪める可能性のある急速な相違 (遅延オシレータに対して頻繁に起こるため) があるため、すべてのオシレータを使用するには長所と短所があります。 経験則として、トレーダーは、トレーディングシグナルのより独立した確認だけで、一度に複数のオシレータを見る方が賢明です。
この記事では、ピボット平均オシレータは、オシレータの広大なパノラマを持ち込む試みとして、累積移動平均(CMA)の使用に直接由来する新関数を紹介します。
CMA の側面
統計では、単純MA とも呼ばれる移動平均(MA) は、時系列の直近のn個のデータを平均化した計算結果です。 新しい値が下がると、ファーストインファーストアウト (FIFO) ポリシーに従って最も古い値が削除されます。MAレベルは、下落相場でのサポートや上昇相場でのレジスタンスと解釈できるため、金融設定に役立ちます。
MA は 固定メモリーryバッファに対して、最後に使用可能なデータムよりも古いデータ (および結果的に情報の断片) を破棄する概念的に動作します。 理想的には、このようなバッファを無限に拡張して、現在のデータまでのすべてのデータが計算で考慮されるようにする場合、CMAとなります。
幸いなことに、実際のアプリケーションでは、各単一のデータムを格納するための無限のメモリを割り当てる必要はありません! 実際、CMA は、変数の数を少なくして計算できます (再帰的な定式化が使用されているかどうかによって、詳細については次の図を参照してください)。
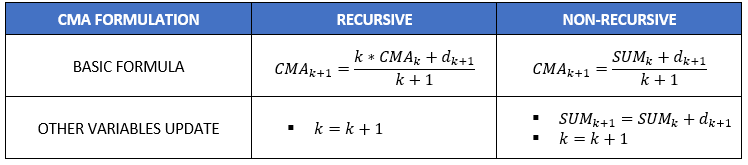
表1:CMAの2つの公式。
CMA 式の 2 番目の興味深い点は、カウンタが 1 単位ずつ増加する点です。 次の CMA 値が、完全に予測可能で、他の情報と補完される要素によって部分的に構成され、予測目的で使用できることを意味します。 例えば、横向きの相場状況では、価格はCMA値に向かってドリフトする傾向があります。
CMAは、以下に提示されるPMOの基本成分です。
PM と PMO の定義
PMO は、直近のデータムと CMA の間の分数として計算される Pivot Mean (PM) と呼ばれる正規化インデックスの上に構築されます。
PM は CMA からの価格の距離を素早く数値的に理解できます。 これは、PMがスプレッドの尺度と考えられることを意味します。 たとえば、PM 値が 1.0035 の場合、現在の値は CMA より 0.35% 高く、PM が 1 に等しい場合は、現在の値が CMA と完全に一致することを意味します。
PM 計算はデータポイントごとに繰り返すことができるため、すべての時系列を PM シグナルに変換できることを意味します。 最終的に、PMO は PM シグナルに適用される 2 つの MA の差として定義されます。 要するに、PMOは2つのスプレッド間の相違の尺度を提供するので、そのアプリケーションをトレード設定に見ると便利です。
PMO の 2 つの平均は、同じ PM シグナルまたは 2 つの異なるシグナルで計算できます。 本稿では、クローズ価格データと始値データから得られるPMシグナルに適用されるシンプルなMAをそれぞれ考察します。

表2:PMおよびPMO式。
類似点がある一方で、ここで提示されたPMO式は、側面についてMACDとは異なります。 MACDは一般的に価格シグナルに適用され、基礎となるPMOシグナルはPMシグナルです。 さらに、MACDでは指数MAが考慮されていますが、ここではSMAに焦点を当て、PMOのより洗練された亜種をこのテーマに関する今後のタスクにします。
基本設計とコード
PMO は、その定式化から直接導出されるインプットをほとんど必要とします。
- 開始時刻: 開始する参照日時
- PM終値シグナルの MA 長:終値から派生した PM シグナルの平均に対するバッファ・データ・ポイント数を表す整数
- PM始値シグナルのMA長:始値から導出された PM シグナルの平均に対するバッファ・データ・ポイント数を表す整数
//--- input parameters input datetime startingTime; input int MA_close=3; input int MA_open=21;
合計で、3 つのバッファを使用します。
- PMO (表示されたインジケータバッファ) 用に 1 つ
- 基礎となる PM シグナルの他の 2 つのシグナル
---インジケータ バッファ double PMOBuffer[]; double closeBuffer[]; double openBuffer[];
グローバル変数に関しては、PMO 計算を可能にする終値と始値の合計を格納するためのカウンタと 2 つの変数が必要です。 また、インプット開始時刻以降のすべてのバッファで使用する最初のインデックスを追跡するために、他のサポート変数もいくつか追加します。
----グローバル変数--- int counter=1; double sum_close=0; double sum_open=0; bool first_val_checked; int first_valid_index;
PMOの2つの平均の計算をサポートするためには、MAを実装する関数を作る必要があります。 避けなければならないのは、開始時間の近くでバッファの先頭で計算が実行される場合です。 その場合、計算に使用できる十分な要素がありません。 ただし、PM定義により、開始時刻の前の値は 1 に設定されていると仮定できるので、MA の微積分にラグを設定することが可能です。 したがって、サポート関数は次のようになります。
double simpleMA(const int pos, const int avg_positions, const double &data[],int arr_tail_pos){ double _local_sum = 0; for(int i=pos+avg_positions-1; i >= pos;i--){ if(i > arr_tail_pos){ _local_sum += 1; // when requested data exceed buffer limit set trailing 1s }else{ _local_sum += data[i]; } } return _local_sum/avg_positions; }
提供されているすべては、最終的にプログラムのコアで見ることができます:
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- ArraySetAsSeries(PMOBuffer,true); ArraySetAsSeries(closeBuffer,true); ArraySetAsSeries(openBuffer,true); ArraySetAsSeries(open,true); ArraySetAsSeries(high,true); ArraySetAsSeries(time,true); //--- return value of prev_calculated for next call int total = rates_total - prev_calculated; double _tmp_sum_close,_tmp_sum_open; if(total > 0){ for(int i=total-1;i>=0;i--){ if(time[i] >= startingTime){ if(first_val_checked == false){ first_val_checked = true; first_valid_index = i; } sum_close += close[i]; sum_open += open[i]; closeBuffer[i] = close[i] *counter / sum_close; openBuffer[i] = open[i]*counter / sum_open; PMOBuffer[i] = simpleMA(i,MA_close,closeBuffer,first_valid_index)-simpleMA(i,MA_open,openBuffer,first_valid_index); counter++; } else{ PMOBuffer[i] = 0; } } }else{ _tmp_sum_close = sum_close +close[0]; _tmp_sum_open = sum_open + open[0]; closeBuffer[0] = close[0] *counter / _tmp_sum_close; openBuffer[0] = open[0] *counter / _tmp_sum_open; PMOBuffer[0] = simpleMA(0,MA_close,closeBuffer,first_valid_index)-simpleMA(0,MA_open,openBuffer,first_valid_index); } return(rates_total); } //+------------------------------------------------------------------+
ユーロドルに関する実験
ここでは、EURUSDチャート上でPMOを実行して得られた実験に関する結果とコメントを提供します。 2 つの主要なトピックについて説明します。
- PMOの使用に関するトレードの側面
- PMO値の分析
トレード面
図が示すように、PMOとRSIの間には強い類似性があります。つまり、2つのシグナルはほぼ一致します。 ただし、いくつか違いもあります。 9月の主要な上昇に近い。 2019年12月(欧州中央銀行の公式通信)に、RSIシグナルと基礎となるEURUSD価格でPMOの"M"メリルパターンを観察することができます。 これは、価格の上昇が9月に起こったという事実によるものです。 CMAに対して相対的に12位は、翌日に観測されたものよりも高かった。 この情報は、2 番目の天井の後にショート ポジションを取る場合に役立つ可能性があります。
RSIとの類似性により、天井とトラフの周りの反転を買われ過ぎや売られ過ぎの条件として考慮することができ、したがってトレード戦略の初期のシグナルとすることができます。 PMOはRSIとして境界付けされていませんが、ゼロ中央線の直線クロスは、トレンドのさらなる確認として考えることができます。 導入で述べたように、一度に複数のシグナルを組み合わせて使用することは、トレードの成功に繋がります。
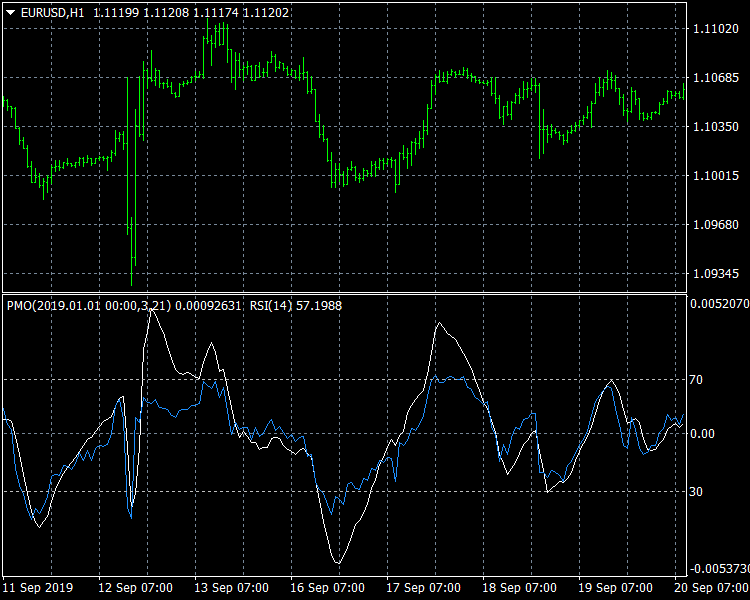
図1: PMO(3,21)とRSI(14)の類似点
PMOとのトレードの基本的でシンプル化されたIF THENルールのセットをスケッチすることができ、PMOベースのEAの未来の開発により洗練された戦略を残すことができます。
- ゼロラインを下回る正の反転の場合、早期買いアラート
- ゼロラインを上回るマイナス反転の場合、早期売りアラート
- もし上向きのゼロラインが続く場合は、買い
- 下向きのゼロラインの場合は、売り
相場の変化する状況に対する迅速な対応は、トレードの成功の重要な要因です。MAを使用するとき、シグナルがスムーズであればあるほど、遅延がおおきくなります。 PMO(m,n)を使用する場合、mはオシレータのラグを占め、nは中央線を横切る際のラグに関連します。 もちろん、PMO で最も速い応答は PMO(1,1) を使用して取得します。 妥協としては、最も速い応答と遅すゼロクロスを保証するn小さい(例えば5)を使用してPMO(1,n)を使用することです。
中心線ゼロの周囲の PMO 値の分布を見ると便利です。 この記事で定義されているように PMO はRSIのように制限されないので、PM 値が特定の閾値を超えるまたは下回る確率を分析するのは興味深いかもしれません。
下の図に、2019年の最初の8ヶ月間に及ぶH1時間枠を持つEURUSDチャートでPMO(3,21)を実行した結果を示します。 PMO 値は、ベル型の分布に従ってゼロを中心に中心に配置されます。 わずかな左のスキューは、おそらく過去数ヶ月でEURUSDによって蓄積されたショート条件によるものです。 にもかかわらず、ゼロの周りの対称性の優位性は、短い動きと長い動きの間に一般的なバランスがあることを推測してみましょう。
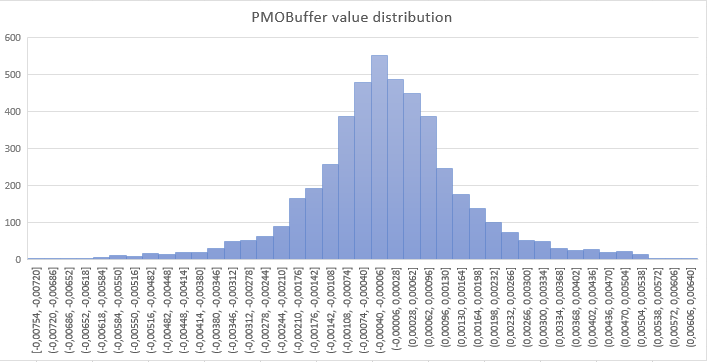
図2:鐘状曲線に似たPMO(3,21)値の分布。 予測目的に役立つ準ガウス統計モデルを考慮
考慮すべきもう一つの側面は、PMOとPMの対応するのではなく、終値と始値シグナルで直接計算された移動平均との関係です。 下の図で報告されているように、Rの正方形との強い相関が近い。 これは、PM シグナルに取り組んでも、基になるシグナルが歪まないことを意味します。 同時に、PM シグナルに対するタスクは、PM 計算によって実行される正規化に、異なるソース (例えば、他の通貨ペア) からの結果を比較する利点があります。
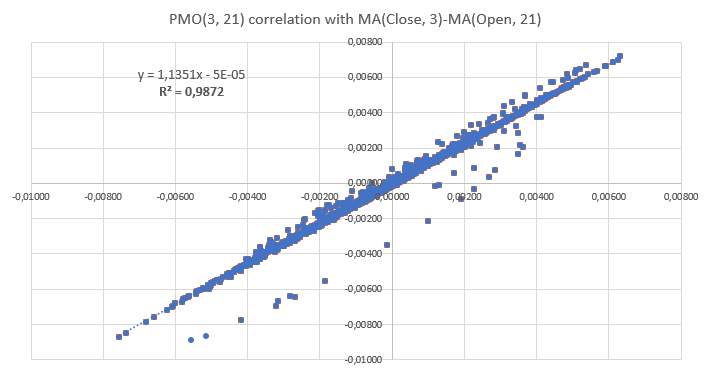
図3: PMO(3,21)と非正規化バージョンとの間に相関が認められました。 得られたほぼ線形形状は、PMOで使用する正規化が、基礎となるオープンおよびクローズ価格シグナルの解釈に大きな歪みを与えないことを示唆します。
結論とさらなるタスク
この記事では、ピボット平均(PM)の新しい概念に基づいてMetaTraderプラットフォームのトレードインジケータとして累積移動平均(CMA)の実装であるピボット平均オシレータ(PMO)を提案しました。 提案されたオシレータは、RSIやMACDのような他の有名なオシレータに似ていますが、CMAの使用から得られる特異性を有することが示されました。 他のタイプの平均に基づく亜種や、ゼロ中心線の周りのPMO値統計分布からの情報を使用するEAなど、さらなる開発の面ではまだ多くの実験が必要です。
添付ファイルを使用して独自の実験を行うことをお勧めします。
添付ファイル
| ファイル | 詳細 |
|---|---|
| PMO.mq4 | 本稿で使用されているPMOのMQL4ソースコード。 |
| PMO_logger.mq4 | データ分析用のログ関数関数を備えたPMOのMQL4ソースコード。 data_logging (true/false フラグ) とファイル名 (文字列) の 2 つの追加インプットの実装 |
| PMO.mq5 | PMOのMQL5ソースコード。 |
| PMO_logger.mq5 | データ分析用のログ関数関数を備えたPMOのMQL5ソースコード。 data_logging (true/false フラグ) とファイル名 (文字列) の 2 つの追加インプットの実装 |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/7265
 クロスプラットフォーム グリッドEAの開発(最終パート):収益性を高める方法と多様化
クロスプラットフォーム グリッドEAの開発(最終パート):収益性を高める方法と多様化
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索