Oui, une question intéressante. Ce qui est encore plus intéressant, c'est la vitesse à laquelle le prix croit bouger.
P.S. Que penser de la définition standard de la vitesse (v=(S2-S1)/(t2-t1) ?
P.P.S. Et si vous y attachiez aussi quelque chose comme un calendrier des actualités? Il s'avérera probablement que chaque nouvelle a son propre temps de "réaction violente".
Si vous y réfléchissez, il y a plusieurs options.
1. La différence entre le prix actuel et le prix il y a quelques barres, divisée par le nombre de barres.
2. Avant de passer du point 1 au point 2, le prix peut avoir oscillé, c'est-à-dire que sa vitesse sera en fait plus élevée qu'au point 1. Nous devons donc calculer la longueur de la trajectoire du prix et la diviser par le nombre de barres. La somme des valeurs absolues de la différence de prix sur une barre divisée par le nombre de barres.
Si vous voulez déterminer la vitesse dans une barre, vous pouvez utiliser le nombre de ticks. Volume[0]/(TimeCurrent()-Time[0]).
4. On peut probablement inventer quelque chose d'autre.
L'auteur du livre le pense-t-il vraiment ? Ce sont des manuels comme celui-ci qui font perdre aux gens tout intérêt pour les mathématiques, la physique et les sciences exactes.
Il semble s'agir d'une mécanique théorique en guise d'introduction. En ce qui concerne le sujet, la variante avec l'utilisation de volumes de tics me semble la plus prometteuse.
Si vous y réfléchissez, il y a plusieurs options.
1. La différence entre le prix actuel et le prix il y a quelques barres, divisée par le nombre de barres.
2. Avant de passer du point 1 au point 2, le prix peut avoir oscillé, c'est-à-dire que sa vitesse sera en fait plus élevée qu'au point 1. Nous devons donc calculer la longueur de la trajectoire du prix et la diviser par le nombre de barres. La somme des valeurs absolues de la différence de prix sur une barre divisée par le nombre de barres.
Si vous voulez déterminer la vitesse dans une barre, vous pouvez utiliser le nombre de ticks. Volume[0]/(TimeCurrent()-Time[0]).
4. On peut probablement inventer quelque chose d'autre.
Je viens de terminer le premier message. Il s'avère que v=s/t. L'auteur du livre est-il vraiment sérieux ? Ce sont des manuels comme celui-ci qui font perdre aux gens tout intérêt pour les mathématiques, la physique et les autres sciences exactes.
Réaction étrange...
.
C'est juste un article d'un manuel de physique.
Ce n'est pas le nombre de ticks mais le nombre de points (pips) parcourus qui doit être compté.
C'est également possible. C'est possible, personne n'interdit rien. Je voulais dire l'hypothèse que le prix se déplace de 1 pip par tick.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation

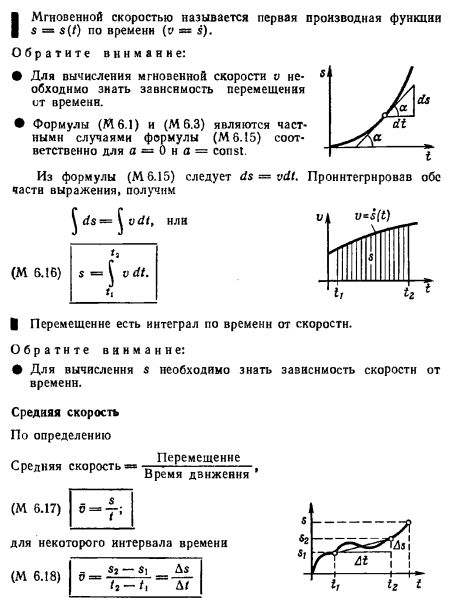

Je voulais demander à la communauté qui calcule la vitesse de variation des prix.
La plupart du temps, ce sont des chandeliers d'actualité.
Une application est l'action de l'EA lorsqu'il y a un fort changement de prix sur une courte période de temps.
Par exemple : Une forte nouvelle est annoncée, et il est judicieux soit de supprimer le TP - et d'en fixer un nouveau pour la situation, soit de déplacer le TP suffisamment loin.
Parce qu'il est ennuyeux d'obtenir une prise de 20-30 100 pips et de regarder ensuite le prix faire 5-10 ou 20 prises de distance supplémentaires.