Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
>> OK. Aquí están los datos.Parece que nos hemos entendido mal. Mi opinión sobre la anormalidad no se aplica al generador, sino al mercado. Construya una distribución de primeros incrementos y compruébelo usted mismo.
Bueno, para el caballo esférico en el vacío, es decir, para una distribución normal garantizada, sí, es poco probable. Los verdaderos no son caballos en el vacío. Hay 5 o 6 s.c.e. e incluso 10.
Tío, por favor, aquí hay otra foto ahora de la libra de 1971, los diarios. Puede haber una sola embestida (y no la hay por cierto :), lo más importante es que no se convierta en un patrón. ¿Verdad?
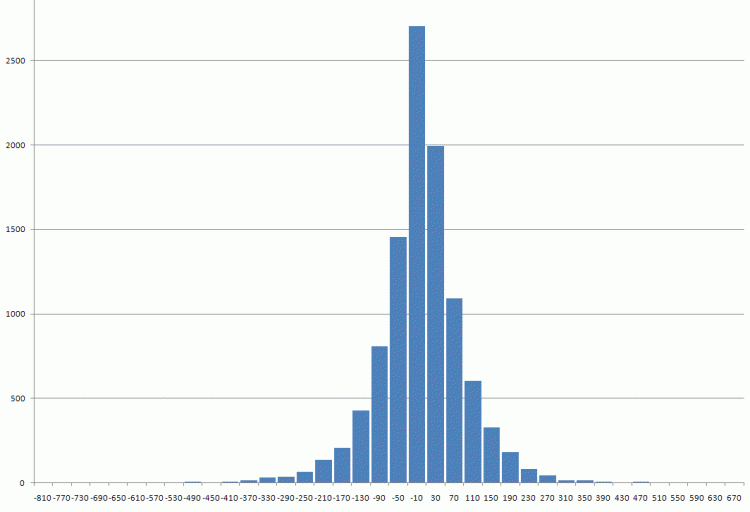
Se adjuntan los datos para su comprobación.Primeras diferencias de libras desde 1971.
>>S. Tal vez habría que comprobar su estacionariedad :)
Tío, por favor, aquí hay otra foto ahora de la libra de 1971, los diarios. Puede haber una sola embestida (y no la hay por cierto :), lo más importante es que no se convierta en un patrón. ¿Verdad?
Se adjuntan los datos del cheque.Las primeras diferencias en la libra desde 1971
Yo lo llamaría una distribución de Laplace a ojo.
Yo la llamaría la distribución de Laplace a ojo
La clave es que no hay 5-6-10 sigmas. Si no, sí, pero hay que probarlo. Y, sin embargo, podría estar bien.Ilya, aquí tienes una sugerencia: aproxima esta distribución por una distribución normal. Y a continuación, vea la diferencia entre el histograma real y la aproximación de la curva de Gauss. No te limites a tres sigmas, busca al menos diez.
Otra comprobación trivial: calcular los primeros momentos de esta distribución y compararlos con los momentos de la distribución normal.
El fenómeno de las colas gruesas en las series financieras es conocido desde hace tiempo. ¿Qué quieres demostrarme?
Ilya, aquí tienes una sugerencia: aproxima esta distribución por una distribución normal. Y a continuación, vea la diferencia entre el histograma real y la aproximación de la curva de Gauss. No te limites a tres sigmas, busca al menos diez.
Otra comprobación trivial: calcular los primeros momentos de esta distribución y compararlos con los momentos de la distribución normal.
El fenómeno de las colas gordas en las series financieras es conocido desde hace tiempo. ¿Qué quieres demostrarme?
La charla fue sobre 5-6-10 RMS. No veo un patrón en su apariencia.
La clave es que no hay 5-6-10 sigmas. Tal como está, sí, pero hay que probarlo. Y, sin embargo, podría ser normal.es muy poco probable que sea así. Las distribuciones normales suelen encontrarse en la naturaleza, donde una variable aleatoria "grande" es la suma de un gran número de variables aleatorias "pequeñas" distribuidas de una forma determinada (pero igual). Un ejemplo paradigmático es el movimiento browniano, al que ya se han dedicado muchas páginas en el siguiente hilo. En el caso del mercado, la ley de formación de los precios dista mucho de serlo, ya que para conseguir una normal se necesita un número muy elevado de "perturbaciones" externas, que deben ser el factor principal en la formación de la distribución. Pero no creemos que los precios en el mercado sean ruido, ¿verdad?
En un gráfico, puramente visual, y no verás ese 5-6-10.
En algún lugar tenía incluso un gráfico que mostraba las diferencias. Si se toman los dos primeros momentos de la distribución y se piensa en ellos como momentos de aproximación a la normal, la diferencia de frecuencias en 3, 4, 5, etc. sigmas es fácil de calcular.
No recuerdo las cifras exactas, pero la frecuencia de desviación real de 3 sigmas es 3-4 veces mayor que la gaussiana (gaussiana 0,3%, real más del 1%). La desviación de 4 sigmas se produce en la realidad con más frecuencia que la gaussiana en unas 15 veces. Para 5 sigmas la diferencia es de decenas de veces, si no de cientos. Y así sucesivamente.
Mientras no se evalúen los riesgos, no importa si es gaussiano o no.
P.D. Por cierto, parece que, según Taleb, LTCM se hundió precisamente por subestimar los riesgos. Una desviación de 10 sigmas se consideró un evento raro insignificante. Y eso es exactamente lo que ocurrió.
No recuerdo las cifras exactas, pero la frecuencia de desviación real de 3 sigmas es 3-4 veces la gaussiana (gaussiana 0,3%, real más del 1%). La desviación de 4 sigmas se produce en la realidad con más frecuencia que la gaussiana en unas 15 veces. Para 5 sigmas la diferencia es de decenas de veces. Y así sucesivamente.
...lo que una vez más es una prueba a favor de Laplace.
Mientras no se evalúen los riesgos, no importa si es gaussiano o no.
¿Puede decirme cómo enfocar la evaluación de riesgos?