Esto es fundamentalmente erróneo.
En primer lugar, hablemos en ruso y llamemos "curtosis" e "insularidad" con el término aceptado: coeficiente de curtosis o simplemente curtosis.
En segundo lugar, la "insularidad" y las "colas gordas" en general no tienen ninguna relación. He aquí un contraejemplo: la distribución de Laplace ( exponencial bilateral), a la que, todo sea dicho, obedecen los gráficos de la inmensa mayoría de las series temporales financieras. Su exceso es igual a 3 (es decir, su parte superior es más aguda que la de la distribución normal), pero las colas son gruesas: disminuyen según la ley exp(-x), es decir, más lentamente que la de la gaussiana exp(-x^2).
Es fundamentalmente erróneo.
En primer lugar, hablemos en ruso y llamemos "curtosis" e "insularidad" con el término aceptado: coeficiente de curtosis o simplemente curtosis.
En segundo lugar, la "insularidad" y las "colas gordas" en general no tienen ninguna relación. He aquí un contraejemplo: la distribución de Laplace (exponencial bilateral), a la que, todo sea dicho, obedecen los gráficos de la inmensa mayoría de las series temporales financieras. Su exceso es igual a 3 (es decir, la parte superior es más aguda que en la distribución normal), pero las colas son simplemente gruesas: disminuyen según la ley exp(-x), es decir, más lentamente que en la gaussiana exp(-x^2).
Además, no existe el concepto de "Exceso" propiamente dicho, existe el concepto de "Coeficiente de Exceso", que es una medida para otro concepto "Exceso de Distribución", y este concepto sólo se define para distribuciones unimodales. Así pues, para utilizar correctamente este coeficiente es necesario, en primer lugar, determinar la función de distribución empírica, lo que no es una tarea trivial desde el punto de vista de las matemáticas, y en segundo lugar, en el marco de algunos criterios probabilísticos, comprobar y aceptar la hipótesis de que la distribución tiene una sola moda, lo que no siempre se cumple en el caso de las series financieras y también es una tarea no trivial. Sin estos pasos el cálculo posterior es imposible, si requiere el "Coeficiente de exceso".
P.D..
No hay nada escrito sobre qué hacer si el test dice que la serie no es aplicable para el modelo supuesto.
Nada se dice sobre por qué y en base a qué se utiliza una serie de los llamados "rendimientos" y no otra.
En la práctica, la principal razón por la que es preferible trabajar con rendimientos de activos que con precios directos de activos es que los rendimientos tienen propiedades estadísticas más atractivas.
alsu:
...Hablemos en ruso y llamemos "curtosis" e "insularidad" por el término aceptado - coeficiente de exceso o simplemente exceso....
Me ha gustado especialmente el hecho de que alsu considere rusas las palabras "coeficiente" y "exceso"...
alsu:
En segundo lugar, la "insularidad" y las "colas gordas" no suelen estar relacionadas. He aquí un contraejemplo: la distribución de Laplace (exponencial bilateral), a la que, cabe señalar, obedecen los gráficos de la inmensa mayoría de las series temporales financieras. Su exceso es igual a 3 (es decir, la parte superior es más aguda que en la distribución normal), pero las colas son simplemente gruesas - decrecen según la ley exp(-x), es decir, más lentamente que en la gaussiana exp(-x^2).
Eso es exactamente lo que creo que está relacionado en general.
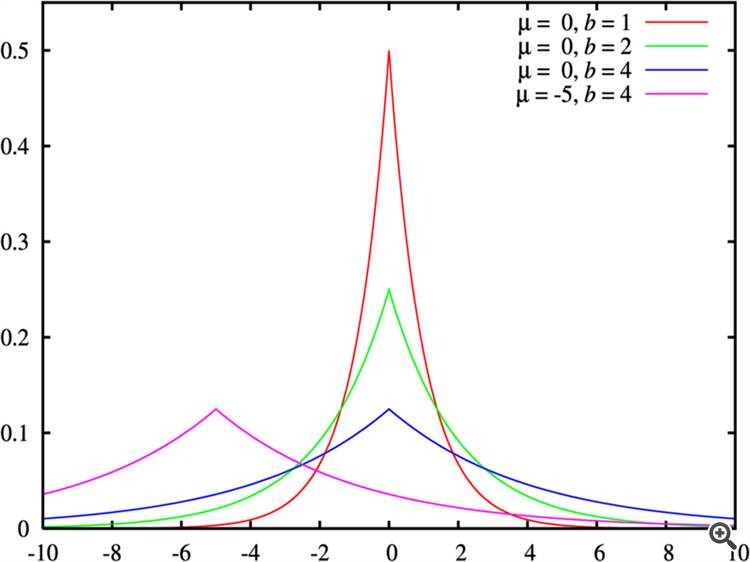
Un ejemplo de "menos curtosis-colas más gruesas" se muestra en la Fig. "Distribuciones de Laplace con diferentes parámetros".
Sólo añadiría la siguiente frase a mi artículo: "La distribución de una serie de rendimientos muestra más a menudo un comportamiento de colas gordas que la distribución normal". El fenómeno de las "colas gordas" se denomina exceso de curtosis en la literatura anglosajona. Las series cuyas distribuciones presentan este tipo de colas se denominan leptocúrticas, es decir, que tienen una curtosis positiva (superior a la curtosis de la distribución normal).
A continuación, sobre el coeficiente de cur tosis:
Ladistribución normal tiene curtosis cero, γ2 = 0.
Si las colas de la distribución son más "ligeras" y el pico es más agudo que el de la distribución normal, entonces γ2 > 0.
Si las colas de la distribución son más "pesadas" y el pico es más "aplanado" que la distribución normal, entonces γ2 < 0.
Sólo añadiría esa sugerencia a mi artículo:
Sólo añadiría la siguiente frase a mi artículo: "La distribución de una serie de rendimientos muestra más a menudo un comportamiento de colas gordas que la distribución normal". El fenómeno de las "colas gordas" se denomina exceso de curtosis en la literatura anglosajona. Las series cuyas distribuciones presentan este tipo de colas se denominan leptocúrticas, con curtosis positiva (superior a la curtosis de la distribución normal).
A continuación, sobre el coeficiente de cur tosis:
Ladistribución normal tiene curtosis cero, γ2 = 0.
Si las colas de la distribución son más "ligeras" y el pico es más agudo que el de la distribución normal, entonces γ2 > 0.
Si las colas de la distribución son "más pesadas" y el pico es más "aplanado" que la distribución normal, entonces γ2 < 0.
Mientras discutís sobre términos, yo de la noche a la mañana ya he construido algunos EAs rentables usando ideas de este artículo. :-)
Sin embargo, sus beneficios son muy pequeños, aunque son bastante estables (comprobado en el historial de 12 años, los gráficos crecen maravillosamente). Las correlaciones detectadas por los métodos descritos en el artículo son bastante débiles ( los coeficientes de autocorrelación de las series son de alrededor de 0,01, en casos excepcionales acercándose a 0,1, dependiendo de qué derivados de precios estén correlacionados), y al operar el beneficio de ellos es fuertemente batido por el spread. Tuve que añadir un filtro para hacer operaciones sólo a la llegada de señales fuertes, de lo contrario la curva de rentabilidad bajaría casi en línea recta.
Gracias al autor en cualquier caso. Las ideas son valiosas. Creo que los críticos no deberían meter las narices del autor en los abismos de la matemática, sino considerar el artículo como una indicación de un amplio campo para experimentos prácticos.
Mientras discutís sobre términos, yo de la noche a la mañana ya he construido algunos EAs rentables usando ideas de este artículo. :-)
Sin embargo, sus beneficios son muy pequeños, aunque son bastante estables (comprobado en el historial de 12 años, los gráficos crecen maravillosamente). Las correlaciones detectadas por los métodos descritos en el artículo son bastante débiles (los coeficientes de autocorrelación de las series son de alrededor de 0,01, en casos excepcionales acercándose a 0,1, dependiendo de qué derivados de precios estén correlacionados), y al operar el beneficio de ellos es fuertemente batido por el spread. Tuve que añadir un filtro para hacer operaciones sólo a la llegada de señales fuertes, de lo contrario la curva de rentabilidad bajaría casi en línea recta.
Gracias al autor en cualquier caso. Las ideas son valiosas. Creo que los críticos no deberían meter las narices del autor en los abismos de la matemática, sino considerar el artículo como una indicación de un amplio campo para experimentos prácticos.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Análisis de los gráficos mediante métodos econométricos:
En este artículo se describen los métodos econométricos de análisis, el análisis de la correlación y el análisis de la varianza condicional en particular. ¿Cuáles son les beneficios del método descrito en este artículo? El uso de los modelos GARCH no lineales permite la representación formal de las series analizadas desde un punto de vista matemático y crear predicciones para un número determinado de pasos.
Autor: Dennis Kirichenko