Discussing the article: "Algorithmic Trading Strategies: AI and Its Road to Golden Pinnacles"

[MetaQuotes]

Check out the new article: Algorithmic Trading Strategies: AI and Its Road to Golden Pinnacles.

This article demonstrates an approach to creating trading strategies for gold using machine learning. Considering the proposed approach to the analysis and forecasting of time series from different angles, it is possible to determine its advantages and disadvantages in comparison with other ways of creating trading systems which are based solely on the analysis and forecasting of financial time series.

The evolution of understanding the capabilities of machine learning methods in trading has resulted in the creation of different algorithms. They are equally good at the same task, but fundamentally different. This article will consider a unidirectional trending trading system again in the case of gold, but using a clustering algorithm.

• The previous article described two causal inference algorithms for creating a similar trending strategy for gold.
• The article on time series clustering discussed different ways of clustering in trading tasks.
• The creation of a mean-reversion strategy using a clustering algorithm was presented to the public earlier.
• The development of a clustering-based trend trading system has also highlighted capabilities of this approach.

Considering this important approach to the analysis and forecasting of time series from different angles, it is possible to determine its advantages and disadvantages in comparison with other ways of creating trading systems which are based solely on the analysis and forecasting of financial time series. In some cases, these algorithms become quite effective and surpass classical approaches both in terms of the speed of creation and the quality of trading systems at the exit.

In this article, we will focus on unidirectional trading, where the algorithm will only open buy or sell trades. CatBoost and K-Means algorithms will be used as basic algorithms. CatBoost is a basic model that performs functions of a binary classifier for classifying trades. Whereas, K-Means is used to determine market modes at the preprocessing phase.

Author: dmitrievsky

[[Deleted]]

After reading the article, I had an idea to play with the clustering process itself.

I wrote a variant that performs clustering in a sliding window instead of on the whole dataset. This may improve the partitioning of clusters, taking into account the temporal structure of BP.

def sliding_window_clustering(dataset, n_clusters: int, window_size=200) -> pd.DataFrame:
    import numpy as np
    
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    
    # First we create global reference centroids
    global_kmeans = KMeans(n_clusters=n_clusters).fit(meta_X)
    global_centroids = global_kmeans.cluster_centers_
    
    clusters = np.zeros(len(data))
    
    # Apply clustering in a sliding window
    for i in range(0, len(data) - window_size + 1, window_size):
        window_data = meta_X.iloc[i:i+window_size]
        
        # Teach KMeans on the current window
        local_kmeans = KMeans(n_clusters=n_clusters).fit(window_data)
        local_centroids = local_kmeans.cluster_centers_
        
        # Match the local centroids to the global centroids
        # to ensure consistency of cluster labels
        centroid_mapping = {}
        for local_idx in range(n_clusters):
            # Find the nearest global centroid to this local centroid
            distances = np.linalg.norm(local_centroids[local_idx] - global_centroids, axis=1)
            global_idx = np.argmin(distances)
            centroid_mapping[local_idx] = global_idx + 1  # +1 to start numbering from 1
        
        # Get the labels for the current window
        local_labels = local_kmeans.predict(window_data)
        
        # Convert local labels to consistent global labels
        for j in range(window_size):
            if i+j < len(clusters):  # Checking for out of bounds
                clusters[i+j] = centroid_mapping[local_labels[j]]
    
    data['clusters'] = clusters
    return data

Insert this function into the code and replace clustering with sliding_window_clustering.

It seems to improve the results.

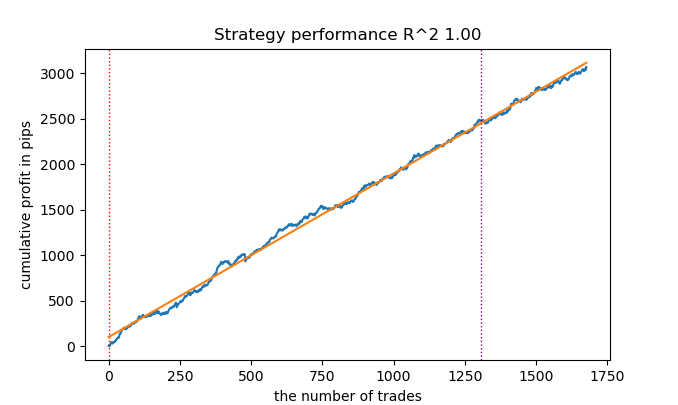
Still, sometimes it is useful to write articles.

[Sun Paul]

Thanks for the article Dmitrievsky. It looks the uploaded EA and its include file are mismatch with each other. It refer the mpq file in the folder "Trend following"， but the sample files were in "Mean reversion".
And the function get_features in the "causal one direction.py" are not the same as what appears in the article. Besides that, the mqh file generated by "causal one direction.py" when exporting .onnx is not the same as what offered in MQL5_files.zip.

Very appriciate if you can make necessary clarification.

Paul

[[Deleted]]

Sun Paul #:

Thanks for the article Dmitrievsky. It looks the uploaded EA and its include file are mismatch with each other. It refer the mpq file in the folder "Trend following"， but the sample files were in "Mean reversion".
And the function get_features in the "causal one direction.py" are not the same as what appears in the article. Besides that, the mqh file generated by "causal one direction.py" when exporting .onnx is not the same as what offered in MQL5_files.zip.

Very appriciate if you can make necessary clarification.

Paul

Thanks, I'll check and re-upload, maybe I mixed up some files.

[[Deleted]]

Updated the archives + added a new clustering method.

Now all paths and functions match.

[Aliaksandr Kazunka]

I think we should add RandomisedSearchCV parameter enumeration for the CatBoost model to select the best parameters. And cross-validation wouldn't hurt. All this improves the accuracy of the model.

[Rashid Umarov]

Maxim Dmitrievsky #:

Updated the archives + added a new clustering method.

Now all paths and functions match.

Uploaded these files to the article

[[Deleted]]

sportoman CatBoost model to select the best parameters. And cross-validation wouldn't hurt. All this improves the accuracy of the model.

You get randomness multiplied by randomness. It will be hard to reproduce, then you need to fix seed everywhere.

Usually a few re-training in a loop is enough to evaluate the strategy.

[Aliaksandr Kazunka]

So you have R2 is a modified index, the efficiency of which is based on the profit in pips. What about drawdown and other performance indicators? If we get a model that gives more than 90% on training and at least 85% on the test, then your index will give impressive figures. No matter how many times I have run the tester on MT5, I have never received a profit on the history. The deposit is drained. This is despite the fact that your tester on Python gives out 0.97-0.98

[[Deleted]]

sportoman #:
So you have R2 is a modified index, the efficiency of which is based on the profit in pips. What about drawdown and other performance indicators? If we get a model that gives more than 90% on training and at least 85% on the test, then your index will give impressive figures. No matter how many times I have run the tester on MT5, I have never received a profit on the history. The deposit is drained. This is despite the fact that your tester on Python gives out 0.97-0.98

I don't understand what this has to do with CV.

All these strategies have low proving power, because they are based only on the history of non-stationary quotes. But you can catch trends.

Any double-checking on history does not increase the odds if the trends change. That is, you cannot prove something about the future based on history, you can only estimate how well the model generalises on the available data. There is a test period for that.

If some new efficient way of testing models on non-stationary series has already been invented, please let me know :).

[[Deleted]]

There is also an article on mean reversion strategies. There we make the stronger assumption that a time series returns to the mean almost always. Unlike trends, which change.