Greetings, traders. My relentless quest for innovative solutions led me to a scientific article discussing a groundbreaking technology - the integration of Quantum Machine Learning (QML) and the Nuclear Norm Maximization Method (NNM) in trading.Inspired by the potential of this innovation, I embarked on extensive research and conducted numerous experiments. Ultimately, I developed a unique strategy that harnesses the advantages of QML and NNM for analyzing stock market charts and making trades based on more intricate and precise models than what a human analyst could achieve.With the help of machine learning algorithms, I trained the system to uncover hidden patterns and low-rank structures in financial data using QML. This enabled us to make more accurate forecasts and significantly boosted confidence in this strategy.However, my innovative approach doesn't solely rely on QML. The NNM method plays a pivotal role in processing financial data. It aids in detecting and filling missing values while efficiently filtering out noise and mitigating the impact of anomalies on the original data.This led me to create The Legend EA advisor, a powerful tool that applies QML and NNM to make decisions in the Forex market. Thanks to these cutting-edge technologies, it has become a significant player in financial markets, providing real-time visualization of analysis directly on trading charts.My trading strategy is built on complex computer analysis that goes beyond the capabilities of human analysis. Today, The Legend EA is widely recognized as one of the most successful advisors in the Forex market.My unwavering determination and investigative approach have led to the development of a revolutionary strategy that has transformed the trading landscape. I hope that The Legend EA will serve as a source of inspiration for those facing challenges in trading, as there are always new opportunities to explore through innovation and persistence.
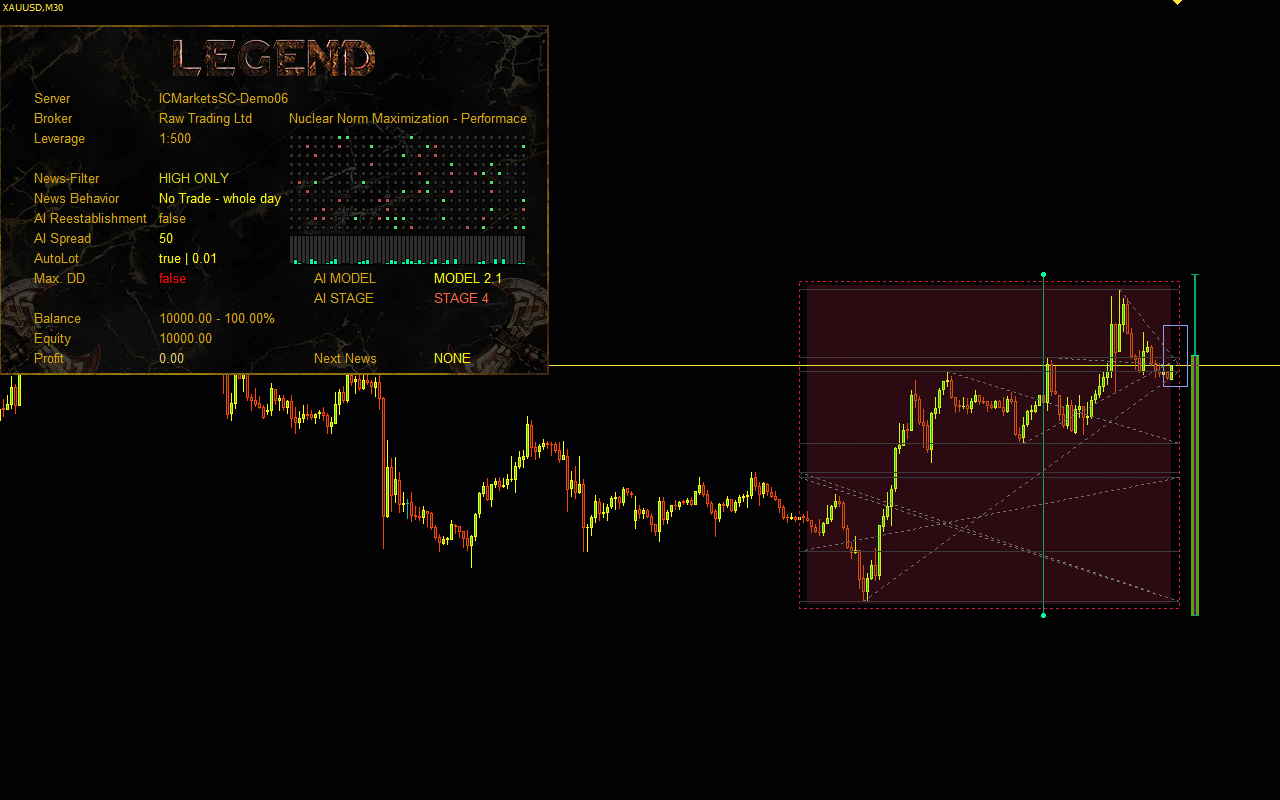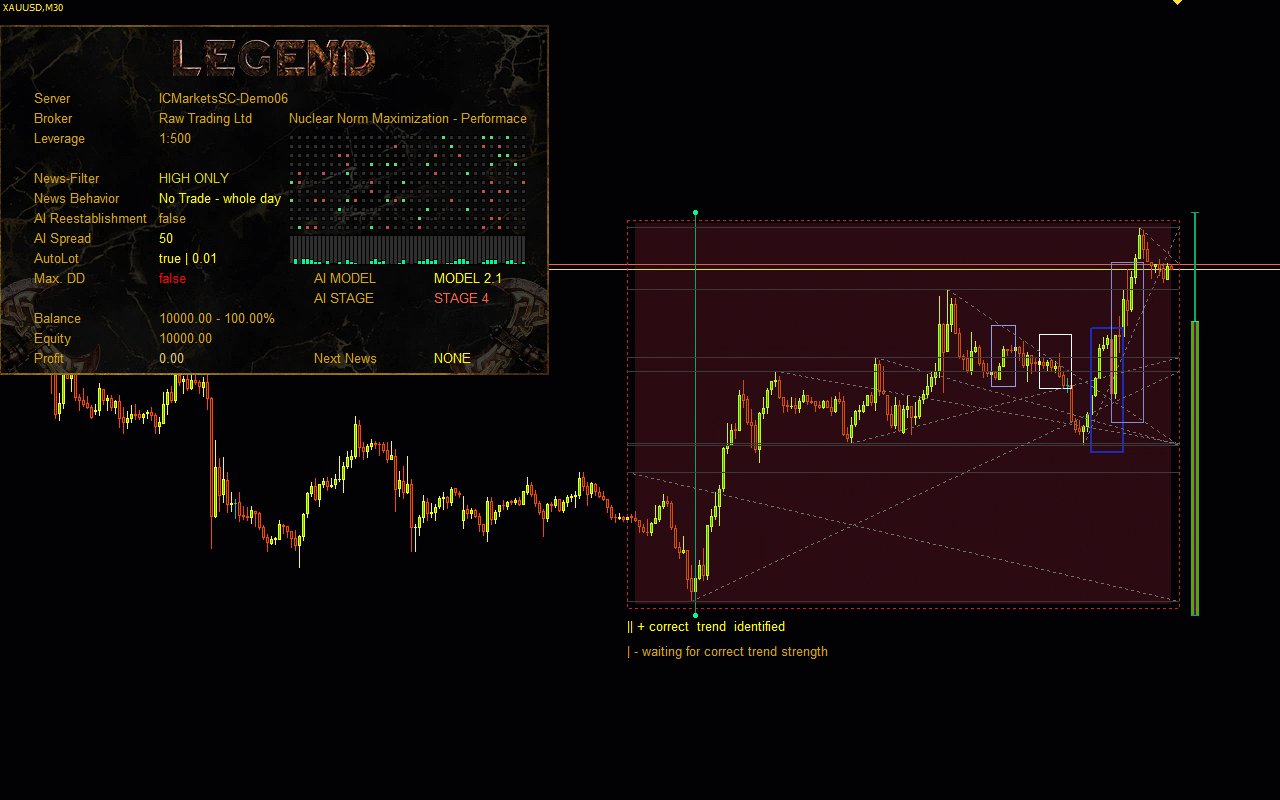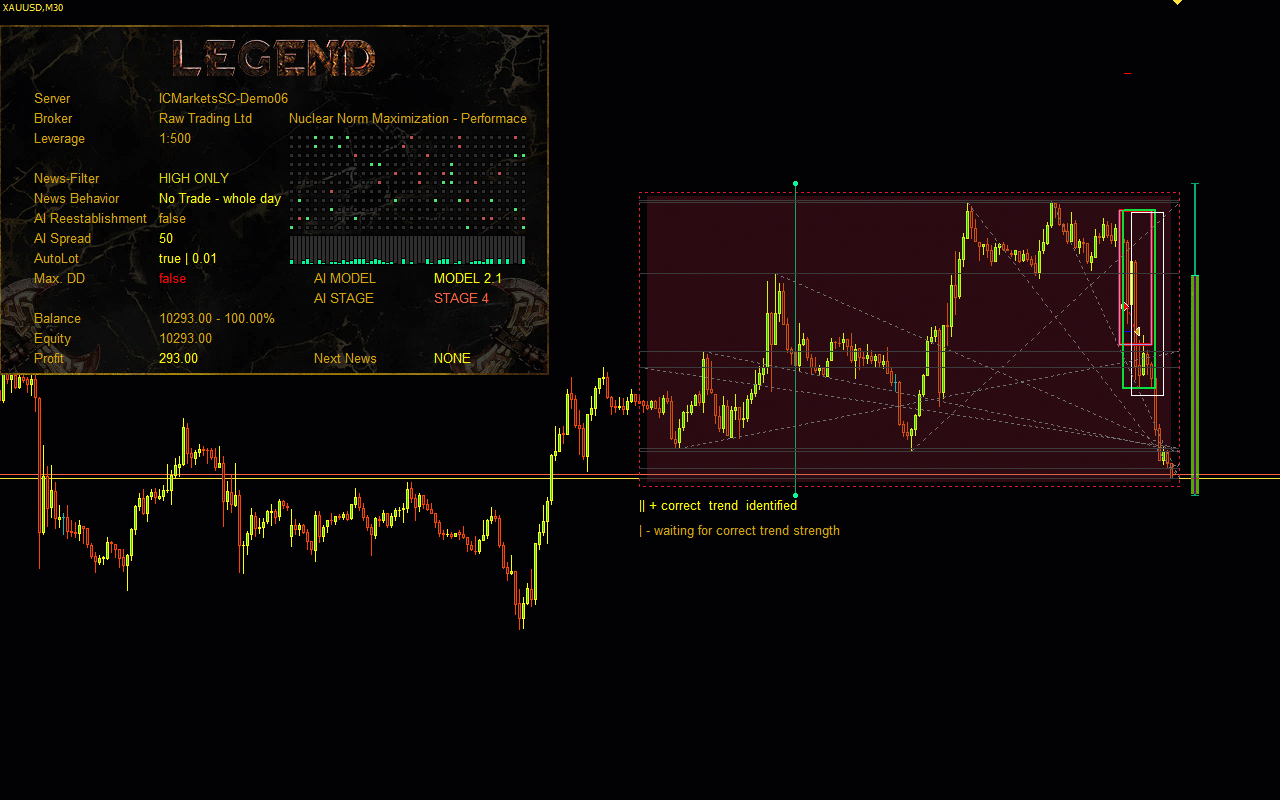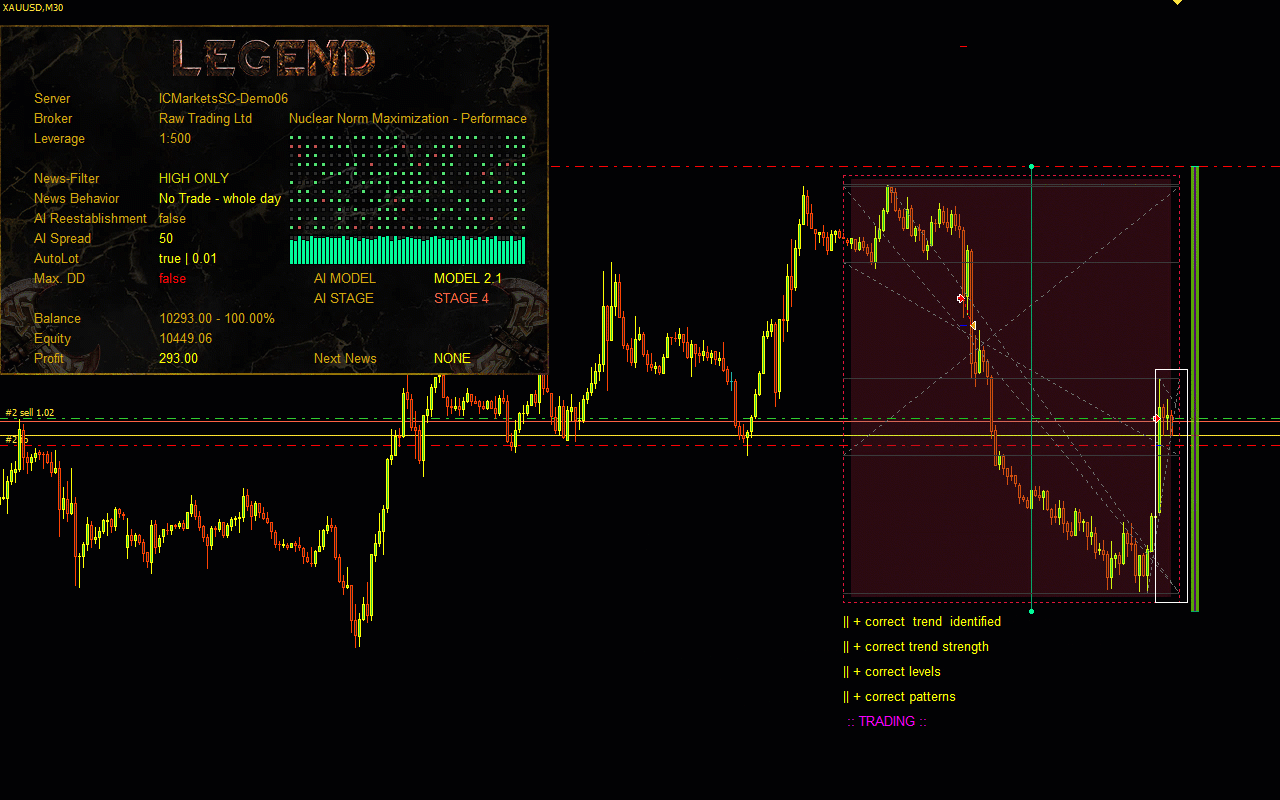
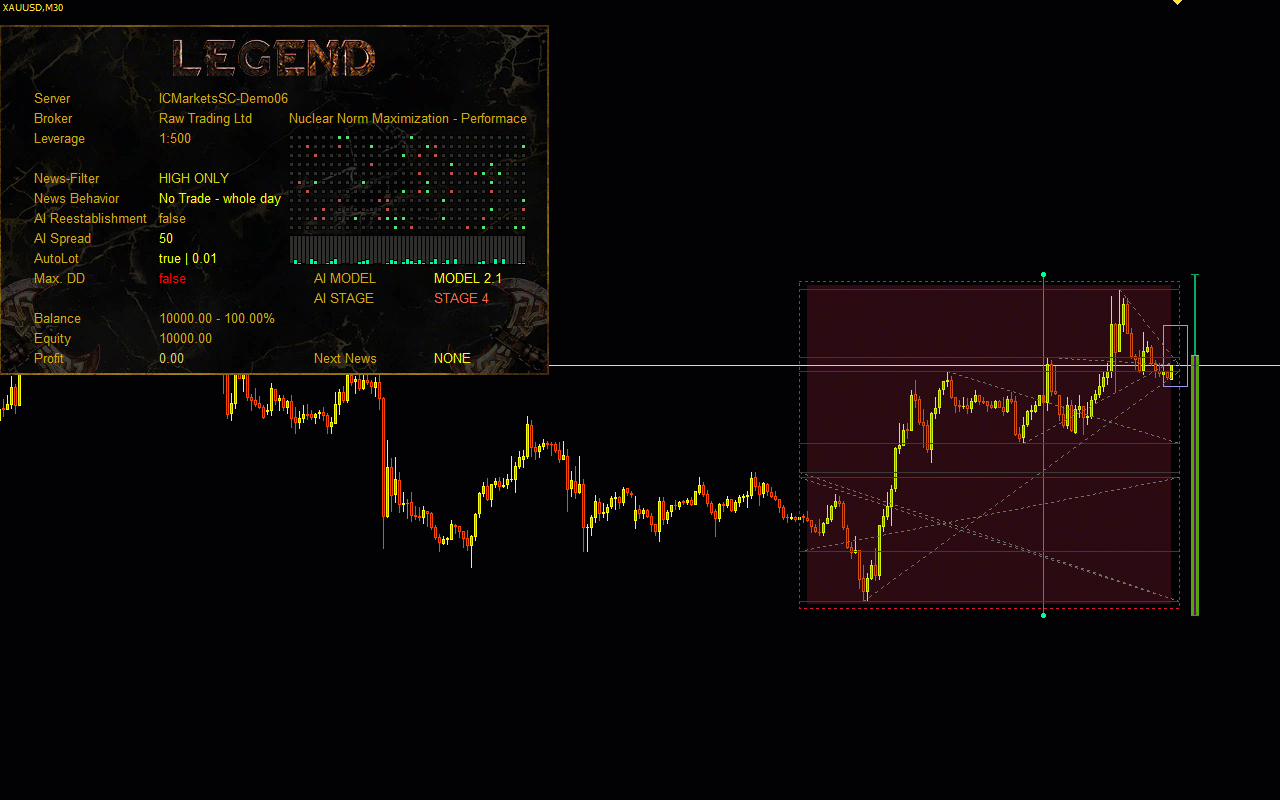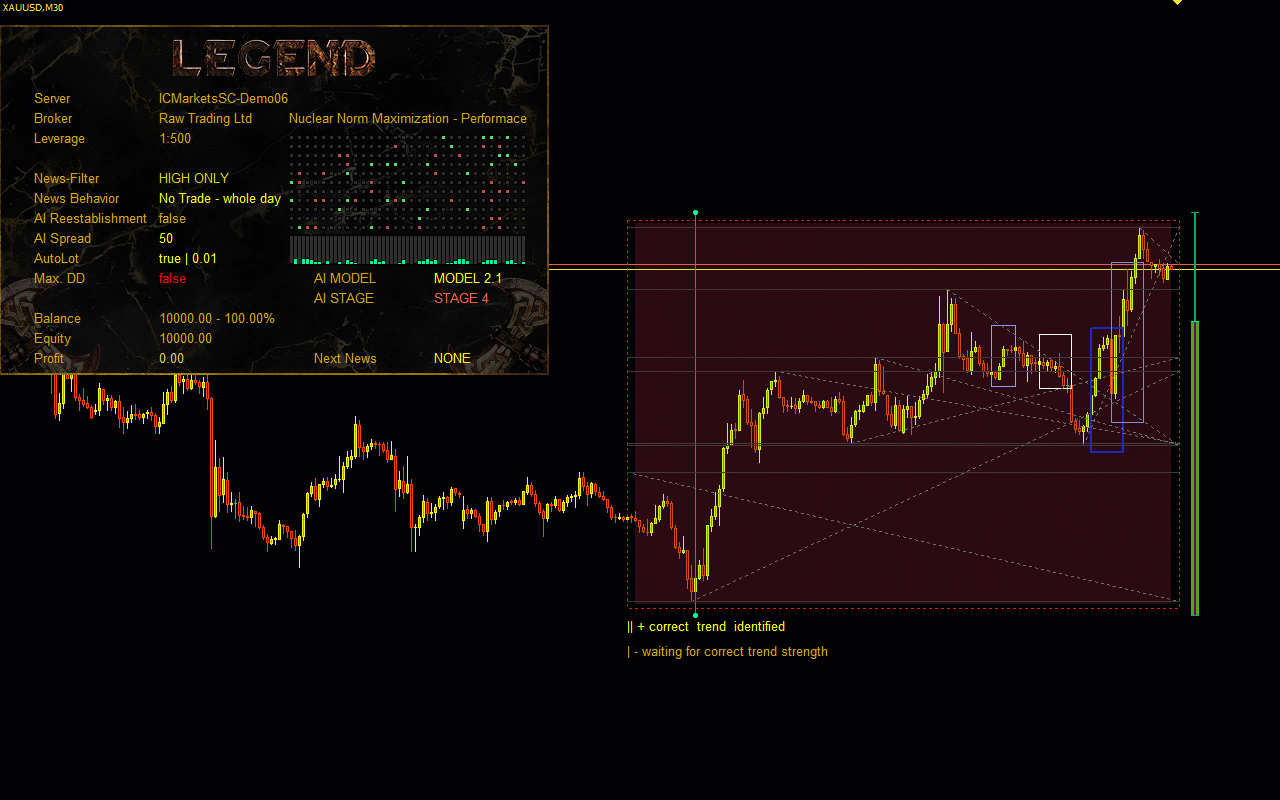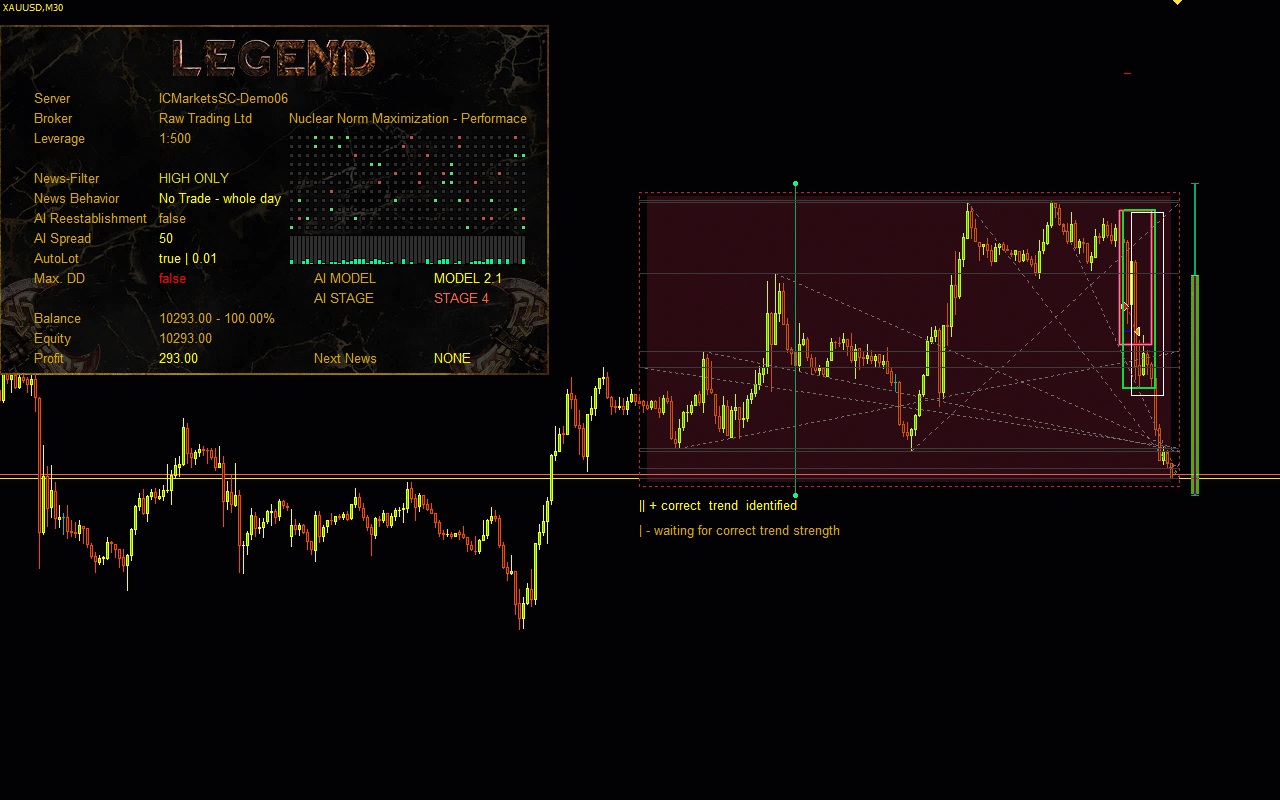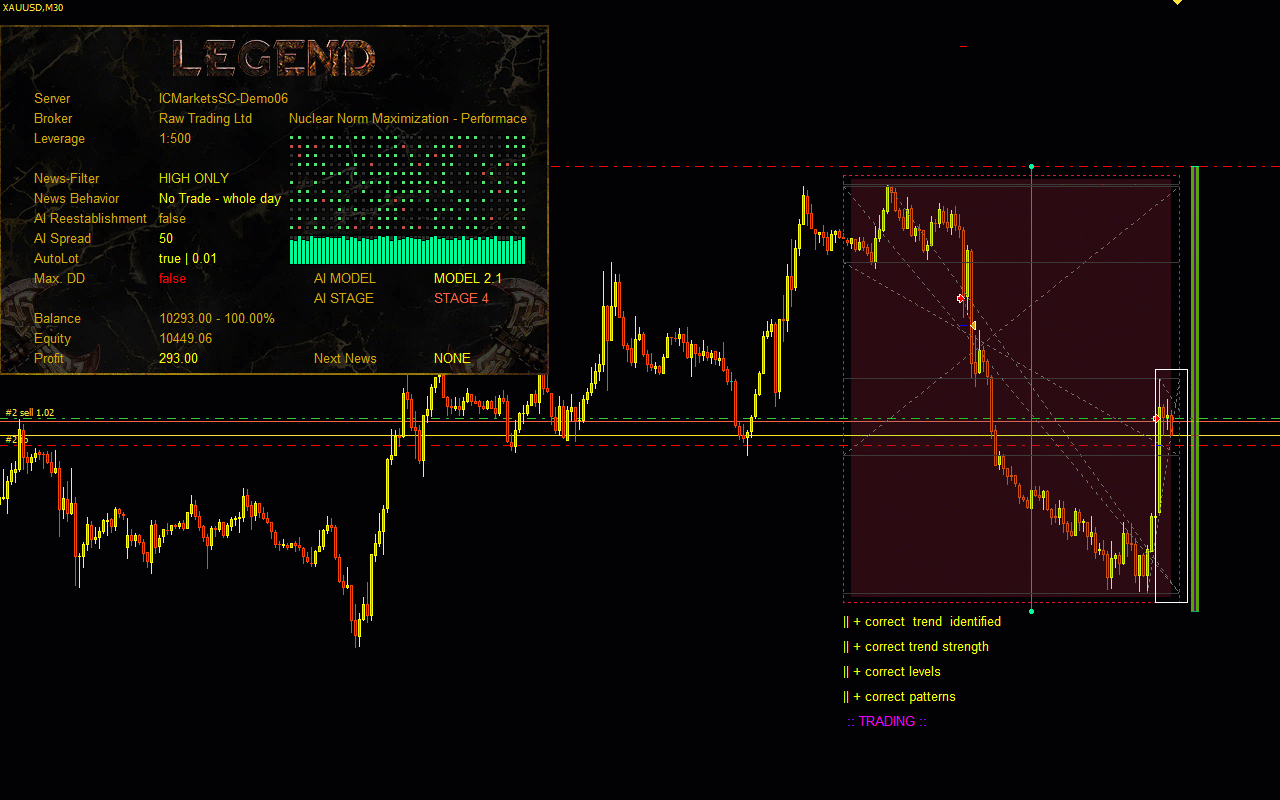
Visualisation of the Nuclear Norm Maximization method.
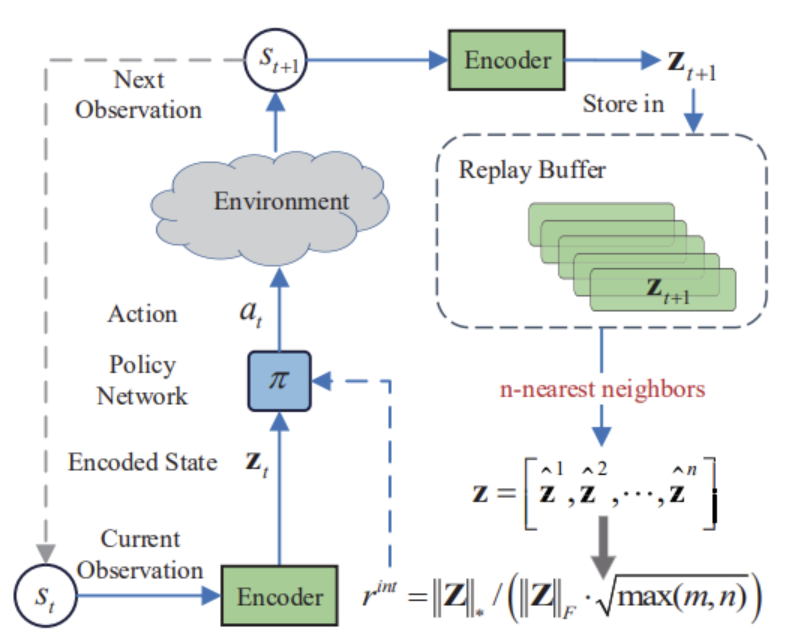
In this project, we are introduced to a novel approach to stimulating exploration in reinforcement learning based on maximising the nuclear norm. This method can efficiently estimate the novelty of a trade process study by considering historical information and providing high robustness to noise and outliers.In the practical part of the paper, I integrated the Nuclear Norm Maximisation method into the RE3 algorithm. I trained the model and tested it in MetaTrader 5 strategy tester. According to the test results, we can say that the proposed method has significantly diversified the Actor's behaviour, compared to the results of training the model using the pure RE3 method.


QML Framework
The basic "building block" in QML is the Variational Quantum Circuit. Basically QML is built using a "hybrid" scheme, where we have parameterised quantum circuits such as VQCs and they constitute the "quantum" part. "Classical" part is usually responsible for optimising the parameters of the quantum circuits, e.g. by gradient methods, so that the VQCs, like layers of neural networks, "learn" the input data transformations we need. This is how the Tensorflow Quantum library is built, where quantum "layers" are combined with classical ones, and learning takes place as in conventional neural networks.

Variational Quantum Circuit
VQC is the simplest element of quantum-classical learning systems. In the minimal variant it represents a quantum circuit which encodes by input data vector $\vec{X}$ a quantum state $\left | {\Psi} {\right >$ and then applies to this state the operators parameterised by the parameters $\theta$. If we draw an analogy with conventional neural networks, we can think of VQC as a kind of "black box" or "layer" that performs the transformation of input data $\vec{X}$ depending on the parameters $\theta$. And then, we can say that $\theta$ is the analogue of "weights" in classical neural networks.This is how the simplest VQS looks like, where the vector $\vec{X}$ is encoded through the rotations of qubits around the axis $\mathbf{X}$, and the parameters $\theta$ encode the rotations around the axis $\mathbf{Y}$.

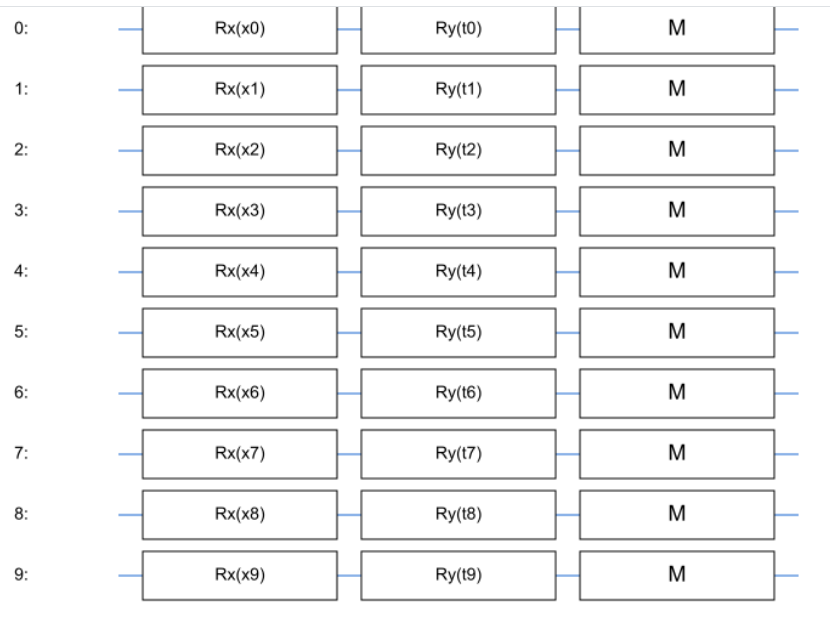
Let's look at this point in more detail. We want to encode the input data vector $\vec{X}$ into the state $\left | \Psi \right >$, in fact, to perform the operation of translation of "classical" input data into quantum data. To do this, we take $N$ qubits, each of which is initially in the $\left | 0 \right >$ state. We can represent the state of each individual qubit as a point on the surface of the Bloch sphere.We can "rotate" the $\left | \Psi \right >$ state of our qubit by applying special one-qubit operations, so-called gates $Rx$, $Ry$, $Rz$, corresponding to rotations with respect to different axes of the Bloch sphere. We will rotate each qubit, for example, along the $\mathbf{X}$ axis by an angle determined by the corresponding component of the input vector $\vec{X}$. Having obtained the quantum input vector, we now want to apply a parameterised transformation to it. For this purpose, we will "rotate" the corresponding qubits along another axis, for example, along $\mathbf{Y}$ by angles determined by the parameters of the $\theta$ circuit.
In the library for quantum computing Cirq from Google, which we will actively use, this can be realised, for example, as follows:

Thus, we obtain a quantum cell - circuit, which is parameterised by classical parameters and applies a transformation to a classical input vector. Quantum-classical learning algorithms are built on such "blocks". We will apply transformations to classical data on a quantum computer (or simulator), measure the output of our VQC and further use classical gradient methods to update the VQC parameters.
Finally and most interestingly, the code to train our VQC on Tensorflow Quantum.


lr here is a parameter responsible for the gradient descent rate and is a hyperparameter.This is the simplest standard learning loop in Tensorflow, and model is an object of class tf.keras.layers.Layer, for which we can apply all our usual optimisers, loggers and techniques from "classical" deep learning. The VQC parameters are stored in a variable of type tf.Variable and are updated using the simple rule $\theta_{k+1} = \theta_k - \gamma \cdot g_k$, this is a minimal implementation of gradient descent at a rate of $\gamma$. We use 5000 measurements each time to estimate as accurately as possible the expected value of our operator $\hat{\mathbf{Op}}$ in the $\left | \Psi(\theta_k) \right >$ state. All of this for 350 epochs. On my laptop for $N = 5$, $j = 1.0$ and $h = 0.5$, the process took about 40 seconds.
Let's visualise the training graphs (scipy gave the exact solution $\simeq -4.47$): tensoboard --logdir train/
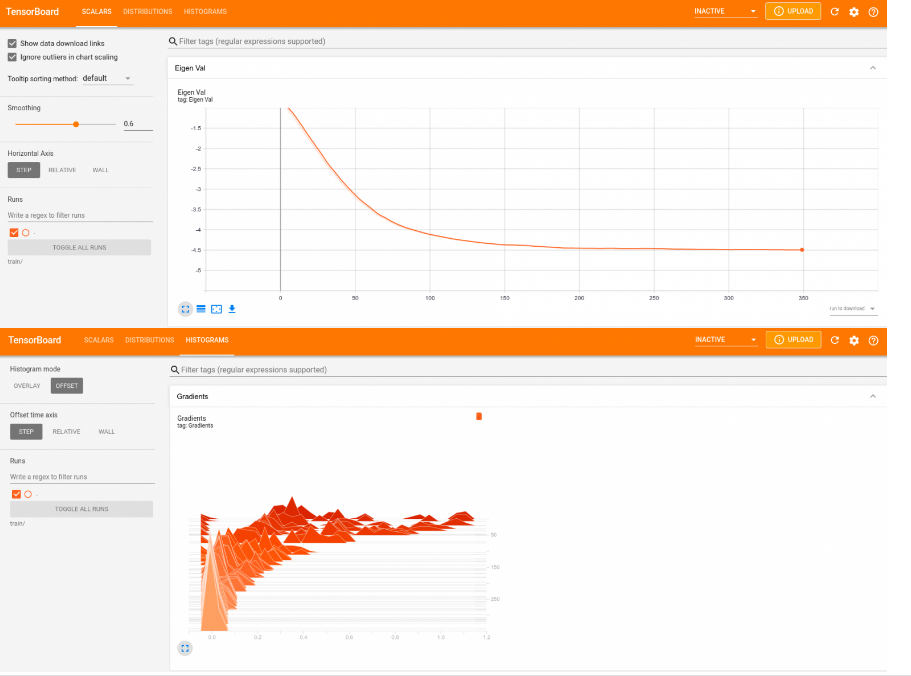
Conclusion:
Now very many private companies such as Google, IBM, Microsoft and others, as well as governments and institutions are spending huge resources on research in this direction. Quantum computers are already available today for testing in IBM and AWS cloud servers. Many scientists are expressing confidence in the imminent achievement of quantum superiority on practical tasks (let me remind you, superiority on a specially selected "convenient" for quantum computer task was achieved by Google last year). All this, plus the mystery and beauty of the quantum world, is what makes this field so attractive. I hope this article will help you immerse yourself in the marvellous quantum world too!