Diskussion zum Artikel "Statistische Verteilungen in MQL5 - Nur das Beste aus R" - Seite 19

[Aleksey Nikolayev]

Aleksey Nikolayev:
Es besteht der Wunsch, die Kolmogorov-Verteilung in die Bibliothek aufzunehmen. Sie ist sehr nützlich wegen ihrer Verwendung im Kolmogorov-Smirnov-Kriterium und im Problem der Suche nach der Zerlegung eines Zufallsprozesses.

Ich werde sie hier nur für den Fall der Fälle stehen lassen. Berechnung der CDF und ihrer Ergänzungen für die Verteilung der Kolmogorov-Smirnov-Statistik für den zweiseitigen Ein-Stichproben-Test.

[Aleksey Nikolayev]

Hat das jemand benutzt?

[Renat Fatkhullin]

Aleksey Nikolayev:

Die CDF der hypergeometrischen Verteilung wird von der Funktion MathCumulativeDistributionHypergeometric() falsch berechnet. Per Definition muss die Wahrscheinlichkeitsverteilungsfunktion für jede reelle Zahl definiert werden. Nachfolgend finden Sie ein Skript auf mql5 mit seinen Ergebnissen und zum Vergleich dasselbe auf R.

Ergebnis:

-1.0 nan 2

0.0 0.0 0

0,5 nan 2

Nullteilung in 'Hypergeometric.mqh' (241,35)

Ergebnis:

[1] 0.0000000 0.0000000 0.0000000 0.2222222

Sie haben falsche Argumente übergeben und ERR_ARGUMENTS_INVALID (2) erhalten. Wir überprüfen die Eingabeparameter genauer, und R scheint die Antwort durch Nullen ersetzt zu haben.

//+------------------------------------------------------------------+
//| Hypergeometrische kumulative Verteilungsfunktion (CDF) | |
//+------------------------------------------------------------------+
//| Die Funktion gibt die Wahrscheinlichkeit zurück, dass eine Beobachtung |
//| aus der Hypergeometrischen Verteilung mit den Parametern m,n,k |
//| ist kleiner oder gleich x.|
//||
//| Argumente:|
//| x : Die gewünschte Anzahl von Objekten |
//| m : Größe der Grundgesamtheit |
//| k : Anzahl der Artikel mit dem gewünschten Merkmal |
//|| in der Bevölkerung|
//| n : Anzahl der gezogenen Stichproben ||
//| tail : Flagge zur Berechnung des unteren Endes |
//| log_mode : Logarithmusmodus, bei true werden Log-Werte berechnet |
//| error_code : Variable für Fehlercode |
//||
//| Rückgabewert:|
//| Der Wert der hypergeometrischen kumulativen Verteilungsfunktion |
//| mit den Parametern m,n,k, ausgewertet bei x.
//+------------------------------------------------------------------+
//| Basierend auf dem Algorithmus von John Burkardt|
//+------------------------------------------------------------------+
double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code)
  {
//--- NaN prüfen
   if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- m,k,n,x muss ganzzahlig sein
   if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x))
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- m,k,n,x muss positiv sein
   if(m<0 || k<0 || n<0 || x<0)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- Prüfbereiche
   if(n>m || k>m)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

[Renat Fatkhullin]

Aleksey Nikolayev:

Einige (nicht alle) Binomialkoeffizienten sind z. B. negativ:

Ergebnis: -309196571788882235

sollte sein: 349615716557887488

Wegen des großen K (28) ist der 64-Bit-Long dort übergelaufen. Der Rückgabewert ist long.

Um Werte innerhalb solcher Grenzen zu zählen, müssen Sie die Funktion in Double-Werte umschreiben.

[Aleksey Nikolayev]

Renat Fatkhullin:

Sie haben falsche Argumente übergeben und ERR_ARGUMENTS_INVALID (2) erhalten. Wir überprüfen die Eingabeparameter genauer, und R scheint die Antwort durch Nullen ersetzt zu haben.

1) Jede CDF - Wahrscheinlichkeitsverteilungsfunktion (diskrete Funktionen sind keine Ausnahme!) MUSS unbedingt für alle reellen Zahlen definiert sein. Nachfolgend finden Sie ein Analogon des Codes in R mit seinem Ergebnis, das zeigt, wie dies in der Realität aussehen sollte. Übrigens zählen einige diskrete CDF-Funktionen korrekt und andere nicht.

2) Für den Wert 1 erhalten Sie einen Fehler bei der Division durch Null.

[Renat Fatkhullin]

Aleksey Nikolayev:

1) Jede CDF - Wahrscheinlichkeitsverteilungsfunktion (diskrete sind keine Ausnahme!) MUSS UNBEDINGT für alle reellen Zahlen definiert sein. Nachfolgend finden Sie ein Analogon des Codes in R mit seinem Ergebnis, das zeigt, wie dies in der Realität berücksichtigt werden sollte. Übrigens, einige diskrete CDF-Funktionen haben Sie richtig gezählt und andere nicht.

2) Für den Wert 1 erhalten Sie einen Fehler bei der Division durch Null.

Lesen Sie den Code der Funktion und ihre Überprüfung, er steht im Quellcode.

Ich habe R nicht zur Hand, ich muss es separat überprüfen. Ich sehe Division durch Null, wir müssen die Randbedingungen verstehen.

[Aleksey Nikolayev]

Renat Fatkhullin:

Wegen eines großen K (28) wurde der 64-Bit-Long dort überlaufen. Der Rückgabewert ist long.

Um Werte innerhalb solcher Grenzen zu zählen, sollten Sie die Funktion auf Double-Werte umschreiben.

Das ist klar. Es ist nur so, dass es einen Fehler mit dem Logarithmus des Binomialkoeffizienten bei ganzzahligen Argumenten gibt und ich dachte, dass dies der Grund sei. Jetzt habe ich mir den Code angesehen und festgestellt, dass ich mich geirrt habe - der Grund ist ein anderer.

#include <Math\Stat\Math.mqh>

void OnStart()
  { Print(MathBinomialCoefficientLog(62,28));
    Print(MathBinomialCoefficientLog(62.0,28.0));
  }

Ergebnis:

test_clog (EURUSD.m,MN1) -nan(ind)

test_clog (EURUSD.m,MN1) 40.39561099351077

PS Falsch, das Problem liegt auch im Überlauf

[Aleksey Nikolayev]

Renat Fatkhullin:

Es ist kein R vorhanden,

R online

[Denis Kirichenko]

Einige Probleme mit NoncentralBeta. Ich habe das Skript aus der Dokumentation übernommen.

Dies sind die Ergebnisse für verschiedene Parameter.

[Denis Kirichenko]

Formel in der Dokumentation:

Ist das Analogon in Wikipedia:

Ich habe mir den Code angesehen.

Die Funktion MathRandomNoncentralBeta() hat Zeilen wie diese:

//--- Zufallszahl mit Noncentral ChiSquare erzeugen
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code);
result[i]=chi1/(chi1+chi2);

In der gleichen Wikipedia steht dies:

The noncentral beta distribution (Type I) is the distribution of the ratio

wobei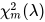 einenichtzentrale Chi-Quadrat-Zufallsvariable mit Freiheitsgraden m und dem Nicht-Zentralitätsparameter 𝜆 ist, und 𝜒 𝑛 2 eine zentrale chi-Quadrat-Zufallsvariable mit Freiheitsgraden n ist, die unabhängig von 𝜒 𝑚 2 ( 𝜆 ) ist.

Das heißt, es werden zwei Zufallsvariablen genommen, wobei die erste aus einer nicht zentralen chi-Quadrat-Verteilung und die zweite aus einer zentralen stammt. Wahrscheinlich kann der Code dahingehend korrigiert werden:

//--- Zufallszahl mit Noncentral ChiSquare erzeugen
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomChiSquare(b2,error_code);
result[i]=chi1/(chi1+chi2);

Die geänderten Graphen im Beispiel werden unten stehen.