Diskussion zum Artikel "Universelles Regressionsmodell für die Prognostizierung von Marktpreisen" - Seite 8
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Nehmen Sie über eine private Nachricht Kontakt auf und informieren Sie sich über die Bedingungen.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Werden die Indikatoren bezahlt oder so? Veröffentlicht in der Codebase, verwenden Sie es nach Herzenslust!
Neuer Artikel Universal Regression Model for Market Price Prediction ist veröffentlicht:
Autor: Юсуфходжа
guter Artikel.
sehr beeindruckend
Es ist schade, aber gleich zu Beginn des Artikels gibt es Fehler.
Erstens: Der Preisanstieg zu einem bestimmten Zeitpunkt t hat natürlich einen bestimmten Wert, den wir mit D0 bezeichnen. Nehmen wir an.
Weiter... Zum Zeitpunkt t=0 gibt es also keine Auswirkung auf den Preis, und offensichtlich gibt es auch keinen Preisanstieg durch die externe Auswirkung. Dennoch haben wir das Delta wieder D0 genannt.
Dann setzen wir dt/tau in die Formel ein, die ohnehin 1/C^2 ist, d.h. wir haben dem Einfluss eine Beschleunigung gegeben, die die geometrische Regression ohnehin verschieben wird. Warum sollten wir? Schließlich haben wir noch nicht definiert - was dieser Stoß so ist...
naja, ganz allgemein.
Es ist schade, aber gleich zu Beginn des Artikels gibt es Fehler.
Erstens hat der Preisanstieg zu einem bestimmten Zeitpunkt t natürlich einen bestimmten Wert, den wir mit D0 bezeichnen. Nehmen wir an.
Weiter... Zum Zeitpunkt t=0 gibt es also keine Auswirkung auf den Preis, und offensichtlich gibt es auch keinen Preisanstieg durch die externe Auswirkung. Dennoch haben wir das Delta wieder D0 genannt.
Dann setzen wir dt/tau in die Formel ein, die ohnehin 1/C^2 ist, d.h. wir haben dem Einfluss eine Beschleunigung gegeben, die die geometrische Regression ohnehin verschieben wird. Warum sollten wir? Wir haben doch noch gar nicht definiert - was dieser Stoß so ist...
Nun, ganz allgemein...
1. Do ist nicht der Preisanstieg, sondern das anfängliche Potenzial der Kraft, die zum Zeitpunkt t=0 auf den Preis wirkt.
2. aus dem Artikel: ".... nehmen wir an, dass sich der Marktpreis, der sich im Gleichgewicht befindet, nur unter der Einwirkung einer externen Kraft D(t) ändern kann, deren Größe und Wert wir in derselben Dimension wie den Preis messen werden.
Nehmen wir weiter an, dass die Veränderung des Marktpreises P(t) im Laufe der Zeit t seit Beginn des Einflusses dieser Kraft, die von Null an durch eine uns noch unbekannte Regelmäßigkeit kontinuierlich ansteigt, dazu neigt, im Unendlichen den Wert P(∞) = D0 zu erreichen. Das heißt, mit D0 meinen wir eine endliche Zunahme oder Abnahme des Marktpreises, je nach Art und Vorzeichen dieser Einflusskraft.
Außerdem nehmen wir an, dass D(t=0) = D0 ist. Nehmen wir weiter an, dass während der infinitesimalen Zeitspanne dt die Einflusskraft um den Wert dD(t) im Verhältnis zur verbleibenden Kraft D(t) zum Zeitpunkt t abnimmt:
Daraus ergibt sich die exponentielle Abhängigkeit von D(t) von der Zeit t in der Form:
Wobei: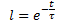
t - Zeit vom Beginn der Einwirkung der destabilisierenden Kraft in Zeitreiheneinheiten, sec. (min, Stunden, Tage, Wochen, Jahrzehnte, Monate, Jahre);
τ (tau) - der Proportionalitätskoeffizient, numerisch gleich der Zeitkonstante des Prozesses, sec.(min, Stunden, Tage, Wochen, Dekaden, Monate, Jahre)".
Woher haben Sie die Dimensionalität von 1/s^2? Dieses Verhältnis hat keine Dimensionalität. Ich habe es nicht hineingeschmuggelt, sondern die Hypothese aufgestellt, dass die Änderungsrate (Abnahme) einer Kraft, die auf einen Prozess wirkt, proportional zur Kraft selbst ist, was der Logik nicht widerspricht, und dann wurde diese Hypothese vollständig bestätigt. Als Proportionalitätskoeffizient führte er das Verhältnis a (alpha) = 1/tau ein, das den Kehrwert der Zeit, die Dimension, hat. Unter a (alpha) verstehe ich die Impedanz des Systems, d.h. den Widerstand des Systems gegen den Fluss des Prozesses, und tau ist das Bild der Zeit in der Laplace-Transformation, wie sich später herausstellte, und erlaubt es, die Analyse des Prozesses aus dem Differentialbereich in den gewöhnlichen Bereich zu übertragen. Das bedeutet, dass jeder Prozess seine eigene Zeit hat, die sich von der unseren unterscheidet, und tau fungiert als "Übersetzer" der Zeiten, wenn ich es so ausdrücken darf. In den Eingeweiden des Artikels habe ich eine Methode zur Schätzung von tau angegeben:
Wenn nun die Werte der Funktion f zu den entsprechenden Zeitpunkten t bekannt sind, dann werden aus dieser Gleichung die Parameter n, τ und der Koeffizient β wie folgt bestimmt:
wobei:
Die Werte der Funktion f zu den entsprechenden Zeitpunkten t und t werden durch die tatsächlichen Werte des Marktpreises P0, P1,..., Pk zu den Zeitpunkten h0, h1,..., һk ab dem Beginn seiner Destabilisierung durch numerische Differenzierung bestimmt, bezogen auf die Mitte des Intervalls:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); und so weiter;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; und so weiter.