3. Als Nächstes beschloss ich, die Anzahl der Balken in den Dreiecken auf 7 zu erhöhen, also habe ich das Skript ein wenig überarbeitet:
// Скрипт для подсчёта соотношения чисел затухающих и разгорающихся треугольников // // Skript OtnoshZatRazTreug, июнь 2012 // Примечание: скрипт может немного подвисать на ТФ M1. #property copyright "Copyright © Svinotavr-2000" #property link "DmitriyN" //#property show_inputs int start() { // Декларация double DliPer; // Длительность периода исследования, лет double n; // Количество бар, шт double KolZatTre; // Количество затухающих треугольников, шт double KolRazTre; // Количество разгорающихся треугольников, шт double OtnoshZatRaz; // Отношение числа затухающих треугольников к числу разгорающихся, раз double Pogreshnost; // Погрешность исследования, % // Берём число бар на 6 меньшее, чем всего n=Bars-6; // Цикл по всем барам for(int j = 0; j < n; j++) { // Считаем количество ЗАТУХАЮЩИХ треугольников =========== // Проверяем, являются ли High баров после начального бара (j+5) // _ меньше либо равными High начального бара (j+5) if (High[j+6] >= High[j+5]) { if (High[j+6] >= High[j+4]) { if (High[j+6] >= High[j+3]) { if (High[j+6] >= High[j+2]) { if (High[j+6] >= High[j+1]) { if (High[j+6] >= High[j]) { // Проверяем, являются ли Low баров после начального бара (j+5) // _ больше либо равными Low начального бара (j+5) if (Low[j+6] <= Low[j+5]) { if (Low[j+6] <= Low[j+4]) { if (Low[j+6] <= Low[j+3]) { if (Low[j+6] <= Low[j+2]) { if (Low[j+6] <= Low[j+1]) { if (Low[j+6] <= Low[j]) { KolZatTre=KolZatTre+1; }}}}}} }}}}}} // Считаем количество РАЗГОРАЮЩИХСЯ треугольников =========== // Проверяем, являются ли High баров после начального бара (j+5) // _ больше либо равными High начального бара (j+5) if (High[j+6] <= High[j+5]) { if (High[j+6] <= High[j+4]) { if (High[j+6] <= High[j+3]) { if (High[j+6] <= High[j+2]) { if (High[j+6] <= High[j+1]) { if (High[j+6] <= High[j]) { // Проверяем, являются ли Low баров после начального бара (j+5) // _ меньше либо равными Low начального бара (j+5) if (Low[j+6] >= Low[j+5]) { if (Low[j+6] >= Low[j+4]) { if (Low[j+6] >= Low[j+3]) { if (Low[j+6] >= Low[j+2]) { if (Low[j+6] >= Low[j+1]) { if (Low[j+6] >= Low[j]) { KolRazTre=KolRazTre+1; }}}}}} }}}}}} } // Вычисляем длительность периода истории исследования (календарный) DliPer = n*Period()/(1440*365); // Считаем отношение числа затухающих треугольников к разгорающимся OtnoshZatRaz=KolZatTre/KolRazTre; // Вычисляем погрешность расчётов Pogreshnost=(1/(KolZatTre) + 1/(KolRazTre))*100; // Формируем строки для печати string S0 = "\n" + "================= Результаты расчётов =================" + "\n" + "\n"; string S1 = "Исследовано бар = " + DoubleToStr(n,0)+ " шт" + "\n"; string S2 = "Длительность периода исследования = " + DoubleToStr(DliPer,1)+ " лет" + "\n"; string S3 = "Погрешность расчётов = " + DoubleToStr(Pogreshnost,3)+ " %"+ "\n"; string S4 = "Отношение числа затухающих треугольников к разгорающимся = " + DoubleToStr(OtnoshZatRaz,3)+ " раз"+ "\n"; string S5 = "Число затухающих треугольников = " + DoubleToStr(KolZatTre,0)+ " шт"+ "\n"; string S6 = "Число разгорающихся треугольников = " + DoubleToStr(KolRazTre,0)+ " шт"; // Выводим строки на экран Comment(S0, S1, S2, S3, S4, S5, S6); }
Ein Beispiel für das Ergebnis des Skripts:
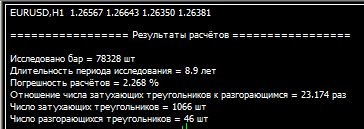
Sie werden mir zustimmen, dass die Differenz von 23,1 Mal bei einer Rechengenauigkeit von etwas über 2 % kaum als Regelmäßigkeit bezeichnet werden kann.
Welche Schlussfolgerung lässt sich aus all dem ziehen? Die Schlussfolgerung ist, dass der Preis eine Orientierung (Richtung) hat.
Es ist durchaus möglich, dass bei einer Kursumkehr die von vielen Expert Advisors erzielten Ergebnisse ganz anders ausfallen und höchstwahrscheinlich zu Gunsten der Händler ausfallen werden:
Wenn Sie interessiert sind - lesen, denken, experimentieren...
Wenn Sie dieses Muster in einem Diagramm mit zufälligen Inkrementen, die in der Normalverteilung liegen, überprüfen wollen - nur zu :)
Wenn jemand konstruktive Kritik (konstruktiv, nicht wahllos) oder Vorschläge hat - ich werde gerne zuhören.
des letzteren - höchstwahrscheinlich das, was Sie als verblassende Dreiecke und sogar auf der Uhr bezeichnen - ist nur eine saisonale Abnahme der Kerzenvolatilität :-)
und weiter, Sie haben sozusagen die Referenzpunkte gefunden - aber darüber hinaus - das Verhalten der Balken (Bewegungsrichtung) - wird ungefähr 50/50 sein... daher hat all dies keinen praktischen Wert :-) (ohne Rücksicht auf MM :-) IMHO.
Wenn jemand konstruktive Kritik (konstruktiv, nicht wahllos) oder Vorschläge hat, würde ich mich freuen, sie zu hören.
Wenn Sie auf der Suche nach Mustern im Forex sind, dann seien Sie anständig:
Wenn Sie nach einem Muster suchen, seien Sie anständig. 1. geben Sie die Daten eines Maklerunternehmens an oder vergleichen Sie die Daten verschiedener Maklerunternehmen, denn für mich sind die Muster von Filtern von geringem Interesse.
2) Geben Sie nicht nur ein Währungspaar und einen TF an, sondern besser - in der Tabelle wieder verschiedene Paare und verschiedene TFs.
Wenn wir einen solchen Tisch haben, können wir darüber reden...
;)
Die obigen Fehler wurden korrigiert.
| Zeitrahmen | Verhältnis, mal | Genauigkeit, % | Zeitraum der Geschichte, Jahre |
|---|---|---|---|
| М1 | 2,185 | 0,003 | 8,3 |
| М5 | 3,849 | 0,038 | 8,9 |
| М15 | 9,569 | 0,313 | 8,9 |
| М30 | 14,39 | 0,836 | 8,9 |
| Н1 | 23,17 | 2,268 | 8,9 |
Bei TF H4 wird der Fehler unannehmbar groß - nicht genügend Daten.
Die Anzahl der verblassenden Dreiecke beträgt 143, und die Anzahl der aufflackernden Dreiecke ist 1 (eins) pro Geschichte von 9 Jahren.
Höchstwahrscheinlich müssen die Methode zur Berechnung der Genauigkeit und der Algorithmus zur Formalisierung der Dreiecke überarbeitet werden.
Und wenn wir Ihr Skript noch etwas komplizierter machen, können wir die zeitliche Häufigkeit der Dreiecke überprüfen
zum Beispiel innerhalb eines Handelsmonats, einer Woche, eines Tages
Imho wäre der praktische Nutzen eher
Tabelle 2: Paar - GBPUSD | Demokonto| Alpari-Quotierungen | 7-Bar-Dreiecke
| Zeitrahmen | Verhältnis, mal | Genauigkeit, % | Zeitraum der Geschichte, Jahre |
|---|---|---|---|
| M1 | 2,844 | 0,004 | 8,1 |
| M5 | 4,289 | 0,041 | 8,8 |
| M15 | 7,688 | 0,243 | 8,9 |
| M30 | 10,84 | 0,642 | 8,9 |
| H1 | 17,25 | 1,793 | 8,9 |
Bei der TF H4 ist der Fehler groß - etwa 17,3 %. Die Anzahl der Dreiecke in der 9-Jahres-Geschichte beträgt 161 Stück / 6 Stück = 26,8 Mal.
Ich habe beschlossen, die Nachrichten in einen separaten Thread zu verschieben...
1. Alles begann damit, dass ich das Buch von Williams noch einmal las und beschloss, den Anteil der inneren Balken auf dem Diagramm zu überprüfen. Dann beschloss ich, den Anteil der inneren und äußeren Balken zu vergleichen, und stellte folgendes Muster fest: Der Anteil der inneren Balken ist höher als der Anteil der äußeren Balken.
Dies ist auch ohne jegliche Experimente offensichtlich.
Welche Pappeln sind eher "innen" oder "außen"? natürlich "innen"!
Denn die äußeren sind die großen, und die großen, langen Pappeln... ugh, Balken - offensichtlich weniger statistisch als die kleinen, kurzen Balken. Lange Kerzen sind weniger häufig. Kurze öfters.
Ein Muster? Ja.
Und nun die Frage: Und was bringt uns das?
die Antwort: ein Netz!
Anreicherungsrezept:
Wir nehmen eine kleine Stange in die sich verengende Kette, und legen das Netz zu beiden Seiten, mit einer Nachfüllung, je weiter - je mehr Nachfüllung. In wessen Richtung der erste im Gewinn spielen wird - er hat gewonnen.
2. Dieser Logik folgend, beschloss ich, das Verhältnis von inneren und äußeren Dreiecken zu untersuchen. Ich nannte die inneren Dreiecke gedämpft und die äußeren Dreiecke aufgeweitet.
Zu diesem Zweck wurde ein einfaches Skript geschrieben:
Es wäre auch gut, Statistiken über die Größe dieser Dreiecke an den einzelnen Punkten sowie über die Zeit (Tage) ihrer Bildung zu erstellen.
Ich gehe davon aus, dass die verblassenden Dreiecke in den Nachrichten auftreten.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Ich habe beschlossen, die Beiträge in einen separaten Thread zu verschieben...
1. Alles begann damit, dass ich das Buch von Williams erneut las und beschloss, den Anteil der inneren Balken im Diagramm zu überprüfen. Dann beschloss ich, den Anteil der inneren und äußeren Balken zu vergleichen, und stellte dabei folgendes Muster fest: Der Anteil der inneren Balken ist höher als der Anteil der äußeren Balken.
Ich möchte Sie daran erinnern, was innere und äußere Balken sind:
In der Abbildung oben: Takt B für Takt A ist extern und Takt F für Takt R ist intern.
Für die Forschung in diesem Bereich wurde ein einfaches Skript geschrieben:
Beispiel für das Ergebnis des Skripts:
2. Dieser Logik folgend beschloss ich, die Beziehung zwischen inneren und äußeren Dreiecken zu untersuchen. Ich nannte die inneren Dreiecke "fading" und die äußeren Dreiecke "flaring".
Zu diesem Zweck habe ich ein einfaches Skript geschrieben:
Das obige Skript analysierte Dreiecke mit einer Größe von sechs (6) Balken. In diesem Skript wurde eine sehr einfache Methode zur Berechnung des Berechnungsfehlers hinzugefügt.
Ein Beispiel für das Ergebnis des Skripts:
Ich möchte Sie daran erinnern, was verblassende und aufflackernde Dreiecke sind. Beispiel für ein verblassendes Dreieck (1) und ein aufflackerndes Dreieck (2):
1).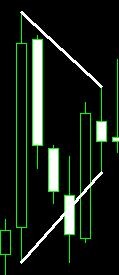 2).
2). 