我们的玛莎! - 页 2 123456789...21 新评论 Леонид 2009.01.19 14:31 #11 高水平的平滑化也不是一个好的结果--增加利润率。增加平滑度在任何情况下都会导致延迟的增加。但即使假设我们有零延迟，增加的平滑度将导致跳过较小的交易，这将减少交易量，并分别减少利润，从而增加缩水.....。 即使在图表上，你也可以清楚地看到，一部分相当大的交易，理论上可以采取，但没有采取，因此，利润已经下降.....。 [删除] 2009.01.19 14:44 #12 LeoV >> : 高水平的平滑化也不利于增加利润。增加平滑度在任何情况下都会导致延迟的增加。但是，即使我们假设我们有零延迟，增加的平滑度将导致跳过较小的交易，并因此导致交易的减少，分别导致利润的减少和提款的增加..... 适应性地调整到最佳变体。 >> 你描述的情况是所有时间相关指标的问题。摒弃古典意义上的时间，使用其他方法。 Леонид 2009.01.19 14:45 #13 mql4com писал(а)>> 放弃经典意义上的计时，使用其他方法。 我早就放弃了这样的TC，而使用其他的方法....，只是把这个帖子写成一个关于增加平稳性可以导致的意见)))))。 [删除] 2009.01.19 14:49 #14 LeoV писал(а)>> 我早就放弃了这样的TC，而使用其他的方法....，我只是写了一个帖子，作为对增加平稳性可能导致的意见)))))。 我可以给你写一封信吗？ Леонид 2009.01.19 15:19 #15 LeoV писал(а)>> 平滑度的增加将导致遗漏更多的小动作，从而导致交易数量的减少，分别是利润的减少，因此，提款的增加.....。 加上所有这些，你仍然需要加上增加延迟带来的误差（损失）（不需要利他主义），利润的问题可以悬在空中.....))))。 Swetten 写道(a)>> 我能给你写封信吗？)))当然，有可能....没有人取消个人.....)))) Neutron 2009.01.19 16:13 #16 MVV 写道（a） >>。 我愿意就这个想法的作者进行争论。最有可能的是，这个想法和MA一样古老。:)) 而且总的来说，这个主题对我来说很有趣--我自己也在从事这个工作。自然，不是所有的东西都像你的画中那样美丽。它显然缺乏大量的箭矢。 现在按顺序。 开盘/反转的信号在实践中应该是MA的拐点。等于零的导数将给出一个 "架子"，之后MA可能会向同一方向移动。 第1点的主要要求将始终与第2点相冲突。 为了使МА接近理想，它应该具有适应性。 在我看来，如果没有一个积极的MM，这样的系统不会带来利润。 好了，同志们!- 所以我们走的是正确的路。 该图显示了一个非常示意性的开/关位置的方法说明。 这个论点是值得商榷的（二阶导数与零相等），所以需要从你这边进行论证。至于极值（第一个导数等于零），似乎不需要论证。 对MA贴近报价的要求和同时对其平稳性的要求并不（也不能）冲突，而是相互补充。一个引人注目的例子是通常的指数平均EMA。它的递归形式正是从函数的最小化中得到的，它同时要求接近性和平稳性。 3.这可以被看作是方法的发展。首先，必须获得对函数形式的明显要求的解决方案。 斯韦滕 写道>> 请原谅，什么是FZ？ FZ - 相位延迟。来自DSP的一个术语。 TheXpert 19.01.2009 14:45 目标函数是基于对大纲的引用吗？ 不，我们仍然需要根据我提出的muv要求和你的修正来构建目标函数。 LeoV 写道(a)>> 太多的平滑不会给我们带来好的结果--它将增加利润。增加平滑度在任何情况下都会导致延迟的增加。但是，即使我们假设我们有零滞后，增加的平滑将导致跳过较小的交易，并因此导致交易的减少，分别导致利润的减少和缩减的增加.....。 无望... 我们可以改变平滑度，为此我们将有手柄（参数），我们可以转动这些手柄，看一看平衡曲线。找到最佳状态似乎可以解决你提出的两个问题。 TheXpert 2009.01.19 16:49 #17 Neutron >> :也许可以依次尝试一下？ 做一个最初的变体，分析它。 比如说喜欢这个，喜欢那个，不喜欢那个，那我们就把这个和那个拿掉，补上。 只是我看到有很多困惑，而最初的想法是很好的。 Neutron 2009.01.19 17:40 #18 TheXpert писал(а)>> 我们应该依次尝试吗？ 做一个初始版本，分析它。 比如喜欢这个，喜欢那个，不喜欢那个，所以我们就把这个和那个去掉，弄得一团糟。 只是我看到这里有很多困惑，原来的想法很好。 没有任何混乱! 如果没有别的事，让我们记住完美硕士的基本要求。 1.与原始VR的接近程度。这个要求等于商X （图片中的绿线）和平滑曲线 Y（蓝色）之间的距离小。可以这样写：平均而言，在一个大样本上，它必须满足。(X[i]-Y[i])^2-->min 2.MA的平稳性。这个要求等于平滑曲线的相邻样本之间的距离小：（Y[i]-Y[i-1]）^2-->min。 3.考虑到开放位置（图片中的垂直线之间）的方向（符号），将由从初始BP切下的碎片组成的权益曲线应该是增加的。仓位开放的符号等于MA导数的符号。在我们的术语中，符号（Y[i]-Y[i-1]）。 在这种情况下，股权曲线将由Kotier片组成，这些片子将根据要关闭的位置的符号对接在一起。这就是它的实施方式。让我们为科蒂尔构建一个第一差分序列（FDD）d[i]=X[i]-X[i-1]。，那么股权曲线的快速增长()，就相当于要求对它的第一次导数进行最大化。dE[i]/dt=E[i]-E[i-1]= 符号(Y[i]-Y[i-1])*(X[i]-X[ i-1])或用一个小的，但可以接受的，在我们的例子中，拉伸{(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max 显然，某个表达式的最大化等于符号相反的最小化。-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min. 就这样了。我们得到最小化所需的函数。 S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min 我们需要找到它相对于Y[i] 的最小值， 其中i 是 当前基准点。 Our Masha! 一个完全随机的过程和FOREX。 Big Expert Advisor example [删除] 2009.01.19 17:50 #19 很好，我们已经找到了这个解决方案，在一段时间内。下一步是什么？ TheXpert 2009.01.19 17:52 #20 Neutron >> : 不散！不散！不散 如果没有更多的愿望，让我们重温一下完美MA的基本要求。 IMHO，Y函数视图是缺失的。还是我错过了什么？ mql4com>>: 很好，在一段时间内找到了这样一个解决方案。然后呢？ 像什么？我们赚取 -- -- 利润率投资于目标功能。 123456789...21 新评论 您错过了交易机会： 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符（不带空格） 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号，请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置，否则您将无法登录。 忘记您的登录名/密码？ 使用 Google 登录
高水平的平滑化也不是一个好的结果--增加利润率。增加平滑度在任何情况下都会导致延迟的增加。但即使假设我们有零延迟，增加的平滑度将导致跳过较小的交易，这将减少交易量，并分别减少利润，从而增加缩水.....。
即使在图表上，你也可以清楚地看到，一部分相当大的交易，理论上可以采取，但没有采取，因此，利润已经下降.....。
高水平的平滑化也不利于增加利润。增加平滑度在任何情况下都会导致延迟的增加。但是，即使我们假设我们有零延迟，增加的平滑度将导致跳过较小的交易，并因此导致交易的减少，分别导致利润的减少和提款的增加.....
适应性地调整到最佳变体。
>> 你描述的情况是所有时间相关指标的问题。摒弃古典意义上的时间，使用其他方法。
我早就放弃了这样的TC，而使用其他的方法....，只是把这个帖子写成一个关于增加平稳性可以导致的意见)))))。
我早就放弃了这样的TC，而使用其他的方法....，我只是写了一个帖子，作为对增加平稳性可能导致的意见)))))。
我可以给你写一封信吗？
加上所有这些，你仍然需要加上增加延迟带来的误差（损失）（不需要利他主义），利润的问题可以悬在空中.....))))。
我愿意就这个想法的作者进行争论。最有可能的是，这个想法和MA一样古老。:))
而且总的来说，这个主题对我来说很有趣--我自己也在从事这个工作。自然，不是所有的东西都像你的画中那样美丽。它显然缺乏大量的箭矢。
现在按顺序。
在我看来，如果没有一个积极的MM，这样的系统不会带来利润。
好了，同志们!- 所以我们走的是正确的路。
该图显示了一个非常示意性的开/关位置的方法说明。
这个论点是值得商榷的（二阶导数与零相等），所以需要从你这边进行论证。至于极值（第一个导数等于零），似乎不需要论证。
对MA贴近报价的要求和同时对其平稳性的要求并不（也不能）冲突，而是相互补充。一个引人注目的例子是通常的指数平均EMA。它的递归形式正是从函数的最小化中得到的，它同时要求接近性和平稳性。
3.这可以被看作是方法的发展。首先，必须获得对函数形式的明显要求的解决方案。
斯韦滕 写道>>
请原谅，什么是FZ？
FZ - 相位延迟。来自DSP的一个术语。
TheXpert 19.01.2009 14:45
目标函数是基于对大纲的引用吗？
太多的平滑不会给我们带来好的结果--它将增加利润。增加平滑度在任何情况下都会导致延迟的增加。但是，即使我们假设我们有零滞后，增加的平滑将导致跳过较小的交易，并因此导致交易的减少，分别导致利润的减少和缩减的增加.....。
也许可以依次尝试一下？
做一个最初的变体，分析它。
比如说喜欢这个，喜欢那个，不喜欢那个，那我们就把这个和那个拿掉，补上。
只是我看到有很多困惑，而最初的想法是很好的。
我们应该依次尝试吗？
做一个初始版本，分析它。
比如喜欢这个，喜欢那个，不喜欢那个，所以我们就把这个和那个去掉，弄得一团糟。
只是我看到这里有很多困惑，原来的想法很好。
没有任何混乱!
如果没有别的事，让我们记住完美硕士的基本要求。
1.与原始VR的接近程度。这个要求等于商X （图片中的绿线）和平滑曲线 Y（蓝色）之间的距离小。可以这样写：平均而言，在一个大样本上，它必须满足。(X[i]-Y[i])^2-->min
2.MA的平稳性。这个要求等于平滑曲线的相邻样本之间的距离小：（Y[i]-Y[i-1]）^2-->min。
3.考虑到开放位置（图片中的垂直线之间）的方向（符号），将由从初始BP切下的碎片组成的权益曲线应该是增加的。仓位开放的符号等于MA导数的符号。在我们的术语中，符号（Y[i]-Y[i-1]）。 在这种情况下，股权曲线将由Kotier片组成，这些片子将根据要关闭的位置的符号对接在一起。这就是它的实施方式。让我们为科蒂尔构建一个第一差分序列（FDD）d[i]=X[i]-X[i-1]。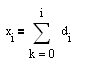
，那么股权曲线的快速增长(
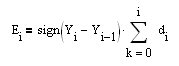)，就相当于要求对它的第一次导数进行最大化。dE[i]/dt=E[i]-E[i-1]= 符号(Y[i]-Y[i-1])*(X[i]-X[ i-1])或用一个小的，但可以接受的，在我们的例子中，拉伸{(Y[i]-Y[i-1])*(X[i]-X[i-1])}^2-->max 显然，某个表达式的最大化等于符号相反的最小化。-{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
就这样了。我们得到最小化所需的函数。
S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min
我们需要找到它相对于Y[i] 的最小值， 其中i 是 当前基准点。
不散！不散！不散
如果没有更多的愿望，让我们重温一下完美MA的基本要求。
IMHO，Y函数视图是缺失的。还是我错过了什么？
很好，在一段时间内找到了这样一个解决方案。然后呢？
像什么？我们赚取 -- -- 利润率投资于目标功能。