Импульс - страница 7

[Renat Akhtyamov]

Олег avtomat:
не понял... что на параболе?

как будет выглядеть это всё, если вместо функции воткнуть параболу?

[[Удален]]

добавим немножко быстрого квадратичного роста   (получим параболу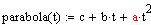     с наложенными колебаниями) 

[[Удален]]

new-rena:
как будет выглядеть это всё, если вместо функции воткнуть параболу?

ну так парабола - тоже функция.

[Vladimir Karputov]

Олег avtomat:

добавим немножко быстрого квадратичного роста

Интересные зависимости. А вот изменение цены на Форекс приблизительно можно описать каким уравнением из приведённых Вами?

[[Удален]]

Karputov Vladimir:
Интересные зависимости. А вот изменение цены на Форекс приблизительно можно описать каким уравнением из приведённых Вами?

я там уточнил, имея ввиду, что парабола

[Renat Akhtyamov]

Олег avtomat:

я там уточнил, имея ввиду, что парабола

понимаю. проще: s(t)=парабола, что получится?

[[Удален]]

new-rena:
понимаю. проще: s(t)=парабола, что получится?

Парабола - линия второго порядка. Её ускорение - постоянная величина, поэтому производная ускорения (рывок) равна нулю :

[Renat Akhtyamov]

Олег avtomat:

Парабола - линия второго порядка. Её ускорение - постоянная величина, поэтому производная ускорения (рывок) равна нулю :

а, ну да. т.е. возможно что при рывке=0 и есть начало/конец импульса?

[[Удален]]

Karputov Vladimir:
Интересные зависимости. А вот изменение цены на Форекс приблизительно можно описать каким уравнением из приведённых Вами?

Так ставить вопрос нельзя.    Если не накладывать каких-либо требований близости (по типу МНК и т.п), то такая постановка некорректна.

Ведь можно один и тот же участок движения цены описать и прямой линией, и синусоидой, и сложным набором различных составляющих. Всё будет зависеть от целей такого описания, а эти цели диктуют приемлемую степень близости аппроксимации к исходному ряду.

[[Удален]]

new-rena:
а, ну да. т.е. возможно что при рывке=0 и есть начало/конец импульса?

Реальное движение никогда не будет чистой параболой, даже если предположить отсутствие наложенных колебаний, поскольку всегда присутствуют шумы, которые болтают не только третью производную (т.е. рывок != 0 ), но и производные более высоких порядков.