Трейдинг: Предсказание финансовых временных рядов
Метод погружения позволяет количественно измерить предсказуемость реальных финансовых инструментов, т.е. проверить или опровергнуть гипотезу эффективности рынка. Согласно последней, разброс точек по всем координатам лагового пространства одинаков (если они - одинаково распределенные независимые случайные величины). Напротив, хаотическая динамика, обеспечивающая определенную предсказуемость, должна приводить к тому, что наблюдения будут группироваться вблизи некоторой гиперповерхности, т.е. экспериментальная выборка формирует некоторое множество размерности меньшей, чем размерность всего лагового пространства. Для измерения размерности можно воспользоваться следующим интуитивно понятным свойством: если множество имеет размерность D, то при разбиении его на все более мелкие покрытия кубиками со стороной d, число таких кубиков растет как d^-D. На этом факте основывается определение размерности W множеств уже знакомым нам методом box-counting. Размерность множества точек определяется по скорости возрастания числа ячеек (boxes), содержащих все точки множества.
Ниже приводится рисунок на котором изображена размерность (информационная) приращений этого ряда, подсчитанная методом box-counting для S&P500.
и утверждается, что в 15-мерном пространстве погружения экспериментальные точки формируют множество размерности примерно 4. Это значительно меньше, чем 15, что мы получили бы исходя из гипотезы эффективного рынка, считающей ряд приращений независимыми случайными величинами.
У меня возникло непонимание связанное с:
1.Получилось, что информационная размерность W равна числу входов D только для случая равномерного заполнения случайной величиной (СВ) всего фазового пространства. Уже, для СВ распределённой по гауссу(рассмотрим для примера двумерный случай), для D=1 - W=0. 7 т.е. ряд приращений в этом случае не является случайным, а это не так!
2. Для реализации способа, когда "размерность множества точек определяется по скорости возрастания числа ячеек (boxes), содержащих все точки множества", мы должны брать тем или иным способом n-кратый интеграл (сумму), где n заведомо больше 10-15. Это-же не реально по времени счёта!
Красивая статья, но в некоторых местах происходит подмена понятий (передергивание).
Для пояснения этого утверждения сошлюсь на самого автора. Фраза взята вот отсюда.
http://www.intuit.ru/department/expert/neurocomputing/2/4.html
«Многие представители разных наук, занимающихся перечисленными выше задачами и уже накопившими изрядный опыт их решения, видят в нейросетях лишь перепев уже известных им мотивов. Каждый полагает, что перевод его методов на новый язык нейросетевых схем ничего принципиально нового не дает. Статистики говорят, что нейросети - это всего лишь частный способ статистической обработки данных, специалисты по оптимизации - что методы обучения нейросетей давно известны в их области, теория аппроксимации функций рассматривает нейросети наряду с другими методами многомерной аппроксимации. Нам же представляется, что именно синтез различных методов и идей в едином нейросетевом подходе и является неоценимым достоинством нейрокомпьютинга. Нейрокомпьютинг предоставляет единую методологию решения очень широкого круга практически интересных задач. Это, как правило, ускоряет и удешевляет разработку приложений.»
Да ускоряет и удешевляет, но все ли сделанное быстро и дешево обладает хорошим качеством ? В этой статье говориться про предсказание финансового временного ряда. И всю жизнь предсказание (экстраполяция) означало ответ чему будет равно значение ряда, допустим через N минут (часов, дней) и точность прогноза всегда оценивалась величиной ошибки = качество.
И автор, зная, что НС не умеет экстраполировать, а только решает задачу интерполяции начинает передергивать, пытается подменить эти понятия. Поясню на примере. Всем хорошо известна программа FineRider распознает отсканированный текст (самый яркий пример использования НС). Но она - эта программа никогда не ответит на вопрос, что сделали с отсканированным листком. Т.е. НС применительно к финансовым рядам, может ответить в каком состоянии мы сейчас находимся, но не может предсказать, что будет дальше.
Методы предсказания (экстраполяции) и методы интерполяции очень схожи между собой, но цели у них разные.
Теперь вернемся к точности, автор плавно уходит и от этого вопроса, убеждая, что точность не важна, важен знак + или - и быстро переходит на Buy(Sell). C моей точки зрения, это грубейшая ошибка. Ну хорошо пусть будет + или -. А где ответ про время прогноза и сколько пунктов в плюс. Это что не важно? 1 пункт в плюс к концу года, или 100 пунктов к концу дня ?
Если правильно решить задачу экстраполяции, т.е. ответить на вопрос какой курс будет завтра в 12:00 с хорошей точностью, то принять решение о Buy(Sell) мы всегда сможем и думаю теория оптимального управления к примеру, принцип максимума Понтрягина, даст намного лучшую точку входа в рынок, чем начало торгового дня. Не надо сваливать все в одну кучу, адаптивное предсказание и принятие решений это разные по своей сути вещи.
И разводить тут наукообразие про возможность предсказания временного ряда не стоило. Нужно просто знать что такое корреляция, автор знает и говорит про то что именно это свойство лежит в основе предсказания, но видимо не знает, что для анализа предсказуемости временного ряда уже давно используют АКФ (автокорреляционную функцию). Надо просто 1 раз увидеть картинку и понять что такое АКФ. Участниками этого форума проведены исследования вида и параметров АКФ, и эти исследования говорят о том, что финансовый ряд предсказуем (и думаю не только нами). Кто хочет это проверить можете взять индикатор рассчитывающий АКФ вот отсюда ('Теория случайных потоков и FOREX'). И посмотреть, коррелирован ли этот процесс. Там все просто и наглядно, если дельта функция – то предсказать нельзя, т.к. нет корреляции.
В завершении хотел бы посоветовать тем, кто занимается НС (нейронными сетями), не наступать на грабли. Не делайте выходом НС Buy(Sell). Это дорога в никуда. Нельзя обучить на то чего нет (нет у этой кривой свойства Buy(Sell) это свойство принадлежит ТС ). Постарайтесь хотя бы делать как Better (выход это направление движения вверх или в низ). Попробуйте обучить на зиг-заг. Многие пытаются его (зигзаг) подать на вход, а может лучше это выход, то на что надо обучить НС.
...
2. Для реализации способа, когда "размерность множества точек определяется по скорости возрастания числа ячеек (boxes), содержащих все точки множества", мы должны брать тем или иным способом n-кратый интеграл (сумму), где n заведомо больше 10-15. Это-же не реально по времени счёта!
Но от глубины погружения зависит разрядность номеров боксов, а потому исследовать большую глубину при слишком малых d на MQL4 затруднительно.
Но от глубины погружения зависит разрядность номеров боксов, а потому исследовать большую глубину при слишком малых d на MQL4 затруднительно.
Непонятно:-)
Рассмотрим для примера случай одномерной СВ состоящей из N членов и как-то распределённых на заданном отрезке. Разобъём отрезок на N боксов (по числу членов СВ) и подсчитаем число попаданий в каждый бокс. Если решать задачу тупо - "в лоб", то нам придётся в каждом боксе (а их N) перебрать все элементы СВ (их тоже N). Таким образом, сложность задачи можно оценить как N^2. Для двумерной СВ, как-то распределённой на квадрате со стороной N, сложность, оценённая аналогичным образом, равна N^4 (N^2 боксов по N^2 членов СВ перебрать в каждом). Таким образом, для n-мерного ФП, сложность оценивается как N^2n, где n - можно рассматривать как глубину погружения.
Можно поступить хитрее, например, в каждой последующей ячейке, перебирать не все члены СВ, а только те, которые еще не встречались (действительно, одна и та же точка не может находится в двух местах одновременно). Тогда, для одномерного случая, в первом боксе мы переберём все элементы СВ - N штук, во втором на один меньше - N-1 и т.д. Сложность будет определятся как SUM(i), где i пробегает значения от 1 до N. В пределе, при N стремящимся в бесконечность, эта сумма стремится к величине 1/2*N^2. Для двумерной СВ, сложность оценённая аналогичным образом равна 1/2*N^4. Для n-мерного ФП, сложность оценивается как 1/2*N^2n, т.е. в два раза меньше, чем при решении путём тупого перебора.
Выигрыш в двойку.
Я не могу придумать способ, как ещё ускорить процесс. Да, разве это возможно? Ведь нам всёравно придётся по-очереди перебирать члены СВ в каждом боксе. Непонятно, как вы получили линейную сложность.
Но от глубины погружения зависит разрядность номеров боксов, а потому исследовать большую глубину при слишком малых d на MQL4 затруднительно.
Непонятно:-)
Рассмотрим для примера случай одномерной СВ состоящей из N членов и как-то распределённых на заданном отрезке. Разобъём отрезок на N боксов (по числу членов СВ) и подсчитаем число попаданий в каждый бокс. Если решать задачу тупо - "в лоб", то нам придётся в каждом боксе (а их N) перебрать все элементы СВ (их тоже N). Таким образом, сложность задачи можно оценить как N^2. Для двумерной СВ, как-то распределённой на квадрате со стороной N, сложность, оценённая аналогичным образом, равна N^4 (N^2 боксов по N^2 членов СВ перебрать в каждом). Таким образом, для n-мерного ФП, сложность оценивается как N^2n, где n - можно рассматривать как глубину погружения
...
Непонятно, как вы получили линейную сложность.
Для случая одномерной СВ имеем следующее:
- СВ ограничена отрезком ( длина отрезка r; минимальное значение
СВ m=min(X_i); r > max(X_i)-min(X_i) )
- Отрезок разбит на k боксов со стороной d (k=r/d, d подобрано соответственно,
что бы k было целым)
Тогда номер бокса для каждого элемента вычисляется так: N_i = [ (X_i - m)/d ], где
X_i - i-й член СВ,
N_i - номер бокса, которому принадлежит i-й член СВ,
[] - операция отбрасывания дробной части.
(Один пробег по всем членам СВ: сложность N, не зависит от k. Дополнительная память: N целых чисел.)
Далее задача сводится к подсчету количества использованных номеров боксов.
Для этого отсортируем массив номеров (quick sort, средняя сложность N*log(N)). Равные номера окажутся сгруппированными в последовательности.
По длине таких последовательностей мы можем, если надо, получить заселенность соответствующих боксов. А количество неравенств двух соседних элементов отсортированного массива дает нам количество задействованных боксов минус один.
(При подсчете количества задействованных боксов: один проход по отсортированному массиву N элементов.)
Таким образом, суммарная сложность: N + N*log(N) + N
Проще говоря, перебирать все возможные боксы нет необходимости, достаточно отмасштабировать и округлить исходные члены СВ до соответствующего бокса, после чего обработать результат округлений на предмет дубликатов значений.
В случае многомерной СВ процесс отличается только шагом перенумерации боксов.
Максимальный номер бокса при этом равен ((r/d)^n) - 1, где n - глубина погружения. Отмечу, что при малых d и больших n это значение может запросто стать больше максимального для int числа, а использовать арифметику с плавающей точностью нельзя, т.к. позже необходимо проверять на точное равенство.
Также при присвоении номера бокса члену СВ придется пробежаться по каждому измерению СВ и каждое, соответственно, отдельно отмасштабировать, округлить и скомбинировать в общий номер по принципу пересчета представления числа из k-й системы счисления.
Остальные шаги обрабатывают последовательность номеров боксов и, соответственно, в модификации не нуждаются.
Таким образом для многомерной СВ суммарная сложность: N*n + N*log(N) + N
...
Можно поступить хитрее, например, в каждой последующей ячейке, перебирать не все члены СВ, а только те, которые еще не встречались (действительно, одна и та же точка не может находится в двух местах одновременно). Тогда, для одномерного случая, в первом боксе мы переберём все элементы СВ - N штук, во втором на один меньше - N-1 и т.д. Сложность будет определятся как SUM(i), где i пробегает значения от 1 до N. В пределе, при N стремящимся в бесконечность, эта сумма стремится к величине 1/2*N^2. Для двумерной СВ, сложность оценённая аналогичным образом равна 1/2*N^4. Для n-мерного ФП, сложность оценивается как 1/2*N^2n, т.е. в два раза меньше, чем при решении путём тупого перебора.
Выигрыш в двойку.
Таким образом для многомерной СВ суммарная сложность: N*n + N*log(N) + N...
...принадлежность членов СВ боксам устанавливается за один проход по всем имеющимся членам СВ.
Теперь понятно!
E-e-h, спасибо огромное за предоставленный алгоритм. Действительно, всё получилось как Вы пишите.
но это теория. А на практике? Есть ли какието скрипты, программы?
Есть. Например, MathLab (с нейросетевым модулем) или deductor. А вообще-то полезно почитать Уоссермена "Нейрокомпьютерная техника - теория и практика" и написать свою сетку самому. =)
Эмпирические свидетельства предсказуемости финансовых рядов
Метод погружения позволяет количественно измерить предсказуемость
реальных финансовых инструментов, т.е. проверить или опровергнуть
гипотезу эффективного рынка. Согласно последней, разброс точек
по всем координатам лагового пространства одинаков (если они
- одинаково распределенные независимые случайные величины).
Напротив, хаотическая динамика, обеспечивающая определенную
предсказуемость, должна приводить к тому, что наблюдения будут
группироваться вблизи некоторой гиперповерхности 
, т.е. экспериментальная выборка формирует некоторое множество
размерности меньшей, чем размерность всего лагового пространства.
Для измерения размерности можно воспользоваться следующим
интуитивно понятным свойством: если множество имеет размерность
D, то при разбиении его на все более мелкие покрытия кубиками
со стороной 
, число таких кубиков растет как 
. На этом факте основывается определение размерности множеств
уже знакомым нам методом разбиения на квадраты (box-counting). Размерность
множества точек определяется по скорости возрастания числа
ячеек (boxes), содержащих все точки множества. Для ускорения алгоритма
размеры берут кратными 2, т.е. масштаб разрешения измеряется в битах.
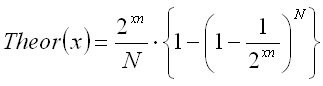, где N - число экспериментальных точек, n - размерность бокса (в
нашем примере n=1), x - ось абсцисс (в данном случае, число делений
отрезка по-полам).
Результат сравнения аналитического решения (синя сплошная линия) и данных, полученных прямым подсчётом числа заселённых боксов (сиреневые кружочки), показан на рис. ниже:
На нём, по оси абсцисс отложено отношение числа всех боксов (величина переменная) к числу экспериментальных точек, по оси ординат - отношение числа заполненных боксов (хотя бы одной точкой) к числу экспериментальных точек
Можно отметить хорошее совпадение модели и эксперимента. Но, что будет, если закон распределения СВ отличен от равномерного? Предположим, он нормален (гаусс), тогда заселённость будет себя вести иначе - красные кружочки. Для экспоненциального распределения СВ (что близко для финансовых рядов), получаем результат ещё более отличный от модели - чёрные кружочки. Заметим, что все три графика построены, для эффективной размерности (ЭР) n=1. Выходит, что для определения ЭР СВ нам нужно ещё априорное знание закона распределения приращений СВ по которому мы должны построить модель и затем сверять с ней полученные кривые заселённости. .. Как -то непросто получается. Ниже приведён рисунок, на котором показано как для равномерно распределённой СВ происходит заселение боксов в случае разной размерности ФП. Красными кружочками показана заселённость боксов для размерности ФП n=1, как функция от величины разбиения отрезка на котором она определена. Синими, для n=2. Чёрными - n=3. Оси определены, так же как и на предыдущем рис.
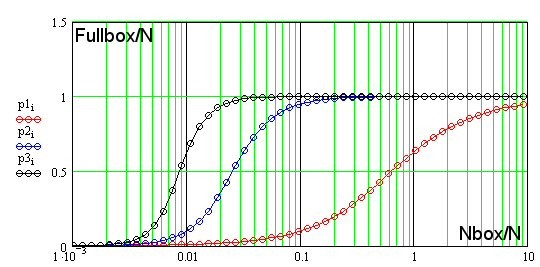
Очевидно, что для определения ЭР я должен сравнивать полученную кривую с модельным заселением, и только при их совпадении смогу определить искомую величину. Опять же, для построения модели, нужно знать распределение приращений. Как это автоматизировать? Не руками же подбирать константы?
В качестве примера типичного рыночного временного ряда возьмем такой известный финансовый инструмент, как индекс котировок акций 500 крупнейших компаний США (S&P500), отражающий среднюю динамику цен на Нью-Йоркской бирже. Рис. 3 показывает динамику индекса на протяжении 679 месяцев. Размерность (информационная) приращений этого ряда, подсчитанная методом box- counting, показана на рис. 4.
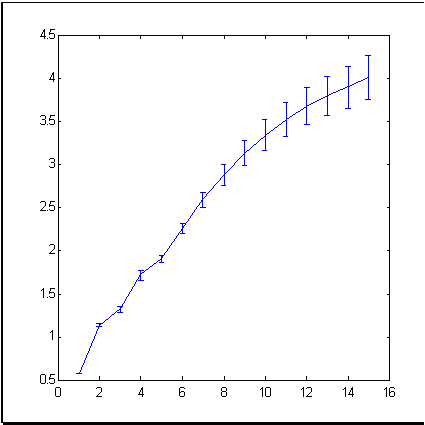
Рис. 4. Информационная размерность приращений ряда S&P500
Как следует из последнего рисунка, в 15-мерном пространстве погружения экспериментальные точки формируют множество размерности примерно 4. Это значительно меньше, чем 15, что мы получили бы исходя из гипотезы эффективного рынка, считающей ряд приращений независимыми случайными величинами.
Таким образом, эмпирические данные убедительно свидетельствуют о наличии некоторой предсказуемой составляющей в финансовых временных рядах, хотя здесь и нельзя говорить о полностью детерминированной хаотической динамике. Значит, попытки применения нейросетевого анализа для предсказания рынков имеют под собой веские основания.
Что ж, возмём и мы в качестве примера типичного рыночного временного ряда такой известный финансовый инструмент, как индекс котировок акций 500 крупнейших компаний США (S&P500, ТФ=1 месяц) за 2004-2005 гг. Смоделируем случайный временной ряд имеющий такоеже распределение приращений как и ряд приращений S&P500. Теперь сравним динамику заселения боксов модельным рядом (синяя линия) и рядом S&P500 (красные точки), для размерности фазового пространства (ФП) n=1 рис. слева.
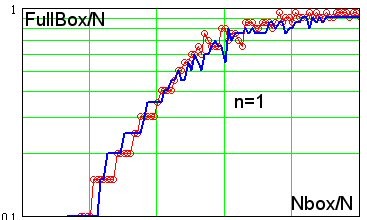
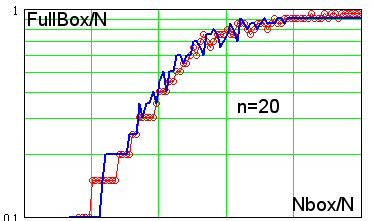
Можно отметить хорошее совпадение их скоростей заселения, что говорит об отсутствии скрытых закономерностей в ряде приращений S&P500 по крайней мере для размерности ФП равной 1. Однако то же хороше совпадение наблюдается и для n=2, и для 3,4...10...15, даже для n=20 - скорость заселения боксов ряда S&P500 не отличается от ряда полученного интегрированием случайной величины, см. рис. справа.
Позволю себе перефразировать автора:
Как следует из последнего рисунка, в 20-мерном пространстве погружения экспериментальные точки формируют множество размерности примерно 20. Это столько же, сколько мы получили исходя из гипотезы эффективного рынка, считающей ряд приращений независимыми случайными величинами.
Таким образом, эмпирические данные (если я нигде не ошибся) убедительно свидетельствуют об отсутствии некоторой предсказуемой составляющей в финансовых временных рядах. Значит, попытки применения нейросетевого анализа для предсказания рынков могут и не иметь под собой веских оснований.
Хорошо бы услышать коментарий автора статьи.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
New article Предсказание финансовых временных рядов has been published:
Предсказание финансовых временных рядов - необходимый элемент любой инвестиционной деятельности. Сама идея инвестиций - вложения денег сейчас с целью получения дохода в будущем - основывается на идее прогнозирования будущего. Соответственно, предсказание финансовых временных рядов лежит в основе деятельности всей индустрии инвестиций - всех бирж и небиржевых систем торговли ценными бумагами.
В данной статье рассмотрено одно из самых популярных практических приложений нейросетей - предсказание рыночных временных рядов. В этой области предсказания наиболее тесно связаны с доходностью и могут рассматриваться как один из видов бизнеса.
Предсказание финансовых временных рядов - необходимый элемент любой инвестиционной деятельности. Сама идея инвестиций - вложения денег сейчас с целью получения дохода в будущем - основывается на идее прогнозирования будущего. Соответственно, предсказание финансовых временных рядов лежит в основе деятельности всей индустрии инвестиций - всех бирж и небиржевых систем торговли ценными бумагами.
Приведем несколько цифр, иллюстрирующих масштаб этой индустрии предсказаний (Шарп, 1997). Дневной оборот рынка акций только в США превышает 10 млрд долл. Депозитарий DTC (Depositary Trust Company) в США, где зарегистрировано ценных бумаг на сумму 11 трлн долл. (из общего объема 18 трлн долл.), регистрирует в день сделок примерно на 250 млрд долларов. Еще более активно идет торговля на мировом валютном рынке FOREX. Его дневной оборот превышает 1000 млрд долл. Это примерно 1/50 всего совокупного капитала человечества.
Известно, что 99% всех сделок - спекулятивные, т.е. направлены не на обслуживание реального товарооборота, а заключены с целью извлечения прибыли по схеме "купил дешевле - продал дороже ". Все они основаны на предсказаниях изменения курса участниками сделки. Причем, что немаловажно, предсказания участников каждой сделки противоположны друг другу. Так что объем спекулятивных операций характеризует степень различий в предсказаниях участников рынка, т.е. реально - степень непредсказуемости финансовых временных рядов.
Это важнейшее свойство рыночных временных рядов легло в основу теории "эффективного " рынка, изложенной в диссертации Луи де Башелье (L. Bachelier) в 1900 г. Согласно этой доктрине, инвестор может надеяться лишь на среднюю доходность рынка, оцениваемую с помощью индексов, таких как Dow Jones или S&P500 (для Нью-Йоркской биржи). Всякий же спекулятивный доход носит случайный характер и подобен азартной игре на деньги. В основе непредсказуемости рыночных кривых лежит та же причина, по которой деньги редко валяются на земле в людных местах: слишком много желающих их поднять.
Теория эффективного рынка не разделяется, вполне естественно, самими участниками рынка (которые как раз и заняты поиском "упавших" денег). Большинство из них уверено, что рыночные временные ряды, несмотря на кажущуюся стохастичность, полны скрытых закономерностей, т.е. хотя бы отчасти предсказуемы. Такие скрытые эмпирические закономерности пытался выявить в 30-е годы в серии своих статей основатель технического анализа Ральф Эллиот (R. Elliott).
В 80-е годы неожиданную поддержку эта точка зрения нашла в незадолго до этого появившейся теории динамического хаоса. Эта теория построена на противопоставлении хаотичности и стохастичности (случайности). Хаотические ряды только выглядят случайными, но, как детерминированный динамический процесс, вполне допускают краткосрочное прогнозирование. Область возможных предсказаний ограничена по времени горизонтом прогнозирования, но этого может оказаться достаточно для получения реального дохода от предсказаний (Chorafas, 1994). И тот, кто обладает лучшими математическими методами извлечения закономерностей из зашумленных хаотических рядов, может надеяться на большую норму прибыли - за счет своих менее оснащенных собратьев.
В этой статье мы приведем конкретные факты, подтверждающие частичную предсказуемость финансовых временных рядов, и даже оценим эту предсказуемость численно.
Author: MetaQuotes Software Corp.