Поэкспериментировал с BayesianOptimization.
У вас самый большой набор состоял из 9 оптимизируемых параметров. И вы говорили что долго считает
Попробовал набор из 20 параметров оптимизировать при 10 первых случайных наборах. Считал 1,5 часа - это только расчет самих комбинаций в BayesianOptimization, без учета времени расчета самой НС (я НС заменил на простенькую мат. формулу для эксперимента).
А если захочется 50 или 100 параметров пооптимизировать, то она наверное и 1 набор будет сутками вычислять. Думаю быстрее нагенерить десятки случайных комбинаций и посчитать их в НС.И потом отобрать лучшие по Accuracy.
В обсуждении пакета об этой проблеме говорится. Год назад автор написал, что если найдет более быстрый пакет для расчетов - то применит его, но пока - как есть. Там дали пару ссылок на др. пакеты с бейесовской оптимизацией, но совсем не понятно как их применить, для аналогичной задачи, в примерах др. задачи решаются.
bigGp - не находит набор данных SN2011fe для примера (видимо он с инета качался, а страница не доступна). Попробовать пример не получилось. Да и по описанию - какие-то дополнительные матрицы требуются.
laGP - какая-то запутанная формула в фитнес функции, и делает сотни ее вызовов, а сотни расчетов НС делать неприемлемо по времени.
kofnGA - может искать только Х лучших из N. Например 10 из 100. Т.е. это не оптимизация набора из всех 100.
Генетические алгоритмы тоже не подойдут, т.к. они тоже генерят сотни вызовов фитнес функции (расчетов НС).
В общем аналога нет, а сам BayesianOptimization слишком долгий.
Поэкспериментировал с BayesianOptimization.
У вас самый большой набор состоял из 9 оптимизируемых параметров. И вы говорили что долго считает
Попробовал набор из 20 параметров оптимизировать при 10 первых случайных наборах. Считал 1,5 часа - это только расчет самих комбинаций в BayesianOptimization, без учета времени расчета самой НС (я НС заменил на простенькую мат. формулу для эксперимента).
А если захочется 50 или 100 параметров пооптимизировать, то она наверное и 1 набор будет сутками вычислять. Думаю быстрее нагенерить десятки случайных комбинаций и посчитать их в НС.И потом отобрать лучшие по Accuracy.
В обсуждении пакета об этой проблеме говорится. Год назад автор написал, что если найдет более быстрый пакет для расчетов - то применит его, но пока - как есть. Там дали пару ссылок на др. пакеты с бейесовской оптимизацией, но совсем не понятно как их применить, для аналогичной задачи, в примерах др. задачи решаются.
bigGp - не находит набор данных SN2011fe для примера (видимо он с инета качался, а страница не доступна). Попробовать пример не получилось. Да и по описанию - какие-то дополнительные матрицы требуются.
laGP - какая-то запутанная формула в фитнес функции, и делает сотни ее вызовов, а сотни расчетов НС делать неприемлемо по времени.
kofnGA - может искать только Х лучших из N. Например 10 из 100. Т.е. это не оптимизация набора из всех 100.
Генетические алгоритмы тоже не подойдут, т.к. они тоже генерят сотни вызовов фитнес функции (расчетов НС).
В общем аналога нет, а сам BayesianOptimization слишком долгий.
Есть такая проблема. Связана с тем, что написан пакет вроде на чистом R. Но плюсы в его применении лично для меня перевешивают затраты время. Есть пакет hyperopt (Python)/ Не дошли руки попробовать, да и староват он.
Но думаю кто то все же перепишет Рпакет на С++. Можно конечно самому поковырять, перевести часть вычислений на GPU , но это море времени потребует. Только если сильно припрет.
Пока буду пользовать то что есть.
Удачи
Еще поэкспериментировал с примерами из самого пакета GPfit.
Вот пример оптимизации 1 параметра, который описывает кривую с 2 вершинами (ф-я из GPfit имеет больше вершин, я оставил 2):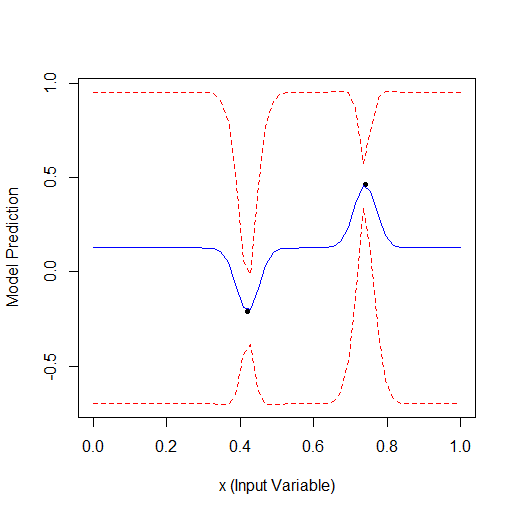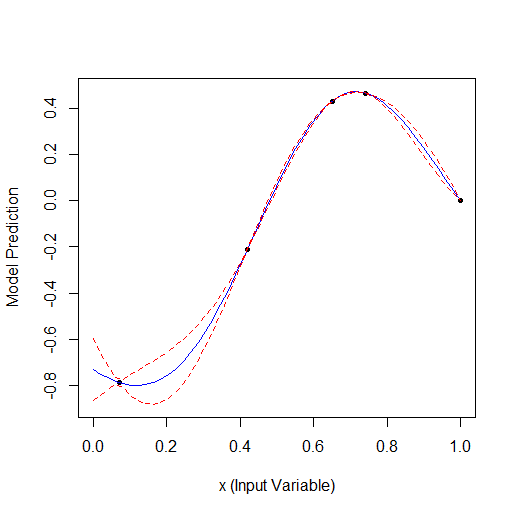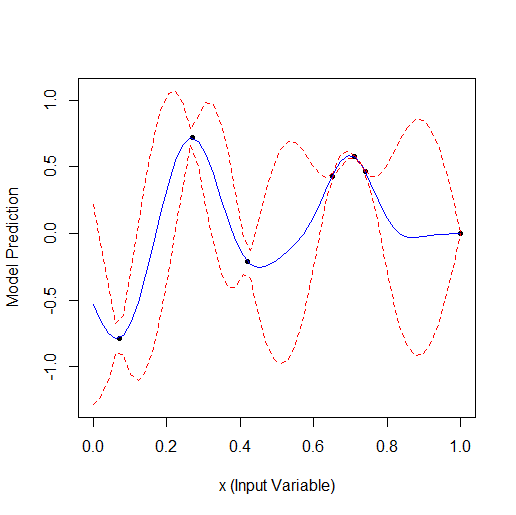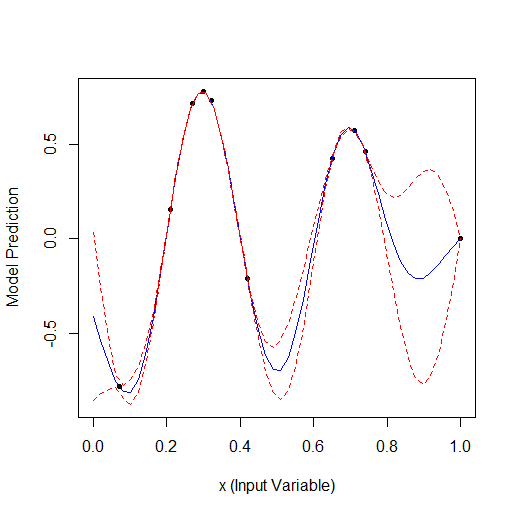
Взято 2 случайных точки, а потом оптимизация. Видно, что сначала находит малую вершину, а потом большую. Всего 9 расчетов - 2 случайных и + 7 по оптимизации.
Другой пример в 2D - оптимизирую 2 параметра. Оригинальная ф-я выглядит так: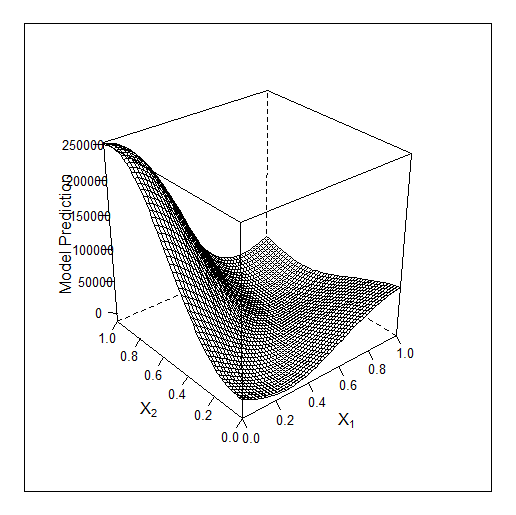
Оптимизация до 19 точек:

Всего 2 случайных точки + 17 найденных оптимизатором.
Сравнив эти 2 примера видно, что количество итераций нужных для нахождения максимума при добавлении 1 параметра удваивается. Для 1 параметра максимум нашелся за 9 расчитанных точек, для 2 параметров за 19.
Т.е. если оптимизировать 10 параметров, то может понадобиться 9 * 2^10 = 9000 вычислений.
Хотя на 14-точке алгоритм почти нашел максимум, это примерно в 1.5 раза увеличилось число расчетов. тогда 9* 1,5:10 = 518 вычислений. Тоже многовато, для приемлемого времени расчетов.
Результаты полученные в статье на 20 - 30 точках, могут оказаться далеки от реального максимума.
Думаю, что генетическим алгоритмам даже с этими простыми примерами понадобится намного больше точек просчитать. Так что лучшего варианта видимо все же нет.
Еще поэкспериментировал с примерами из самого пакета GPfit.
Вот пример оптимизации 1 параметра, который описывает кривую с 2 вершинами (ф-я из GPfit имеет больше вершин, я оставил 2):
Взято 2 случайных точки, а потом оптимизация. Видно, что сначала находит малую вершину, а потом большую. Всего 9 расчетов - 2 случайных и + 7 по оптимизации.
Другой пример в 2D - оптимизирую 2 параметра. Оригинальная ф-я выглядит так:
Оптимизация до 19 точек:
Всего 2 случайных точки + 17 найденных оптимизатором.
Сравнив эти 2 примера видно, что количество итераций нужных для нахождения максимума при добавлении 1 параметра удваивается. Для 1 параметра максимум нашелся за 9 расчитанных точек, для 2 параметров за 19.
Т.е. если оптимизировать 10 параметров, то может понадобиться 9 * 2^10 = 9000 вычислений.
Хотя на 14-точке алгоритм почти нашел максимум, это примерно в 1.5 раза увеличилось число расчетов. тогда 9* 1,5:10 = 518 вычислений. Тоже многовато, для приемлемого времени расчетов.
1. Результаты полученные в статье на 20 - 30 точках, могут оказаться далеки от реального максимума.
Думаю, что генетическим алгоритмам даже с этими простыми примерами понадобится намного больше точек просчитать. Так что лучшего варианта видимо все же нет.
Браво.
Наглядно.
На Ютубе размещен ряд лекций поясняющих как работает Байесовская оптимизация. Если не смотрели, советую посмотреть. Очень познавательно.
Как вставляли анимацию?
Стараюсь в последнее время использовать везде где возможно байесовские методы. Результаты очень хорошие.
1. Я делаю последовательную оптимизацию. Первая - инициализация 10 случайных точек, Вычисление 10-20 точек, последующие - инициализация 10 лучших результатов с предыдущей оптимизации, вычисления 10-20 точек. Как правило после второй итерации результаты не улучшаются значимо.
Удачи
На Ютубе размещен ряд лекций поясняющих как работает Байесовская оптимизация. Если не смотрели, советую посмотреть. Очень познавательно.
Я посмотрел код и результат в виде картинок (и вам показал). Самое важное это Gaussian Process из GPfit. А оптимизация - самая обычная - просто используется оптимизатор из стандартной поставки R и ищет максимум по кривой/фигуре которую придумала GPfit по 2м, 3м и т.д. точкам. А то, что она придумала - видно на анимированных картинках выше. Оптимизатор просто пытается выбраться наверх со 100 случайных точек.
Лекции может в будущем посмотрю, как время будет, а пока буду просто пользоваться GPfit как черным ящиком.
Как вставляли анимацию?
Просто пошагово отображал результат GPfit::plot.GP(GP, surf_check = TRUE) вставлял в фотошоп и там сохранил, как анимированный GIF.
последующие - инициализация 10 лучших результатов с предыдущей оптимизации, вычисления 10-20 точек.
По моим экспериментам - лучше все известные точки оставлять для будущих расчетов, т.к. если нижние удалить, то GPfit может подумать, что там есть интересные точки и захочет их просчитать, т.е. будут повторные запуски расчета НС. А с этими нижними точками GPfit будет знать, что в этих нижних областях искать нечего.
Хотя если результаты сильно не улучшаются, значит имеется обширное плато с небольшими колебаниями.
Как установить и запустить ?
).

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
Форвардное тестирование моделей с оптимальными параметрами
Проверим, как долго оптимальные параметры DNN будут выдавать результаты с приемлемым качеством для тестов "будущих" значений котировок. Тестирование будет проводиться в среде, оставшейся после предыдущих оптимизаций и тестирования, следующим образом.
Используем скользящее окно из 1350 баров, train = 1000, test = 350 (для валидации - первые 250 образцов, для тестирования - последние 100 образцов) с шагом 100, чтобы пройтись по данным после первых (4000 + 100) баров, использованных для предтренинга. Сделайте 10 шагов "вперед". На каждом шаге будут обучаться и тестироваться две модели:
- первая - с использованием предварительно обученной DNN, т.е. на каждом шаге выполнять тонкую настройку на новом диапазоне;
- вторая - дополнительное обучение DNN.opt, полученной после оптимизации на этапе тонкой настройки, на новом диапазоне.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Выполните первую часть форвард-теста, используя предварительно обученную DNN и оптимальные гиперпараметры, полученные в результате обучения варианта SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
Второй этап форвард-теста с использованиемDnn.opt, полученного в ходе оптимизации:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Сравните результаты тестирования, поместив их в таблицу:
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Точность Precision Recall F1 | Точность Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
Из таблицы видно, что первые два шага дают хорошие результаты. Качество на первых двух шагах обоих вариантов фактически одинаково, а затем падает. Поэтому можно предположить, что после оптимизации и тестирования ДНН будет поддерживать качество классификации на уровне тестового набора как минимум на 200-250 следующих полосах.
Существует множество других комбинаций для дополнительного обучения моделей на форвардных тестах, упомянутых в предыдущейстатье, и множество настраиваемых гиперпараметров.
Привет, в чем вопрос?
Здравствуйте Владимир,
не совсем понимаю, почему у вас НС тренируется на обучающих данных, а ее оценка делается на тестовых (если не ошибаюсь вы его используете как валидационный).
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
Не получится ли в этом случае подгонка под тестовый участок, т.е. будет выбрана модель, которая именно на тестовом участке лучше всего отработала?
Еще надо учесть, что тестовый участок достаточно мал и можно подогнаться под одну из временных закономерностей, которая может перестать работать очень быстро.
Может быть лучше делать оценку на обучающем участке, или на сумме участков, или как в Darch, (при поданных валидационных данных) на Err = (ErrLeran * 0.37 + ErrValid * 0.63) - эти коэффициенты по умолчанию, но их можно менять.
Вариантов много и неясно, какой из них лучше. Интересны ваши аргументы в пользу тестового участка.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Глубокие нейросети (Часть V). Байесовская оптимизация гиперпараметров DNN:
В статье рассматриваются возможности байесовской оптимизации гиперпараметров глубоких нейросетей, полученных различными вариантами обучения. Сравнивается качество классификации DNN с оптимальными гиперпараметрами при различных вариантах обучения. Форвард-тестами проверена глубина эффективности оптимальных гиперпараметров DNN. Определены возможные направления улучшения качества классификации.
Автор: Vladimir Perervenko