Conselhos práticos, por favor.

[Excluído] 2020.06.06 15:18

Pergunta: Como posso avaliar os resultados corretamente?

O erro de cada módulo é dado como uma porcentagem. 0% é o resultado ideal.

________________ PARÂMETROS ________________	Mod 1	Mod 2	Mod 3	Modo 4	Modo 5	(vi) Modo 6	(vi) Modo 7	(vi) Modo 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modo 15	Erro médio	Das tentativas
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Eu gostaria que o erro de cada módulo fosse mínimo, mas também gostaria que a dispersão fosse mínima.

Alexandr Andreev 2020.06.06 15:50 #1

Сергей Таболин:

Pergunta: Como posso avaliar os resultados corretamente?

O erro de cada módulo é dado como uma porcentagem. 0% é o resultado ideal.

________________ PARÂMETROS ________________	Mod 1	Mod 2	Mod 3	Modo 4	Modo 5	(vi) Modo 6	(vi) Modo 7	(vi) Modo 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modo 15	Erro médio	Das tentativas
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Eu quero que o erro de cada módulo seja mínimo, mas também quero que a propagação seja mínima.

produto de logaritmos

ZS: não tenho certeza do que é necessário, mas o logaritmo permitirá que os erros sejam tratados progressivamente, dará melhores resultados em casos individuais (módulos individuais). E a multiplicação é uma tentativa de reduzir a dispersão

Qualquer pergunta de novato, Comércio Forex Erros, bugs, perguntas

[Excluído] 2020.06.06 16:05 #2

Alexandr Andreev:

produto de logaritmos

ZS: Eu realmente não entendo o que é exatamente necessário, mas o logaritmo permitirá que os erros sejam tratados progressivamente, ele dará melhores resultados em casos individuais (módulos individuais). E a multiplicação é uma tentativa de reduzir a propagação

Obrigado. Epraticamente como é isso?

Alexandr Andreev 2020.06.06 16:22 #3

Сергей Таболин:

Obrigado. Epraticamente como é isso?

Provavelmente apenas o produto de

Opção1 ) Traduzir cada módulo para o estilo (1-x%) e multiplicá-los..... a resposta também é subtraída da unidade.

x% é o valor da célula

Opção2

Com logaritmos simplesmente pegamos o valor de uma célula e contamos logaritmo dela)))) o valor mais próximo de zero é a avaliação progressiva, ou seja, com alguma configuração de base 0,1 é melhor que 0,01 e também 0,1 é melhor que 1. Haverá apenas um parâmetro básico para o logaritmo com o qual vale a pena brincar.

FR H-Volatilidade O que é mais [Arquivo!] Qualquer pergunta de

[Excluído] 2020.06.06 18:51 #4

Alexandr Andreev:

Talvez um produto simples sirva.

Opção1 ) Traduzir cada módulo para o estilo (1-x%) e multiplicá-los..... A resposta também é subtraída da unidade.

x% é o valor da célula

Opção2

Com logaritmos simplesmente pegamos o valor de uma célula e contamos logaritmo dela)))) o valor mais próximo a zero é a avaliação progressiva, ou seja, com alguma configuração de base 0,1 é melhor que 0,01 e também 0,1 é melhor que 1. Haverá apenas um parâmetro básico do logaritmo com o qual vale a pena brincar.

Opção 1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

O que isso me diz?

Opção 2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

Este é o logaritmo com base 0,1

O que devo fazer com ele?

Eu tentei outras funções. Somente como eu os entendo também? ....

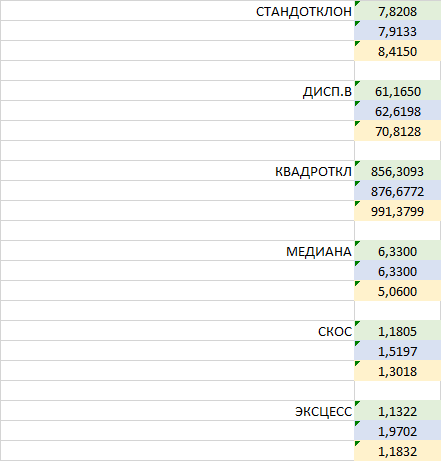
STANDOTCLONE	7,8208
	7,9133
	8,4150

DISP.B	61,1650
	62,6198
	70,8128

QUADROTKL	856,3093
	876,6772
	991,3799

MEDIANA	6,3300
	6,3300
	5,0600

SCOS	1,1805
	1,5197
	1,3018

EXCESS	1,1322
	1,9702
	1,1832

Practical advice, please. Circular Buffer Issue MQL5 Scoreboard

Dmitry Fedoseev 2020.06.06 18:58 #5

Encontre o máximo em cada linha, depois selecione a linha com o mínimo máximo. Perdoe o trocadilho))

[Excluído] 2020.06.06 19:12 #6

Dmitry Fedoseev:
Encontre o máximo em cada fileira, depois escolha a fileira com o mínimo máximo. Perdoe o trocadilho))

Máximo máximo na linha 3, mínimo máximo na linha 1. И? )))

Dmitry Fedoseev 2020.06.06 19:18 #7

Сергей Таболин:

Máximo máximo na linha 3, mínimo máximo na linha 1. И? )))

Escolha a primeira linha.

Alexandr Andreev 2020.06.06 21:15 #8

Сергей Таболин:

Opção 1

-3,43	-16,09	-14,82	-1,53	0,37	-16,72	-27,48	-4,70	-12,29	-4,70	-7,23	-5,33	0,37	-2,16	-5,96	10601305851,38
-4,06	-16,72	-11,66	-2,80	0,37	-18,62	-28,11	-3,43	-8,49	-4,06	-5,33	-5,33	-0,90	-0,90	-5,33	-6223799946,09
-3,43	-19,25	-15,46	-3,43	0,37	-16,72	-28,75	-5,33	-4,06	-7,23	-9,13	-4,06	0,37	-0,27	-3,43	1237520122,21

O que isso me diz?

Opção 2

-0,64640373	-1,23274206	-1,19920648	-0,40312052	0,200659451	-1,24846372	-1,45453998	-0,75587486	-1,12352498	-0,75587486	-0,91539984	-0,80140371	0,200659451	-0,49968708	-0,84260924
-0,70415052	-1,24846372	-1,10243371	-0,5797836	0,200659451	-1,292699	-1,46404221	-0,64640373	-0,97726621	-0,70415052	-0,80140371	-0,80140371	-0,2787536	-0,2787536	-0,80140371
-0,64640373	-1,30642503	-1,21642983	-0,64640373	0,200659451	-1,24846372	-1,47348697	-0,80140371	-0,70415052	-0,91539984	-1,00560945	-0,70415052	0,200659451	-0,10380372	-0,64640373

Este é o logaritmo com base 0,1

O que devo fazer com ele?

Eu tentei outras funções. Mas como posso entendê-los também?

O erro de cada módulo é dado como uma porcentagem. 0% é o resultado ideal" Número 1 significa 100% - x% ou 1-X*0,01

Alexandr Andreev 2020.06.06 21:19 #9

@Sergey Tabolin @Sergey Tabolin

															TOTAL
0,9557	0,8291	0,8418	0,9747	0,9937	0,8228	0,7152	0,943	0,8671	0,943	0,9177	0,9367	0,9937	0,9684	0,9304	0,77439
0,9494	0,8228	0,8734	0,962	0,9937	0,8038	0,7089	0,9557	0,9051	0,9494	0,9367	0,9367	0,981	0,981	0,9367	0,758606
0,9557	0,7975	0,8354	0,9557	0,9937	0,8228	0,7025	0,9367	0,9494	0,9177	0,8987	0,9494	0,9937	0,9873	0,9557	0,771806

a segunda linha é a melhor, e a primeira e a terceira são muito semelhantes

o total subtraído da unidade, ou seja, quanto mais próximo de 0 o total, melhor os resultados..... em outras palavras, os resultados até agora não são muito bons porque 0,75 é seu 75, embora dependa do que comparar com..... a pior pontuação seria 1 (100%) a melhor pontuação 0

Você tem que entender que uma pontuação de 90 é dez vezes melhor do que uma pontuação de 99.... uma pontuação de 99 é dez vezes melhor que uma pontuação de 99,9... 100 na verdade só é possível quando todos os módulos têm uma pontuação de erro de 100... Ou seja, uma pontuação de 0,1 é dez vezes pior que uma pontuação de 0,01. Ao mesmo tempo, uma pontuação de 10 é dez vezes pior que uma pontuação de 1.

com o logaritmo sobre pensar..... a resposta deve ser exclusivamente valores positivos... geralmente um logaritmo de 1.1... na faixa de 1 a 2, não 0 a 1.... se quiserem aumentar o número e de 2 se quiserem diminuir progressivamente

O método do desvio quadrático está definitivamente fora de questão. Assim como todos os outros que contam os desvios. Porque, idealmente, o desvio quadrático de uma regressão linear seria usado para entender a variância. Mas então obtemos uma estimativa desses desvios sem nenhuma média dos números em si.....

Practical advice, please. Existe um padrão para Aprendizado de máquina no

Roman 2020.06.07 01:48 #10

Сергей Таболин:

Pergunta: Como posso avaliar os resultados corretamente?

O erro de cada módulo é dado como uma porcentagem. 0% é o resultado ideal.

________________ PARÂMETROS ________________	Mod 1	Mod 2	Mod 3	Modo 4	Modo 5	(vi) Modo 6	(vi) Modo 7	(vi) Modo 8	(vi) Mod 9	(vi) Mod 10	(vi) Mod 11	(vi) Mod 12	(viii) mod 13	(vi) 14	Modo 15	Erro médio	Das tentativas
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_HAND	4,43	17,09	15,82	2,53	0,63	17,72	28,48	5,70	13,29	5,70	8,23	6,33	0,63	3,16	6,96	9,11	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT1	5,06	17,72	12,66	3,80	0,63	19,62	29,11	4,43	9,49	5,06	6,33	6,33	1,90	1,90	6,33	8,69	158,00
2_48_24_2160_12_VECTOR_UP_HIDDEN_LAYERS_MT2	4,43	20,25	16,46	4,43	0,63	17,72	29,75	6,33	5,06	8,23	10,13	5,06	0,63	1,27	4,43	8,99	158,00

Eu quero que o erro de cada módulo seja mínimo, mas também quero que a dispersão seja mínima.

É provavelmente melhor obter a soma dos quadrados para os erros do módulo, e extrair a raiz.
Assim, obteremos a estimativa de erro total do módulo.
Quanto mais perto de zero este valor estiver, melhor.
Portanto, é assim.

//+------------------------------------------------------------------+
//|                                                EstimateError.mq5 |
//|                        Copyright 2020, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2020, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"


double ModN[15][3] = {{4.43, 5.06, 4.43},
                      {17.09, 17.72, 20.25},
                      {15.82, 12.66, 16.46},
                      {2.53, 3.80, 4.43},
                      {0.63, 0.63, 0.63},
                      {17.72, 19.62, 17.72},
                      {28.48, 29.11, 29.75},
                      {5.70, 4.43, 6.33},
                      {13.29, 9.49, 5.06},
                      {5.70, 5.06, 8.23},
                      {8.23, 6.33, 10.13},
                      {6.33, 6.33, 5.06},
                      {0.63, 6.33, 0.63},
                      {3.16, 1.90, 1.27},
                      {6.96, 6.33, 4.43}};

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   double ModX[];
   ArrayResize(ModX, 3);
   ZeroMemory(ModX);   
   
   int    num = 1;
   double est = 0.0;
   
   for(int i=0; i<15; i++)
   {
      for(int j=0; j<3; j++)
      {
         ModX[j] = ModN[i][j];         
      }
         
      est = EstimateError(ModX);  
      
      PrintFormat("Mod"+(string)num+" EstimateError: %.3f", est); 
      num++;
   }         
}// End OnStart

//+------------------------------------------------------------------+
double EstimateError(double & arr[])
{
   int size = ArraySize(arr);
   if(size == 0 || size < 3) 
      return(0.0);
   
   //double avg       = ArrayMean(arr); 
   double max       = ArrayMax(arr);   
   double min       = ArrayMin(arr); 
   double sum_sqr_e = 0.0;
   double est_e     = 0.0;      
   
   
   for(int i=0; i<size; i++)   
      sum_sqr_e += MathPow(arr[i] - (max-min)/* или avg*/, 2.0) / (size - 2.0);
      
   est_e = MathSqrt(sum_sqr_e);   

   return(est_e);
}

//+-------------------------------------------------------------------
//Возвращает максимальное значение элементов массива
double ArrayMax(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);          
   
   double max = arrIn[0];
   for(uint i=1; i<size; i++)
      if(arrIn[i] > max) 
         max = arrIn[i];

   return(max);
}

//--------------------------------------------------------------------
//Возвращает минимальное значение элементов массива
double ArrayMin(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);   
   
   double min = arrIn[0];  
   for(uint i=1; i<size; i++)
      if(arrIn[i] < min) 
         min = arrIn[i];

   return(min);
}

//--------------------------------------------------------------------
//Возвращает средне арефметическое значение элементов массива
double ArrayMean(double & arrIn[])
{
   uint size = ArraySize(arrIn);
   if(size == 0) 
      return(0.0);         

   double sum = 0.0;       
   for(uint i=0; i<size; i++) 
      sum += arrIn[i];     
   
   return(sum/size);
}

//--------------------------------------------------------------------

2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod1 EstimateError: 6.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod2 EstimateError: 26.422
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod3 EstimateError: 19.577
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod4 EstimateError: 3.226
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod5 EstimateError: 1.091
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod6 EstimateError: 28.540
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod7 EstimateError: 48.234
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod8 EstimateError: 6.361
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod9 EstimateError: 6.102
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod10 EstimateError: 5.965
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod11 EstimateError: 8.130
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod12 EstimateError: 8.098
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod13 EstimateError: 7.198
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod14 EstimateError: 1.413
2020.06.07 04:59:23.227 EstimateError (AUDUSD,M5)       Mod15 EstimateError: 6.138

A estimativa mostra que o Mod5 tem o menor erro.

Etiqueta de mercado ou Como formar os valores Econometria: um passo à

1 2 3 4 5 6 7

Novo comentário