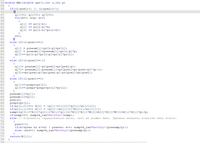
void calcPolynomialRegression(double &PricesArray[],double &RegressionArray[], int power) { ArrayResize(RegressionArray, ArraySize(PricesArray)); ArraySetAsSeries(RegressionArray,ArrayGetAsSeries(PricesArray)); double summ_x_value[21],summ_y_value[11],constant[11],matrix[11][11]; ArrayInitialize(summ_x_value,0); ArrayInitialize(summ_y_value,0); ArrayInitialize(constant,0); ArrayInitialize(matrix,0); double summ=0,summ_x=0,summ_y=0; int pos=ArraySize(PricesArray)-1; summ_x_value[0]=ArraySize(PricesArray); for(int exp_n=1; exp_n<=2*power; exp_n++) { summ_x=0; summ_y=0; for(int k=1; k<=ArraySize(PricesArray); k++) { summ_x+=MathPow(k,exp_n); if(exp_n==1) summ_y+=PricesArray[pos-k+1]; else if(exp_n<=power+1) summ_y+=PricesArray[pos-k+1]*MathPow(k,exp_n-1); } summ_x_value[exp_n]=summ_x; if(summ_y!=0) summ_y_value[exp_n-1]=summ_y; } for(int row=0; row<=power; row++) for(int col=0; col<=power; col++) matrix[row][col]=summ_x_value[row+col]; int initial_row=1; int initial_col=1; for(int i=1; i<=power; i++) { for(int row=initial_row; row<=power; row++) { summ_y_value[row]=summ_y_value[row]-(matrix[row][i-1]/matrix[i-1][i-1])*summ_y_value[i-1]; for(int col=initial_col; col<=power; col++) matrix[row][col]=matrix[row][col]-(matrix[row][i-1]/matrix[i-1][i-1])*matrix[i-1][col]; } initial_col++; initial_row++; } int j=0; for(int i=power; i>=0; i--) { if(j==0) constant[i]=summ_y_value[i]/matrix[i][i]; else { summ=0; for(int k=j; k>=1; k--) summ+=constant[i+k]*matrix[i][i+k]; constant[i]=(summ_y_value[i]-summ)/matrix[i][i]; } j++; } int k=1; for(int i=ArraySize(PricesArray)-1; i>=0; i--) { summ=0; for(int n=0; n<=power; n++) summ+=constant[n]*MathPow(k,n); RegressionArray[i]=summ; k++; } }
Eu implementei o cálculo de regressão (não apenas linear) sem nenhum ciclo. Mais precisamente, um ciclo é necessário apenas uma vez durante a inicialização.
Como resultado, a velocidade de cálculo é mil vezes mais rápida.
E o código é mais curto.
Mas desculpe, não vou postar o código. É um segredo.
Só estou dizendo que é real.
Há dois artigos que ajudarão

- www.mql5.com
Eu implementei o cálculo da regressão (não apenas linear) sem nenhum ciclo. Para ser mais exato, o laço é necessário apenas uma vez na inicialização.
Como resultado, a velocidade de cálculo é mil vezes mais rápida.
E o código é mais curto.
Mas desculpe, não vou postar o código. É um segredo.
Só estou dizendo que é real.
O código é muito simples. Adicionamos os quadrados atuais, subtraímos os quadrados fora do intervalo. É isso aí. Esse é todo o segredo).
Pode ser ainda mais interessante, mas seguindo princípios diferentes.
O código é muito simples. Adicionamos os quadrados atuais, subtraímos os quadrados fora do intervalo. É isso aí. Esse é o segredo).
Isso é engraçado ))
Para torná-lo ainda mais engraçado, você poderia dizer não sobre o canal, mas sobre como fazer uma linha de regressão polinomial sem ciclos. Mas eu definitivamente não vou fazer isso. Você não precisa disso.
Eu implementei o cálculo de regressão (não apenas linear) sem nenhum ciclo. Mais precisamente, o ciclo é necessário apenas uma vez na inicialização.
Como resultado, a velocidade de cálculo é milhares de vezes mais rápida.
E o código é mais curto.
Mas desculpe, não vou postar o código. É um segredo.
Só estou dizendo que é real.
Milhares de vezes mais rápido, e sem um loop de valores de entrada ???
Eu não acredito!!!
No mínimo, um loop de parâmetros de entrada é obrigatório !
Eu implementei o cálculo de regressão (não apenas linear) sem nenhum ciclo. Mais precisamente, o loop é necessário apenas uma vez na inicialização.
Como resultado, a velocidade de cálculo é mil vezes mais rápida.
E o código é mais curto.
Mas desculpe, não vou postar o código. É um segredo.
Só estou dizendo que é real.
E mesmo sem um laço de soma x*y? E se x e y não forem linhas retas?
Milhares de vezes mais rápido, e sem um loop de valores de entrada ???
Eu não acredito!!!
Ao menos um loop sobre os parâmetros de entrada é obrigatório !
E mesmo sem um laço de soma x*y ? E se x e y não forem linhas retas?
Não acredite nisso por todo o seu valor.
Rashid deixou cair os artigos. Leia-os com atenção. Há ali um link para outro artigo:
https://www.mql5.com/ru/articles/270
Se você abana seu cérebro ao nível da matemática do 7º-8º ano, você pode obter o desvio padrão para obter o canal, não apenas a média deslizante, de forma semelhante, sem um ciclo. Tenho isto implementado para um polinômio de qualquer grau, não apenas o primeiro grau (regressão linear). Você pode senti-lo na versão de demonstração no mercado.
HH Eu escrevi que o laço é necessário uma vez na inicialização.
Milhares de vezes mais rápido - isto inclui o cálculo do desvio padrão (ou seja, largura do canal)- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Eu tenho um indicador de regressão linear.
Como construir seu cálculo na EA e obter dados em 0 barra ou em 1.
Eu tentei fazer assim:
Mas não dá algo...