[Arquivo!] Pura matemática, física, química, etc.: problemas de treinamento do cérebro não relacionados ao comércio de qualquer forma - página 313
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - resposta única
Se qualquer peso for inferior a 2^n, o peso total será inferior a 63,
Se mais, haverá lacunas na seqüência de pesos que podem ser obtidas com estas chaleiras.
Curiosamente, o problema se torna consideravelmente mais difícil e interessante se os pesos puderem ser colocados em ambas as xícaras ao mesmo tempo. Esse é o que eu gostaria de torturar. Mas eu não conheço a solução.
Embora, de qualquer forma, se verifique que o peso mínimo dos pesos é 1. Mas isto não significa automaticamente que eles vão ao grau de 2.
Próximo (10):
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Não tenho certeza sobre o mínimo de chaleira 1
talvez duas chaleiras 2 e 3 também funcionariam.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
O computador fez as contas :)
Se os pesos podem ser colocados em ambos os copos simultaneamente, o problema tem 2136 soluções (exatamente 63 pesos podem ser equilibrados).
Na verdade, todas as soluções contêm um peso de 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
Você vai postar o programa? Por favor, por favor!
Sim, peça por um programa com lágrimas.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
Eu estava errado sobre 1.
Não há nada de interessante no programa, um simples exagero.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT];
for(int i=0;i<COUNT;i++) arr[i]=false;
// 1 - em um copo, 0 - o peso não está envolvido -1 - no segundo copo
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) return false;
if(ves>0) arr[ves-1]=true;
}
for(int i=0;i<COUNT;i++)
se(!arr[i]) devolver falso;
retornar verdadeiro;
}
principal(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5);
}
Следующая (10-й):
A prova é sem muito rigor, mas correta.
Vamos introduzir a notação de coordenadas de vértices, como mostra a figura. Para que o azul seja um quadrado
x1-x2=y1-y4 ;
y1-y2=x1-x2;
bem como
x3-x4=y2-y3;
y4-y3=x2-x3.
A partir das duas primeiras equações, se nos lembrarmos da equação gráfica, obtemos
x4-x2=A(sinx2-sinx4),
do terceiro e quarto
x3-x1=A(sinx1-sinx3).
Como não são impostas restrições aos quadrados além do número mínimo de quadrados, consideraremos apenas os casos em que os quadrados são simétricos quanto à origem. Mas depois x4=-x2, x3=-x1 e o mesmo com os pecados. Nossas equações tomarão a forma:
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Relembrar o gráfico das funções de x2 e x1 em pé do lado esquerdo. Para isso, olhe para a figura: o gráfico tem um extremo decrescente tanto no positivo como no negativo x. Obviamente, reduzindo gradativamente o número A, podemos obter tantas raízes quantas forem necessárias, inclusive 1978 e mais.
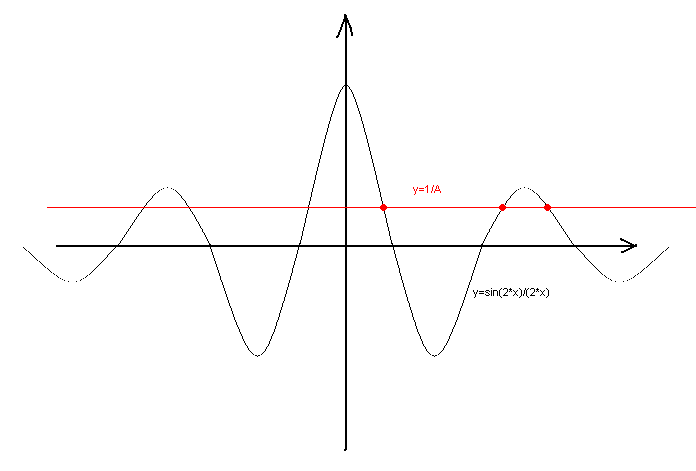
As raízes obtidas são diferentes, e se relacionam de forma puramente irracional. Não preciso provar detalhadamente que os quadrados, neste caso, não são iguais aos pares.