Denis, tenho este comentário sobre o artigo.
Quanto à teoria, não há dúvidas, tudo é apresentado em detalhes.
Quanto à prática, gostaria de chamar sua atenção para as figuras em que você mostra histogramas empíricos, especialmente a Figura 2. A questão é que você cometeu dois erros muito significativos em sua análise.
Em primeiro lugar, você definiu um número muito pequeno de classes para o script que gera os histogramas - apenas 9, o que, por si só, é um grande golpe no poder do critério de Pearson e torna sua aplicação ineficaz. No futuro, use de 200 a 300 classes para ter certeza de que, se o tamanho da amostra permitir (e ele permite), você não cometerá um erro. Se você tivesse feito exatamente isso, poderia ter certeza de que o teste para a distribuição lognormal teria dado um resultado negativo, assim como o teste de retornos para hipersecanos. A propósito, é muito fácil certificar-se de que duas dessas distribuições não podem representar simultaneamente um determinado valor e seu módulo, basta pegar a "metade" da hipersecância e convoluí-la com ela mesma (análogo a pegar o módulo de uma variável aleatória): você definitivamente não obterá uma lognormal.
A segunda imprecisão é que você não usou o conhecimento a priori de que o topo (também conhecido como expectativa) da distribuição de retornos deve estar exatamente em 0 (caso contrário, todos nós seríamos bilionários há muito tempo). É por isso que o histograma da Figura 2 parece deslocado para a direita, embora não devesse. Novamente, levar isso em conta ao traçar o histograma tornaria os testes mais confiáveis.
P.S. Estou escrevendo um artigo sobre os fundamentos da modelagem, daí o grande interesse. Obrigado por seu artigo, ele está no tópico. Atenciosamente.
...Em primeiro lugar, você definiu um número muito pequeno de classes para o script que gera os histogramas - apenas 9, o que, por si só, é um grande golpe no poder do critério de Pearson e torna sua aplicação ineficaz. No futuro, use de 200 a 300 classes para ter certeza de que, é claro, se o tamanho da amostra permitir (e ele permite), você não cometerá um erro. Se tivesse feito dessa forma, você poderia ter certeza de que o teste para a distribuição lognormal daria um resultado negativo, bem como o teste de retornos para hipersecanos. A propósito, é muito fácil ter certeza de que duas dessas distribuições não podem representar um determinado valor e seu módulo ao mesmo tempo, basta pegar a "metade" da hipersecância e convoluí-la com ela mesma (análogo a pegar o módulo de um valor aleatório): você definitivamente não obterá uma distribuição lognormal.
Caro alsu, obrigado por sua opinião!
Vamos por ordem.
O número de classes não é definido voluntariamente, mas de acordo com alguma fórmula. No meu caso, é a fórmula de Sturgis. É uma das regras mais populares. Não é perfeita, concordo com isso. Mas ainda assim...
E você faz 200-300 aulas de acordo com qual regra?
A segunda imprecisão é que você não usou o conhecimento a priori de que o topo (também conhecido como expectativa) da distribuição de retornos deve estar exatamente em 0 (caso contrário, todos nós seríamos bilionários há muito tempo). É por isso que o histograma da Figura 2 parece deslocado para a direita, embora não devesse. Novamente, levar esse ponto em consideração ao construir o histograma tornaria os testes mais confiáveis.
Eu analiso a amostra com base em fatos. Eu analiso o que tenho. E com base em que o topo da distribuição de rendimento deve estar exatamente no ponto 0? Talvez eu esteja entendendo algo errado...
Além disso, se você observar a distribuição para a qual o ajuste foi implementado (que foi X~HS(-0.00, 1.00)), é fácil ver que o primeiro parâmetro - o parâmetro de deslocamento - é exatamente 0. De fato, ele é igual à expectativa.
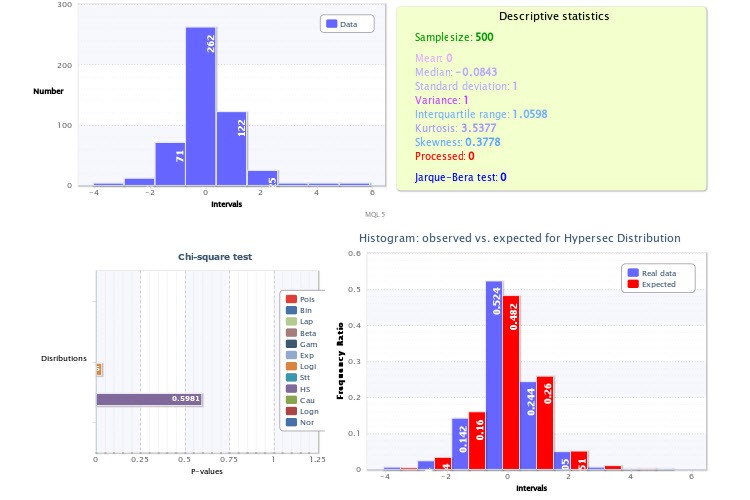
Aqui está outro relatório em html sobre a amostragem dos valores padrão. Espero que a figura esteja mais ou menos legível. Mas ela não é idêntica à do artigo. Peguei os dados mais recentes agora mesmo.
Como você pode ver, Média =0. E o melhor ajuste é a distribuição Hyperbolic Secant: X~HS(0.00, 1.00).
Exatamente, a fórmula de Sturges deu exatamente 9 classes, mas esse é um motivo para pensar em aumentar o tamanho da amostra (invertendo a fórmula, vejo que você a tem em torno de 256?).
Além disso, essa fórmula funciona bem apenas para populações gerais de distribuição normal (para a qual foi derivada) e, como é considerado, o tamanho da amostra não é superior a 200 valores. Você pode usar fórmulas alternativas - Diakonis, Scott....
Em geral, você sabe, Sturges nunca apresentou uma justificativa lógica para sua fórmula - sim, ela se baseia na aproximação da distribuição normal pela distribuição binomial, e daí? Como isso pode afetar a questão da eficiência da escolha do número de classes? O critério de otimização nunca foi definido pelo autor e a fórmula em si foi escrita ao acaso. Mas a questão é que, por muito tempo, a abordagem de Sturges foi a única formalizada de alguma forma e foi automaticamente (e, na minha opinião, de forma bastante impensada!) incluída em todos os pacotes estatísticos, o que, a propósito, é bastante irritante, precisamente porque essa fórmula quase sempre fornece um número extremamente subestimado de classes.
Mais uma vez, existem fórmulas alternativas, mas a presença de um computador pessoal, paradoxalmente, nos dá a oportunidade de usar nossa própria cabeça como um dispositivo, ou seja, uma maneira visual de determinar um número mais ou menos ideal de classes para essa amostra específica, quando, alterando suavemente esse indicador, conseguimos um compromisso entre a suavidade do gráfico e a resolução do histograma. A propósito, esse método geralmente é melhor e mais rápido do que qualquer fórmula.
Sempre digo a todos: antes de colocar números em fórmulas, pergunte o que significam e como (e se) devem ser aplicados. Em resumo, sou contra o uso da fórmula de Sturges, pois a considero desatualizada e inadequada).
Com relação à média. A expectativa de retorno deve estar em 0 porque, se não fosse assim, poderíamos estupidamente apostar sempre em uma direção, correspondente ao sinal desse MO, e ter a garantia de obter um retorno de qualquer tamanho predeterminado. Bem, o topo deve coincidir com o MO puramente por motivos de simetria: a metade esquerda do gráfico deve ser uma imagem espelhada da metade direita (o aumento e a diminuição da taxa são estatisticamente iguais e não deve haver diferenças entre eles), portanto, o centro de simetria coincide com o centro.
Como você usa HS(0.00, 1.00), portanto, deve centralizar as classes, ou seja, a classe zero deve incluir os valores de índice em algum intervalo simétrico (-x0;x0); caso contrário, introduzimos nos cálculos um erro sistemático associado ao deslocamento das classes em relação ao zero, que acaba se infiltrando no resultado do teste chi^2. Seu ponto 0 não está no meio da classe zero.
De fato, a questão de como tornar as classes simétricas em dados discretos não é nada trivial e, novamente, é bom resolvê-la para cada amostra específica individualmente e com muito cuidado, caso contrário, corremos o risco de obter resultados inadequados também devido à escolha errada dos limites da divisão em classes.
alsu, você tocou em um tópico que, embora não seja o assunto do meu artigo, é extremamente interessante. Na medida do possível, pesquisarei mais sobre esse assunto.
Obrigado por sua crítica construtiva!
Gostei da sua opinião sobre a aplicabilidade do conhecimento científico nas negociações.
Você poderia me dizer quais livros recomendaria para uma pessoa familiarizada com a teoria da probabilidade e a estatística matemática?
Denis, boa tarde.
Gostei de sua opinião sobre a aplicabilidade do conhecimento científico na negociação.
Por favor, diga-me qual dos livros você recomendaria para uma pessoa que está familiarizada com a teoria da probabilidade e a estatística matemática.
Obrigado por sua opinião!
Acho que se deve procurar algo para iniciantes, então, algum livro de literatura. O principal é que o texto do livro não deve desencorajá-lo a continuar lendo :-))).
Gostei de algo do Gaidyshev e de algo do Bulashev.....
- rsdn.org
A segunda imprecisão é que você não usou o conhecimento a priori de que o topo (também conhecido como expectativa) da distribuição de retornos deve estar exatamente em 0 (caso contrário, todos nós já seríamos bilionários há muito tempo).
De modo algum. Um deslocamento do topo da distribuição em relação a 0 (crescimento/declínio de um instrumento) não significa que ele será o mesmo no futuro. É por isso que a maioria dos traders não é bilionária, não porque.
Com os melhores cumprimentos.
...O fato de deslocar o topo da distribuição em relação a 0 (instrumento em ascensão/declínio) não significa necessariamente que esse será o caso no futuro...
Concordo.
Pergunta para alsu. Você quis dizer eficiência de mercado ao falar sobre o ponto zero?
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo O Papel das Distribuições Estatísticas no Trabalho de Negociaçã foi publicado:
Este artigo é uma continuação lógica do meu artigo de Distribuições de Probabilidade Estatística em MQL5 que apresenta as classes para trabalhar com algumas distribuições estatísticas teóricas. Agora que temos uma base teórica, sugiro que devemos prosseguir diretamente para conjuntos de dados reais e tentar fazer algum uso informativo desta base.
Autor: Dennis Kirichenko