좋은 질문) 이와 같은 그림(1에서 25까지) 대각선 xxx, 아무도 자신과 친구가되지 않습니다. Petya는 이것을해야하며 여전히 13 번 볼 수 있습니다)) 0에서 24까지의 경우 한 동급생을 무시할 수 있습니다. 우리는 24 * 24 및 12 X의 제곱을 얻습니다.
홀수 정사각형 크기, 대각선 = (N + 1) / 2, 짝수 N / 2. Petya를 고려하고 그를 제외하고 이것을 클래스의 차이로 상상할 수 있습니다.
내가 이해하지 못하는 유일한 것은 14 또는 2가 아니라 13이라는 것입니다. 순차적 마킹 절차로 전체 mosch를 부드럽게 만들었습니다. 그러나 아마도 그 안에 왜 정확히 13인지에 대한 설명을 찾아야 할 것입니다. :)
그건 그렇고, 당신은 그것을 명명하지 않고 Dirichlet 원리를 사용했습니다.
사실은 이 마크업을 사용하면(그리고 단 하나의 원칙만 따릅니다. 모든 사람은 친구 수가 다르기 때문에 매우 일반적입니다.) Petya는 전혀 참여하지 않습니다. 그는 26명의 학생 중 한 명으로, 나머지 학생들과 절대적으로 동등합니다. 결과적으로, 모든 사람이 다른 수의 친구를 가질 수 없다는 것이 밝혀졌습니다. 1에서 N-1까지의 시리즈는 N개의 다른 숫자로 연속적으로 번호가 매겨질 수 없습니다(이것은 증명의 끝 부분에 있음). 따라서 두 학생은 같은 수의 친구가 있어야 합니다. 그리고 이 두 학생은 줄 중앙에서 서로 옆에 있습니다. 따라서 Petya는 이 둘 중 하나임이 틀림없습니다. 이 경우에만 다른 모든 사람들에게 다른 수의 친구가 있습니다. 다른 마크업은 이 조건을 충족할 수 없습니다.
중앙에 손으로 표시하려고하면 모든 것이 직접 표시됩니다.
Swan 의 테이블이 이를 보여줍니다.
귀하의 질문을 올바르게 이해했기를 바랍니다.
제 생각에는 디리클레 원리를 사용하지 않고 그 특수한 경우에 대한 기초적인 증거를 제시했습니다.
이러한 요청은 무엇입니까? 당신은 당신의 요청을 다시 읽고, 요청은 요청입니다, - 나는 첫 번째 문장에 갇혔고, "어떤 것 다음에 어떤 것"이라는 생각의 발전은 나를 완전히 끝냈습니다.
추신: 나침반이 없는 것이 아쉽습니다. 좋은 점 - 그것은 세계의 다른 방향, 모든 종류의 방향을 보여줍니다 ...
글쎄요, 아아, 여기서 할 말은 없습니다. :(
글쎄요, 아아, 여기서 할 말은 없습니다. :(
나침반에 대해? - 농담이야, 나는 그것이 당신의 "사이코 타입"에 적합하다고 생각했습니다. :에 대한)
Alexei , 내 결정에 만족합니까?
7번(일반이 아니라 동급생 25명의 특별한 경우)에 너무 쿨하다고 생각하시나요?
네, 7일차에는 아마도 멋질 것입니다. 하지만 초등, 그리고 그것은 기쁘게 생각합니다.
Yurixx 는 >> 두 요소의 값이 같아야 합니다.
N=26(즉, 수업에 연결이 없는 학생이 없음)에 대해 이 반복된 숫자 = 13임을 확인하는 것은 쉽습니다.
내가 이해하지 못하는 유일한 것은 14 또는 2가 아니라 13이라는 것입니다. 순차적 마킹 절차로 전체 mosch를 부드럽게 만들었습니다. 그러나 아마도 그 안에 왜 정확히 13인지에 대한 설명을 찾아야 할 것입니다. :)
그건 그렇고, 당신은 그것을 명명하지 않고 Dirichlet 원리를 사용했습니다.
그리고 왜?
좋은 질문)
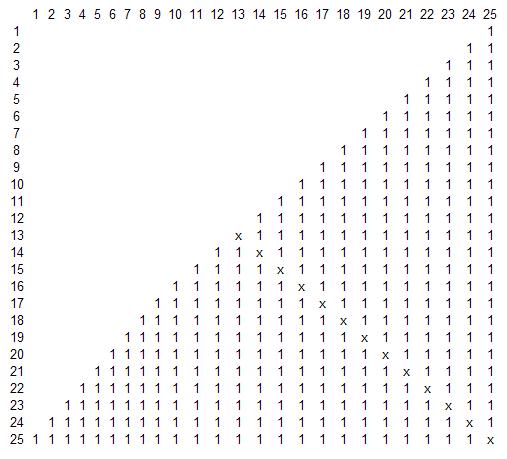
이와 같은 그림(1에서 25까지)
대각선 xxx, 아무도 자신과 친구가되지 않습니다. Petya는 이것을해야하며 여전히 13 번 볼 수 있습니다))
0에서 24까지의 경우 한 동급생을 무시할 수 있습니다. 우리는 24 * 24 및 12 X의 제곱을 얻습니다.
홀수 정사각형 크기, 대각선 = (N + 1) / 2, 짝수 N / 2.
Petya를 고려하고 그를 제외하고 이것을 클래스의 차이로 상상할 수 있습니다.
확실한 증거는 아닌 것 같습니다. 이것은 정확히 12 또는 13인 이유를 명확하게 설명하지 않고 손가락으로 그린 그림입니다. 좋습니다. 생각해보자.
내가 이해하지 못하는 유일한 것은 14 또는 2가 아니라 13이라는 것입니다. 순차적 마킹 절차로 전체 mosch를 부드럽게 만들었습니다. 그러나 아마도 그 안에 왜 정확히 13인지에 대한 설명을 찾아야 할 것입니다. :)
그건 그렇고, 당신은 그것을 명명하지 않고 Dirichlet 원리를 사용했습니다.
사실은 이 마크업을 사용하면(그리고 단 하나의 원칙만 따릅니다. 모든 사람은 친구 수가 다르기 때문에 매우 일반적입니다.) Petya는 전혀 참여하지 않습니다. 그는 26명의 학생 중 한 명으로, 나머지 학생들과 절대적으로 동등합니다. 결과적으로, 모든 사람이 다른 수의 친구를 가질 수 없다는 것이 밝혀졌습니다. 1에서 N-1까지의 시리즈는 N개의 다른 숫자로 연속적으로 번호가 매겨질 수 없습니다(이것은 증명의 끝 부분에 있음). 따라서 두 학생은 같은 수의 친구가 있어야 합니다. 그리고 이 두 학생은 줄 중앙에서 서로 옆에 있습니다. 따라서 Petya는 이 둘 중 하나임이 틀림없습니다. 이 경우에만 다른 모든 사람들에게 다른 수의 친구가 있습니다. 다른 마크업은 이 조건을 충족할 수 없습니다.
중앙에 손으로 표시하려고하면 모든 것이 직접 표시됩니다.
Swan 의 테이블이 이를 보여줍니다.
귀하의 질문을 올바르게 이해했기를 바랍니다.
제 생각에는 디리클레 원리를 사용하지 않고 그 특수한 경우에 대한 기초적인 증거를 제시했습니다.
개인적으로 마음에 들었습니다.
우아하게.
그것은 나에게 재빠른 작은 Gauss와 반원들에게 1에서 99까지의 숫자를 더하라고 요청했고 잠시 동안 떠날 예정이었던 교사에 관한 우화를 생각나게 했습니다 - 아이들이 더하는 동안.
그들은 이미 곱셈을 알고 있었지만 반복은 학습의 어머니 ...
Gauss는 교사를 끊었습니다. 대답은 즉시 받았습니다.
;)
Swetten 은 우리에게 가장 친절합니다.
:)
N명의 직원으로 구성된 팀에서 모든 사람이 다른 수의 친구를 갖는 상황은 있을 수 없습니다.
그러나 "두 사람은 같은 수의 친구를 가질 수 있습니다"를 추가하면 문제가 없습니다.
Petya를 이 두 가지 중 하나로 불러야 합니다.
예, 거의 그렇습니다.
문제의 조건을 법적으로 읽으면 Petya는 서로 같은 수의 친구를 가질 수 있습니다.
나는 상황을 읽을 때 - 이 작업은 올바르지 않다고 말했습니다. 나는 아마 그것을 증명할 수 있고 여러 면에서. 하지만 난... 아직.