記事"マーケット価格予測に対する汎用回帰モデル"についてのディスカッション - ページ 8 12345678 新しいコメント Andrey Dik 2011.03.17 13:58 #71 yosuf: プライベート・メッセージでご連絡ください。 指標は有料ですか? Yousufkhodja Sultonov 2011.06.13 20:27 #72 lyvel: Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите? Опубликован в кодбазе, пользуйтесь на здоровье! Yousufkhodja Sultonov 2011.06.13 20:28 #73 joo: 指標は有料か何か? コードベースに公開されているので、思う存分使ってください! flourishing 2012.01.12 05:15 #74 Rosh:新しい記事「市場価格予測のためのユニバーサル回帰モデル」が掲載されました:著者Юсуфходжа 良い記事だ。 非常に印象的 TipMyPip 2013.05.27 12:23 #75 素晴らしい!あなたの知識を提供し、私たちの取引を向上させる大きな心を持っていることに感謝します。 Renat Akhtyamov 2015.07.17 23:44 #76 残念なことだが、冒頭に間違いがある。まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的 回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、我々はまだ定義していない。まあ、一般的には。 Yousufkhodja Sultonov 2015.07.18 16:15 #77 new-rena:残念なことだが、冒頭に間違いがある。まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、私たちはまだ定義していない。まあ、一般的には...1.Doは価格の増分ではなく、時間t=0における価格に影響を与える力の初期ポテンシャルである。2.記事より:"...均衡状態にある市場価格は、ある外力D(t)の作用下でのみ変化しうると仮定する。 また、この力の影響の始まりから時間tの経過に伴う市場価格の変化P(t)は、まだ知られていない何らかの規則性によってゼロ値から連続的に増加し、無限大の値P(∞)=D0に達する傾向があると仮定しよう。すなわち、D0とは、この影響力の性質と符号に応じて、市場価格の有限の増加または減少を意味する。 さらに、D(t=0) = D0と仮定する。さらに、無限小の時間dtの間に、影響力は、時間tの瞬間までに残っている力D(t)に比例して、値dD(t)だけ減少すると仮定しよう: したがって、D(t)の時間tに対する指数関数的な依存性が得られる: (1) ここで t - 不安定化力の影響開始からの時間、時系列単位、秒(分、時、日、週、数十年、月、年); τ(tau)-比例係数、数値的にはプロセスの時定数に等しい、sec.(min,hours,days,weeks,decades,month,years)"。どこから1/s^2の次元性を見つけたのですか?その比に次元性はない。私は、ある過程に作用する力の変化(減少)速度は、力そのものに比例する、という仮説を立てた。比例係数として、時間の逆数次元を持つ比a(α)=1/tauを導入した。a (α)とは、システムのインピーダンス、つまりプロセスの流れに対するシステムの抵抗を意味し、tauとは、後に判明するように、ラプラス変換における時間のイメージであり、プロセスの分析を微分領域から通常の領域へと移行させるものである。つまり、どのような過程にも私たちとは異なる独自の時間が存在し、タウは時間の「翻訳者」として機能するのである。記事の中で、タウを推定する方法を紹介した:さて、時間tの対応する瞬間に対する関数fの値がわかっていれば、この式からパラメータn、τ、係数βは次のように決定される: (12) (13) (14) ここで 時間tと時間tの対応する瞬間に対する関数fの値は、区間の中間を参照した数値微分による不安定化の始まりから時間h0、h1、...、kの瞬間までの市場価格P0、P1、...、Pkの実際の値によって決定される: f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); など; t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; など。 Discussion of article "Universal マーケット価格予測に対する汎用回帰モデル 特定のディストリビューション法によるカスタムシンボルを用いた時系列モデリング 12345678 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
プライベート・メッセージでご連絡ください。
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
指標は有料か何か? コードベースに公開されているので、思う存分使ってください!
新しい記事「市場価格予測のためのユニバーサル回帰モデル」が掲載されました:
著者Юсуфходжа
良い記事だ。
非常に印象的
残念なことだが、冒頭に間違いがある。
まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。
次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。
そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的 回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、我々はまだ定義していない。
まあ、一般的には。
残念なことだが、冒頭に間違いがある。
まず、ある時刻tにおける価格の増分はもちろん何らかの値を持ち、それをD0とする。と仮定しよう。
次にt=0の時点では、価格への影響はなく、外部からの影響による価格上昇もないらしいことは理解できる。しかし、我々は再びデルタをD0と呼びました。
そして、dt/tauを式に入れましたが、これはいずれにせよ1/C^2です。 つまり、インパクトに加速度を与え、幾何学的回帰を動かすことになります。 なぜそうしなければならないのでしょうか?結局のところ、私たちはまだ定義していない。
まあ、一般的には...
1.Doは価格の増分ではなく、時間t=0における価格に影響を与える力の初期ポテンシャルである。
2.記事より:"...均衡状態にある市場価格は、ある外力D(t)の作用下でのみ変化しうると仮定する。
また、この力の影響の始まりから時間tの経過に伴う市場価格の変化P(t)は、まだ知られていない何らかの規則性によってゼロ値から連続的に増加し、無限大の値P(∞)=D0に達する傾向があると仮定しよう。すなわち、D0とは、この影響力の性質と符号に応じて、市場価格の有限の増加または減少を意味する。
さらに、D(t=0) = D0と仮定する。さらに、無限小の時間dtの間に、影響力は、時間tの瞬間までに残っている力D(t)に比例して、値dD(t)だけ減少すると仮定しよう:
したがって、D(t)の時間tに対する指数関数的な依存性が得られる:
ここで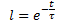
t - 不安定化力の影響開始からの時間、時系列単位、秒(分、時、日、週、数十年、月、年);
τ(tau)-比例係数、数値的にはプロセスの時定数に等しい、sec.(min,hours,days,weeks,decades,month,years)"。
どこから1/s^2の次元性を見つけたのですか?その比に次元性はない。私は、ある過程に作用する力の変化(減少)速度は、力そのものに比例する、という仮説を立てた。比例係数として、時間の逆数次元を持つ比a(α)=1/tauを導入した。a (α)とは、システムのインピーダンス、つまりプロセスの流れに対するシステムの抵抗を意味し、tauとは、後に判明するように、ラプラス変換における時間のイメージであり、プロセスの分析を微分領域から通常の領域へと移行させるものである。つまり、どのような過程にも私たちとは異なる独自の時間が存在し、タウは時間の「翻訳者」として機能するのである。記事の中で、タウを推定する方法を紹介した:
さて、時間tの対応する瞬間に対する関数fの値がわかっていれば、この式からパラメータn、τ、係数βは次のように決定される:
ここで
時間tと時間tの対応する瞬間に対する関数fの値は、区間の中間を参照した数値微分による不安定化の始まりから時間h0、h1、...、kの瞬間までの市場価格P0、P1、...、Pkの実際の値によって決定される:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); など;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; など。