どちらが良いかは、非常に難しい問題です。経験的リスク最小化と呼ばれるアプローチの1つは、Wapnickの著書「Algorithms and programs for dependence reconstruction」で展開されている。1972年のようです。
経験的リスクの尤度最大化/最小化というのは、私の理解では、対応するアルゴリズムの一般名称に過ぎません。私はアルゴリズム自体を必要としません、私はただ、できれば迅速かつ多様にカーブを修正し、新しいポイントで補間値を見つける可能性が必要です(スプラインパッケージは後者を可能にします)。
経験的リスクの尤度最大化/最小化というのは、私の理解では、対応するアルゴリズムの一般名称に過ぎません。私はアルゴリズムそのものを必要としません、私はただカーブを修正する必要があり、できれば高速で可変で、新しい点での補間値を見つけることが可能です(スプラインパッケージは後者を可能にします)。
最尤法も最小化(確か経験則ではなく平均値)リスクも、アルゴリズムの名前ではなく、問題設定における目標設定の方法です。もし目標が達成可能であれば、それは必然的に目標と一致する何らかのアルゴリズムを生じさせ、特定のケースでその達成を実現するものである。目標もそれを達成するアルゴリズムも必要ないのであれば、補間関数を選ぶという作業には何のアドバイスもできない。あなたの心のままに選んでください...。
任意に設定した関数を補間する必要があるので、スプラインを選択しました。
ノード ポイントの数によって補間量が異なることは正しく理解できたのですが、他に何を変化させればよいのでしょうか?
また、2つ目の質問ですが、初期系列の多くの異なる補間を構築するだけでよい場合、リストから 何を選択して補間を行えばよいのでしょうか(変動性が重要です)。
トレーダーにとって最も価値があるのは、補間でも近似でもなく、外挿である。
スプラインは外挿に適さない。
多項式近似・外挿の経験が豊富で、よく理解しています。経験が少ないのはフーリエです。
多項式による外挿とフーリエ法による外挿は全く性質が異なる。フーリエ外挿は、その周期性(この線は周波数、位相、振幅の異なる正弦波の和)からフラットな市場にしか適用できず、常に戻る傾向があるのに対し、多項式外挿は逆に、その次数性から常に「上に飛ぶ」「下に飛ぶ」傾向があり、トレンドに適して います。
したがって、良い外挿結果を得るためには、この2つの方法を組み合わせることが理にかなっています。
多項式近似は、この種の近似は非常によく最適化されており、非常に高速に計算できるため、プログラマーにとって特に興味深いものである。係数の計算のためのサイクルからなんとか抜け出した。
また、どのような近似法でも、新しい点ができるたびに再描画可能な線ができることも覚えておくとよいでしょう。近似線からのトレーサーのみ再描画されない。
多項式近似は、フーリエ近似と異なり、解が1つしかない。これにより、再描画不可能なユニークなスライドを作成することができます。
なるほど、適当に当てるのも悪くはないですね。だから、誰も同じような問題を解決していないのです。ビジュアライズしてみる、見てみる。
誰も解決していない-間違っているすべての補間手法は理論的に正当化され、通常は明確な目的があります。例えば、三次欠損の2本のスプラインは、スプラインの節で板に打ち付けた釘を通過する定規の弾性曲げの位置エネルギーを最小にする。このようにして、船の外形や翼の形状を描いた図面の点の表から、滑らかな(欠陥が3以下の)曲線を得ることができた。同じスプラインで、レジリエンス数学のマルチサポートビームのたわみを表現しています。多くの場合,補間節点での座標変位の和を最小にすることが目標となるが,異なる目標で補間した結果を比較するためには,一般化目標,つまりどのような補間方法でも計算可能な基準が必要である.決定される係数の数に基づいています。大雑把に言うと、多項式の次数を3から7に上げた近似で偏差の二乗和が20%減るなら、次数3が7より合理的ということになる。ラジオ工学におけるアナログは、私が混乱していなければ、フィルタのカットオフ周波数である。
トレーダーにとって最も価値のあるものは、補間や近似ではなく、外挿である。
スプラインは外挿に適さない。
多項式近似・外挿の経験が豊富で、よく理解しています。経験が少ない - フーリエ
多項式による外挿とフーリエ法による外挿は全く性質が異なる。フーリエ外挿は、その周期性(この線は周波数、位相、振幅の異なる正弦波の和)からフラットな市場にしか適用できず、常に戻る傾向があるのに対し、多項式外挿は逆に、その次数性から常に「上に飛ぶ」「下に飛ぶ」傾向があり、トレンドに適して います。
したがって、良い外挿結果を得るためには、この2つの方法を組み合わせることが理にかなっています。
多項式近似は、この種の近似は非常によく最適化されており、非常に高速に計算できるため、プログラマーにとって特に興味深いものである。係数の計算のためのサイクルからなんとか抜け出した。
また、どのような近似法でも、新しい点ができるたびに再描画可能な線ができることも覚えておくとよいでしょう。近似線からのトレーサーのみ再描画されない。
多項式近似は、フーリエ近似と異なり、解が1つしかない。これにより、再描画不可能なユニークなスライドを作成することができます。
それでいいんです。私には外挿するものがない。必要なのは内挿である。そのような外挿を前提に予測を立てるのは意味がないということです。このラインは、ブルーラインと同じように、できるだけ左右に強くする必要があります。そして、新しいポイントで解を求めたいのです、はい(既存の計算式に基づいて再計算することなく)。
そこで、多項式とスプライン、あるいはその亜種を使うのが良いのか、という質問です。あと、10次も楽しいかもしれませんね。
誰も解決していない......それがいけないんです。すべての補間手法は理論的に正当化され、通常は明確な目的があります。例えば、三次欠損の2本のスプラインは、スプラインの節で板に打ち付けた釘を通過する定規の弾性曲げのポテンシャルエネルギーを最小にする。このようにして、船の外形や翼の形状を描いた図面の点の表から、滑らかな(欠陥が3以下の)曲線を得ることができた。同じスプラインで、レジリエンス数学のマルチサポートビームのたわみを表現しています。多くの場合,補間節点での座標変位の和を最小にすることが目標となるが,異なる目標で補間した結果を比較するためには,一般化目標,つまりどのような補間方法でも計算可能な基準が必要である.決定される係数の数に基づいています。大雑把に言うと、多項式の次数を3から7に上げた近似で偏差の二乗和が20%減るなら、次数3が7より合理的ということになる。ラジオ工学におけるアナログは、私が混乱していなければ、フィルタのカットオフ周波数である。
ただ、これでやろうと思っていることを全部説明しようとし始めると、また数ページになってしまうのですが......)可変性、多項式の次数の違い、格子点の数などが必要です。
それでいいんです。私には外挿するものがない。必要なのは内挿である。そのような外挿での予測は、後から行っても意味がないという意味で。この線は、青い線と同じように、できるだけ左右に累進させることが必要です。そして、新しいポイントで解を求めたいのです、はい(既存の計算式に基づいて再計算することなく)。
そこで、多項式とスプライン、あるいはその亜種を使うのが良いのか、という質問です。あと、10度目もかっこいいかも。
まさに補間?本当ですか?近似ではなく?しかも再描画不可?
ティックごとに補間するわけではないんですね。
再描画せずに中間ノード(例えばZigZagノード)で補間が必要な場合、要は次のノードがどこになるかということです。
再描画できないクリアジグザグは、タイムマシンを持っていないと作れません。現在のバーが極限であることをタイムマシンなしで判断できるわけがないのです。
この掲示板には定期的に「ポニーテールの描き直し」と呼んでいる方がいらっしゃいます。
ポイントは、ポニーテールです。
SMAを半周期左にずらし、その半周期を偶然にもある程度の多項式で描き終えるというのは、このジャンルの古典的な手法である。例えば、https://www.mql5.com/ru/forum/224374。 すでにご覧になった方も多いと思います。
スプラインを使えば、ジグザグの極限に沿って非常にきれいに補間することができますが、最後の2〜3個のノードの間に再描画が発生することを明確に理解する必要があります。これなくして道はない!
再描画しない場合は、補間ではなく、近似線からのトレースと呼んでいます(補間ではありません!)。
多項式は別として、今のところ理解できるものはないですね。
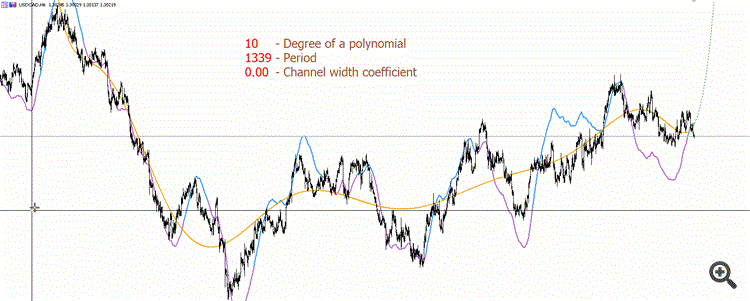
高次の多項式(10)の例を示すために、特別に記録したgifを示します。)
紫と青のラインは再描画できません。紫が「下を向いている」多項式、青が「上を向いている」多項式です。
また、高次の多項式の計算には十分な精度がない。高精度の型を使用する特別なライブラリを使用する必要があります。gifの小さな周期で「トレーサー」が「ジャンプ」し始めること、これがdoubleの精度を欠く理由です。
しかし、個人的には5次以上の多項式は実用に耐えるとは思えません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
任意に設定した関数を補間する必要があるので、スプラインを選択しました。
ノード ポイントの数によって補間量が異なることは正しく理解できたのですが、他に何を変化させればよいのでしょうか?
また,2つ目の質問ですが,元の系列を何通りにも補間する必要がある場合,リストから 何を選択するのが良いでしょうか(バリエーションが重要です)。