を含む2本の平行線間の距離を計算する!
グラフの縮尺を含めて（縮尺に影響されないように）2本の平行線間の距離を計算する方法を教えてください。
以下はその一例です。
赤い線は平行な2本の線の距離ですが、どのように計算するのでしょうか？
X軸の1点での距離を測定する必要があります。これはあなたの時間だと思いますが...。
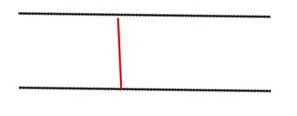
それとも、実際にオフセットで測定する必要があるのでしょうか？ピタゴラスの定理で、2つの辺と1つの角度を知っている...。
また、距離にもよりますが、ピクセル単位ですか？そうすると、そもそもすべてを適切な座標系に変換する必要がありますね。スケールに影響を与えないためには、グラフのスケールを固定で使用する必要があります。そうでなければ、必ず影響を受けてしまいます。
こんにちは。
また、そのような座標系はどのように構築されるのでしょうか、どのように想像されますか？
X軸の1点での距離を測定する必要があり、それがあなたの時間だと思うのですが......。
それとも、実際にオフセットで測定する必要があるのでしょうか？ピタゴラスの定理で、2つの辺と1つの角度を知っている...。
また、その距離がどれくらいかにもよりますが、ピクセル単位ですか？そうすると、まずはすべてを適切な座標系に変換する必要があります。論理的に考えれば、赤い線は2本の線（黒い線）に対して垂直であるべきで、それが距離を測ることになるのです。この値がどのような値で測定されるかは私には重要ではなく、最も重要なことは、スケールを変えてもこの値が変化しないことです。
ラインクロスの値を取って、その間のバーの 数を数えるというやり方もやってみたのですが．この方法は、スケールを変更するのには適していません !
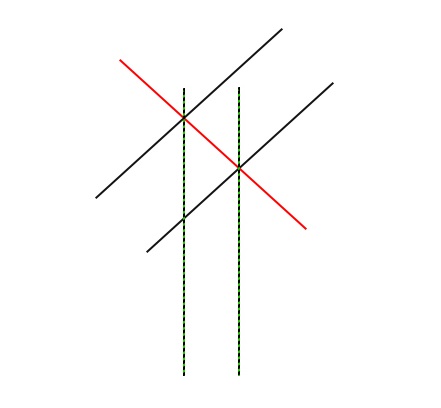
スケールの影響を受けないようにするには、チャートスケールを固定で使用する必要があります。そうでなければ、必ず影響を受けてしまいます。
なぜ？比率は？
Itum:
私は、この値がどのような値で測定されるかは気にしません。私にとって最も重要なことは、この値がスケールを変えても変化しないことです。
その場合は、pipsで測ればいいのです。線は価格に固定されており、スケールを変えても線間の距離は変わらず、線の視覚的表現が変わるだけです。
異なる縮尺の線のスクリーンショットで確認しましたが、ご覧の通り、線と線の間の距離は変わりません。
この場合の問題は、価格/秒の空間では点間の距離が定義されていないことです。したがって、最短距離を求めることはできない。
これは、軸の寸法が異なるからです。だから、どちらかでなければならない。
- 価格と時間の間に係数Xを選ぶと、距離は単位が( 価格×秒×X )の平方根と なる。
- は、1つの軸に沿った距離を数える。
垂直方向の距離は、チャートのタイムフレームと ほとんど変わりません（不完全なバーと週末のバーがあるためだけです）。
水平方向の距離は全く変わりません。
しかし、一軸で距離を測ると無限大になることがあり、これは意味がありません。
グラフの縮尺を含めて（縮尺に影響されないように）2本の平行線間の距離を計算する方法を教えてください。
以下はその一例です。
赤い線は平行な2本の線の距離ですが、どのように計算するのでしょうか？
初歩的なことだ ワトソン・・・
もし、価格× 時間の2次元系を平面価格× 価格に当てはめるなら、より論理的に価格変化の速度Vと呼ばれる新しい特性を導入しなければならない。
そして、1秒あたりの単位で測れるのが便利です。
そして、V＝自分の直線の角度の正接は、これに正比例する系にある。
- 垂直方向に1ピクセル＝1ポイント
- 横1ピクセル＝1秒（画面上では1分バーが60ピクセル幅になります。）
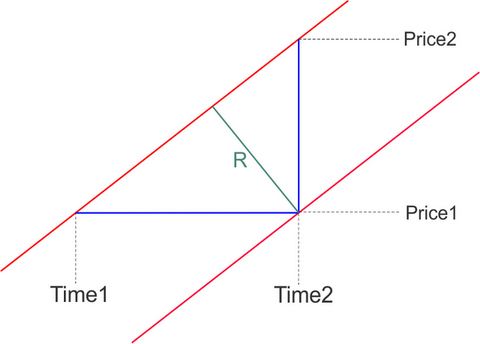
そうすると、2本の平行線の距離は2つの方法で計算できることになります。
double V=(Price2-Price1)/(Time2-Time1); ulong DeltaTime = TimeLine2-TimeLine1; // double DeltaPrice = PriceLine2- PriceLine1; double R=DeltaTime*V/sqrt(1+V*V) ; // double R=V/(DeltaPrice*sqrt(1+V*V)) ; // где // точки (Price1,Time1) и (Price2,Time2) это две любые точки лежащие на одной из параллельных линий, Time измеряется в секундах // TimeLine1 и TimeLine2 - время первой и второй линии при фиксированной цене (пересечение с горизонтальной линией) // PriceLine1 и PriceLine2- цена первой и второй линии при фиксированном времени (пересечение с вертикальной линией) // DeltaPrice - расстояние между линиями в пунктах по вертикали // DeltaTime - расстояние между линиями в секундах по горизонтали // R - искомое кратчайшее расстояние между двумя параллельными линиями, скорость измерения цены которых равна V пунктов в секунду
この垂直は、上記の系と異なる比率の系では、垂直に見えないことは明らかである
初歩的なことだ ワトソン・・・
価格× 時間の2次元システムを価格×価格の 平面に持ってくるためには、より論理的に価格変化の速度Vと呼ばれる新しい特性を導入する必要がある。
そして、1秒あたりの単位で測れるのが便利です。
そして、V＝自分の直線の角度の正接は、これに正比例する系にある。
- 垂直方向に1ピクセル＝1ポイント
- 横1ピクセル＝1秒（画面上では1分バーが60ピクセル幅になります。）
そうすると、2本の平行線の距離は2つの方法で計算できることになります。
この垂直は、前述した比率の異なる系では、垂直として現れないことは明らかである
Time1=TimeLine1、Time2=TimeLine2の場合があるので、これを単純化することができる。
それから。
double V=(Price2-Price1)/(Time2-Time1); double R=(Price2-Price1)/sqrt(1+V*V) ;
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
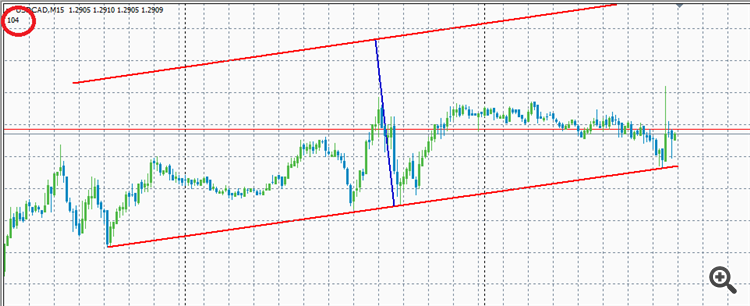
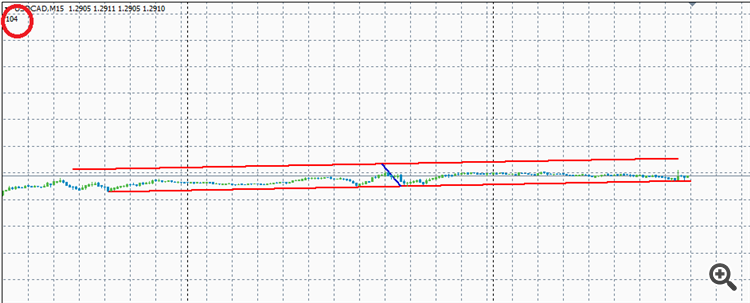
グラフの縮尺を含めて（縮尺に影響されないように）2本の平行線間の距離を計算する方法を教えてください。
以下はその一例です。
赤い線は平行な2本の線の距離ですが、どのように計算するのでしょうか？