賃借人 - ページ 19

新しいコメント
 

Sorento:

В чём другое? Ведь требуется строго больше. :)

まあ、神頼み、厳密にはそうなんですけどね。私もそう思います。

 
Neutron:


あなたの方法で試算して、結果を教えてください。

グラフで示した条件{N=120,q(mo)=60.91%/12 初期資本=100 }で、Kをいじるのは私の手に負えませんね。

この条件でのkOptを どなたか教えていただければ、丸めを考慮したpostnumerandを集計してみますが・・・。

;)

 

では、マテマット さんとソレント さんに質問です。上で、お二人は、「では、どうするか」という意味で、ユニークなミハイル・アンドレーエヴィチの 決断に言及されましたが、すべてが明らかになりましたね...。のように、次はどうする？

尊敬するMikhail Andreyevichは、スコアを2倍にする時間の短縮式しか持っていないことが判明しました、何もありません:-)一般的には、Alexeyからの kOptの 近似解を待つことになるのでしょう。

 
Neutron:

では、マテマットさんとソレントさんに質問です。上で、お二人は、「では、どうするか」という意味で、ユニークなミハイル・アンドレーエヴィチの 決断に言及されましたが、すべてが明らかになりましたね...。のように、次はどうする？

尊敬するMikhail Andreyevichは、スコアを2倍にする時間の短縮式しか持っていないことが判明しました、何もありません:-)というわけで、Alexeyからの kOptの 近似解を待つことにしましょう。

面白い結論ですね。

締め切りTopt 前に任意の（比例を含む）撤退を伴う戦略は、最適ではありません...。デポがトプトより長いと仮定して......もちろんです。

写真（数値）をご覧ください...

;)

 

少し違った（より複雑な）問題の解決に着手しているように思えます。

ここで思い出してほしいのは、私は時間 tの 間、現在の預金額の一定の利息qが 毎月発生する預金を使用しており、毎月q 以上0％以下の一定の利息kを 引き出さなければならないという規定である。それだけです。

私は、預金を考慮せずに期間tの 出金を最大化するような kOptを 見つけなければならない。この解は、2つのパラメータqと tの 関数として解析的に示されなければならない（数値解、あらゆる種類のグラフや依存関係の形の部分解は、すでに得られているので、興味がない）。解析解が近似解である場合、問題の解の宣言された精度が達成されるqと tの 限界を指定する必要があります。

追伸：インフレ、経過利子qの 非一定性、パラメータkの 変動など、あらゆる仕掛けは、最も単純なケースの解が得られるまで、考慮する意味がないと思います。

 

"慣習上、私は時間 tの 間、現在の預金額の一定割合qが 毎月発生する使用中の預金を持っており、私はq 以上0％以下の一定割合kを 毎月引き出さなければならないことを思い出してください。それだけです。"

.

セルゲイ そして、すでに答えは出ているのですが、あまり単純な式ではありませんが、かなり理解しやすいと思います。このような場合、参考書ではノモグラムという形で答えが示されているのが普通です。

問題の仕様から、「qは0.1<q<0.3の範囲にある」ことがわかる。

範囲 "時間 t " を指定する

 

Oleg, for Forextは 50に設定することができます。なぜなら、預金の特性寿命が 5年未満では、すべての利益を引き出すのが正しく、最初の預金額で「一生」の利息を提供する必要があるからです。5年以上経過している場合、初回入金額は問題なく、1000ルーブルから始められますが、最適な出金率が表示されます。さらに、特性寿命は実行の義務ではないことを考慮すれば（統計の話なので）、このパラメータを式から除外し、定数=50とすることができる。したがって、kOptについては、（理想的には）TCの平均熟練度-qという 1つのパラメータのみから解析的な近似値を得ることができるのです。

t<50の場合はkOpt=q

t>50の場合kOpt=F(q)

指定された条件下での解析的依存性F(q) の近似的な形が知りたいところである。

 

どうすれば数式がシンプルになるのか、まだわかりません。ニュートン法では、少なくとも3回目か4回目の反復から多かれ少なかれ厳密な解が得られます。非常に面倒な、多層式であることがわかります。

qを 明確にすることで、二項展開が役に立たないことがさらに確認された。q=0.1、t=10 であっても、二項展開の項を多く残す必要がある。そして、tと qが 大きければ大きいほど、悪いということになる。つまり、合理的なt（おそらく20以下ではない）であれば、ほとんどの場合

(1+q-k)^t ～ exp((q-k)t)

観測によると、qが 大きくtが 小さい場合（例えばそれぞれ0.3と10）、1ヶ月に稼いだ金額のほとんど（70%）を引き出すことが最適である。

小さなqと 小さなtでは、合理的な範囲に極端なものはなく、利益のすべてを引き出すことが必要である。

一方、qが 中程度、tが 中程度（0.2、20）では、収入の2分の1（44％）を引き出すことが合理的であることがわかる。

そして、qが 中程度でtが 大きい場合（0.2、30）には、収益の26％という少ない割合で引き出すのが合理的であることがわかります。

などなど。この問題は、パラメータが異なると、定性的には異なる挙動を示す。楽観的で単一の答えはないようだ。qと tに 依存するkの 推定値のようなものを作ってみたらどうだろう？

P.S.セルゲイ さんのコメント拝見しました。OK、t=50を 修正。問題はより簡単になった。利益のより少ない部分を取り出せばよいのである（q=0.1,t=50->k/q= 0.3, すなわち30%）。これは、可能な限り最大のk/q である。

 

αの最適値は、正の領域から負の領域への移行に対応する。

.

計算式は上で述べたとおりですが、ここで繰り返し述べます。

Matcadetで再現できる --- パラメータを素早く調整できる。

(とBは役割を果たさない）。

 
Mathemat:

qと tの 関数としてkを 推定してみたらどうだろう？


そうすると、解析解のエレガントさが失われてしまうのです。この場合、数値解法を用いるのがより正しい。単純な表現では手が届かない問題のようです...。

出金額の合計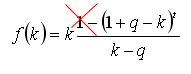 の元の式を簡略化してみた。

この場合、パラメータ kに関する 一次導関数の一般的な形式は、単純な二次方程式にまで大幅に簡略化される。

.

を解くことで、近似式を得ることができる。

t>50、q>0.1 の範囲で許容される精度を有する。

もっと欲しかった...。

1...121314151617181920212223242526...31
新しいコメント
理由: