賃借人 - ページ 16 1...91011121314151617181920212223...31 新しいコメント 削除済み 2011.02.26 07:34 #151 これらのパラメータが結果にどのような影響を与えるか、興味深いところです。 削除済み 2011.02.26 07:46 #152 例えば、ベースラインの条件下で、バルブ位置を変えてみると、次のような興味深い結果が得られます。 . . . それは大局的な判断のため...。 私たちは、最後の依存関係に興味があります (「a-da」位相プロファイル -- 最後のグラフはその特殊なケース) 削除済み 2011.02.26 08:12 #153 Mathemat: あまりうまくいかなかった。計算結果はここには書きません。美しいものは何もない。 1+q-k = 1+epsilon、epsilonは小さな値、という観測結果を利用してみました。そして、微分をk個ずつテイラー級数で展開し、まず3次までの項を小さく保持した。そして、簡略化した後、3次方程式を得た。3次の最小の項を捨てて、できた2次のものを解いてみた。失敗した:判別式が正になるのは、tが小さいときだけだ。 3乗の項を否定したのは間違いでした。εの3乗の項ではありますが、小さくはありません。epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3) のように持っていたのですが、どうでしょうか?tが大きいとかなり小さくなることがわかる(ε~0.01がかなり現実的な仮定であるとしても)。そして、人は立方体のものを解きたいとは思わない。 オレグが 何を手に入れるか見てみよう。 追伸:ε*t =O(1) (または q*t = O(1) )とすると、べき乗関数を指数で近似することができます。試してみよう。 Taylor級数を使わず、単純に接線法(Newtonだったと思います)で計算する方法もあります。そして、かなり厳密な解析解を得ることもできる。 ポイントは、最初は連続時間ではなく、格子関数--つまり、適切な変換がまず行われなければならない、という条件です。そうして初めて、小さなイプシロンの導入が有効になるのです。これらは、格子関数の特性です。 ところで、私が問題を解く最初のステップで扱ったのは、連続時間領域への変換で、鎖状離散--周波数--時間でのラプラス変換を用いたものでした。正確には、これも...。 削除済み 2011.02.26 08:24 #154 そこで、さらに分析の対象となるのは、関数 . Neutron 2011.02.26 09:08 #155 Mathemat:そして、キュービックのほうは解きたくないんです。アレクセイ、3次方程式の根の解析式は見たことがない(部分的に簡略化した場合を除く)。そんな表現はないのでしょうか?二次方程式のように、x1=b/2+SQRT()...と。など知っていたら投稿してください。インターネットで調べても出てこないんです。そういえば、根を調和関数で表すというのもありましたね。 Taylor級数を使わずに、単純に接線法(Newtonだったと思います)で行う方法もあります。そして、かなり厳密な解析解を得ることもできる。 この方法で本当に解析的に近似解を求めることができるのでしょうか?聞いたことないですね。非常に興味深い、メソッドの例を見てみたい。 スタジオへ行こう! そうですね、tが 大きい場合に得られる解の話ですね。これは「不殺生」預金の事例として実用的にも興味深い。何 tの 近似値を得ることができたのでしょうか?t->infの リミットトランジションが可能なのかもしれません。そうすると、最適なペイアウト率kを、たった一つのパラメータq(経過利子の値)の関数として、解析的に表すことができるかもしれません。これは素晴らしい結果でしょう。 avtomat: ポイントは、初期条件に連続時間ではなく、格子関数--つまり、まず変換が必要なことです。そうして初めて、小さなイプシロンの導入が有効になるのです。これらは、格子関数の特性です。ところで、私が問題を解く最初のステップで扱ったのは、連続時間領域への変換で、鎖状離散--周波数--時間でのラプラス変換を用いたものでした。正確には、これを含めて...です。Oleg さん、上で得られた導出可能な平均の和の解析式 が連続時間に対して限界ではないと思われるのはなぜでしょうか?結局、元の時系列(トピックの最初の投稿で書いた繰り返し形)の最小間隔(ステップ)の上限を規定しなかったのです。そうであれば、 dt->0での 極限遷移において、あるdf(t) があれば十分であり、 矛盾はないのだが......。 削除済み 2011.02.26 10:09 #156 Neutron: Oleg さん、上記の微分の和の解析式が連続時間の極限でないと思うのはなぜでしょう?結局、元の時系列の最小間隔(ステップ)の制限は特に規定しなかった(トピックの最初の投稿で反復された形の表記)。もしそうなら、 dt->0での 極限遷移では、定数df(t) があれば十分で、 矛盾はないのだが......。 そうではない...ここで小さなイプシロンを導入してみては...。 はい、特にどこにも定めていませんが、問題の文言自体が格子関数の使用を暗黙のうちに示唆しているのです。 つまり、マッチングは格子のノードで行われることになります。さらに、格子関数には中間点が存在せず、格子のノードのみが存在する。そのため、中間値を構成しようとすると、すべて誤った結果になる(ちなみに、この問題は信号の量子化の分野に属する)。中間値は、サンプリングレートを上げる、つまり、より多くのノードを持つ格子関数を再度導入することで構築できるが、現象の本質を根本的に変えることはないだろう。これは、特に、1次、2次などの差分に代えて、1次、2次などの微分を使用することを意味します。積分の代わりに -- 和を ...など-- これはひとつの研究分野です。 しかし、ある分野から別の分野へ、そしてまた別の分野へと移動する方法があるのです。 この問題の場合、この方法は私たちには合いません。そこで、まず離散時間から連続時間へ移行する必要があります。 Alexey Subbotin 2011.02.26 10:21 #157 avtomat: ポイントは、初期条件が連続時間ではなく、格子関数であること、つまり、まず変換を行う必要があることです。 ...を使うかどうかは別として、ラプラス変換の離散版、つまりZ変換の利用可能な装置を使う。もっとシンプルでいいと思いませんか? Ilnur Iksanov 2011.02.26 10:27 #158 Neutron: 3次方程式の根の解析式は見たことがない(部分的に簡略化したものは除く)。持ってないんですか?二次方程式のように、x1=b/2+SQRT()...と。など知っていたら投稿してください。インターネットで調べても出てこないんです。 カルダノの公式 学校の授業で、調和関数による根の表現もあることを思い出しました ヴィエッツの三角関数式 削除済み 2011.02.26 10:31 #159 alsu: ...あるいは、生成するのではなく、ラプラス変換の離散版、すなわちZ変換の利用可能な装置を使用することです。もっとシンプルでいいと思いませんか? 問題はそこではない。最初に「%growth - %yield - yield」という3次元の絵があり、すべてがすでに計算されており、それは離散的な領域にある。 あとは、それを分析的に表現することがスポーツの課題です;) Neutron 2011.02.26 14:02 #160 Ilnur: カルダノ式 ビエトの三角関数公式 Ilnur さん、ありがとうございます。 1...91011121314151617181920212223...31 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
これらのパラメータが結果にどのような影響を与えるか、興味深いところです。
例えば、ベースラインの条件下で、バルブ位置を変えてみると、次のような興味深い結果が得られます。
.
.
.
それは大局的な判断のため...。
私たちは、最後の依存関係に興味があります
(「a-da」位相プロファイル -- 最後のグラフはその特殊なケース)
あまりうまくいかなかった。計算結果はここには書きません。美しいものは何もない。
1+q-k = 1+epsilon、epsilonは小さな値、という観測結果を利用してみました。そして、微分をk個ずつテイラー級数で展開し、まず3次までの項を小さく保持した。そして、簡略化した後、3次方程式を得た。3次の最小の項を捨てて、できた2次のものを解いてみた。失敗した:判別式が正になるのは、tが小さいときだけだ。
3乗の項を否定したのは間違いでした。εの3乗の項ではありますが、小さくはありません。epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3) のように持っていたのですが、どうでしょうか?tが大きいとかなり小さくなることがわかる(ε~0.01がかなり現実的な仮定であるとしても)。そして、人は立方体のものを解きたいとは思わない。
オレグが 何を手に入れるか見てみよう。
追伸:ε*t =O(1) (または q*t = O(1) )とすると、べき乗関数を指数で近似することができます。試してみよう。
Taylor級数を使わず、単純に接線法(Newtonだったと思います)で計算する方法もあります。そして、かなり厳密な解析解を得ることもできる。
ポイントは、最初は連続時間ではなく、格子関数--つまり、適切な変換がまず行われなければならない、という条件です。そうして初めて、小さなイプシロンの導入が有効になるのです。これらは、格子関数の特性です。
ところで、私が問題を解く最初のステップで扱ったのは、連続時間領域への変換で、鎖状離散--周波数--時間でのラプラス変換を用いたものでした。正確には、これも...。
そこで、さらに分析の対象となるのは、関数
.
そして、キュービックのほうは解きたくないんです。
アレクセイ、3次方程式の根の解析式は見たことがない(部分的に簡略化した場合を除く)。そんな表現はないのでしょうか?二次方程式のように、x1=b/2+SQRT()...と。など知っていたら投稿してください。インターネットで調べても出てこないんです。そういえば、根を調和関数で表すというのもありましたね。
Taylor級数を使わずに、単純に接線法(Newtonだったと思います)で行う方法もあります。そして、かなり厳密な解析解を得ることもできる。
この方法で本当に解析的に近似解を求めることができるのでしょうか?聞いたことないですね。非常に興味深い、メソッドの例を見てみたい。
スタジオへ行こう!
そうですね、tが 大きい場合に得られる解の話ですね。これは「不殺生」預金の事例として実用的にも興味深い。何 tの 近似値を得ることができたのでしょうか?t->infの リミットトランジションが可能なのかもしれません。そうすると、最適なペイアウト率kを、たった一つのパラメータq(経過利子の値)の関数として、解析的に表すことができるかもしれません。これは素晴らしい結果でしょう。
avtomat:
ポイントは、初期条件に連続時間ではなく、格子関数--つまり、まず変換が必要なことです。そうして初めて、小さなイプシロンの導入が有効になるのです。これらは、格子関数の特性です。
ところで、私が問題を解く最初のステップで扱ったのは、連続時間領域への変換で、鎖状離散--周波数--時間でのラプラス変換を用いたものでした。正確には、これを含めて...です。
Oleg さん、上で得られた導出可能な平均の和の解析式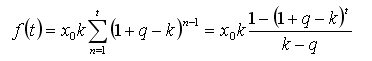 が連続時間に対して限界ではないと思われるのはなぜでしょうか?結局、元の時系列(トピックの最初の投稿で書いた繰り返し形)の最小間隔(ステップ)の上限を規定しなかったのです。そうであれば、 dt->0での 極限遷移において、あるdf(t) があれば十分であり、 矛盾はないのだが......。
が連続時間に対して限界ではないと思われるのはなぜでしょうか?結局、元の時系列(トピックの最初の投稿で書いた繰り返し形)の最小間隔(ステップ)の上限を規定しなかったのです。そうであれば、 dt->0での 極限遷移において、あるdf(t) があれば十分であり、 矛盾はないのだが......。
Oleg さん、上記の微分の和の解析式が連続時間の極限でないと思うのはなぜでしょう?結局、元の時系列の最小間隔(ステップ)の制限は特に規定しなかった(トピックの最初の投稿で反復された形の表記)。もしそうなら、 dt->0での 極限遷移では、定数df(t) があれば十分で、 矛盾はないのだが......。
そうではない...ここで小さなイプシロンを導入してみては...。
はい、特にどこにも定めていませんが、問題の文言自体が格子関数の使用を暗黙のうちに示唆しているのです。
つまり、マッチングは格子のノードで行われることになります。さらに、格子関数には中間点が存在せず、格子のノードのみが存在する。そのため、中間値を構成しようとすると、すべて誤った結果になる(ちなみに、この問題は信号の量子化の分野に属する)。中間値は、サンプリングレートを上げる、つまり、より多くのノードを持つ格子関数を再度導入することで構築できるが、現象の本質を根本的に変えることはないだろう。これは、特に、1次、2次などの差分に代えて、1次、2次などの微分を使用することを意味します。積分の代わりに -- 和を ...など-- これはひとつの研究分野です。
しかし、ある分野から別の分野へ、そしてまた別の分野へと移動する方法があるのです。
この問題の場合、この方法は私たちには合いません。そこで、まず離散時間から連続時間へ移行する必要があります。
ポイントは、初期条件が連続時間ではなく、格子関数であること、つまり、まず変換を行う必要があることです。
3次方程式の根の解析式は見たことがない(部分的に簡略化したものは除く)。持ってないんですか?二次方程式のように、x1=b/2+SQRT()...と。など知っていたら投稿してください。インターネットで調べても出てこないんです。
カルダノの公式
学校の授業で、調和関数による根の表現もあることを思い出しました
ヴィエッツの三角関数式
...あるいは、生成するのではなく、ラプラス変換の離散版、すなわちZ変換の利用可能な装置を使用することです。もっとシンプルでいいと思いませんか?
問題はそこではない。最初に「%growth - %yield - yield」という3次元の絵があり、すべてがすでに計算されており、それは離散的な領域にある。
あとは、それを分析的に表現することがスポーツの課題です;)
カルダノ式
ビエトの三角関数公式