- L'apprendimento automatico nel trading: teoria, modelli, pratica e algo-trading
- Filtri digitali adattivi
- Qualcosa di interessante nel video finanziario ottobre 2013
L'indicatore i-regr può fare regressioni polinomiali arbitrarie di qualsiasi grado. Non ho mai tentato nulla di più alto del 3° grado, ma il codice è lì per voi da guardare. Il 6° grado probabilmente ucciderà la vostra CPU, ma potete fare un tentativo.
L'indicatore i-regr può fare regressioni polinomiali arbitrarie di qualsiasi grado. Non ho mai tentato nulla di più alto del 3° grado, ma il codice è lì per voi da guardare. Il 6° grado probabilmente ucciderà la vostra CPU, ma potete fare un tentativo.
Grazie rocketman! Non ha ucciso affatto la mia CPU - lavorerò con questo per un po' usando e vedrò cosa mi viene in mente.
Aggiornamento:
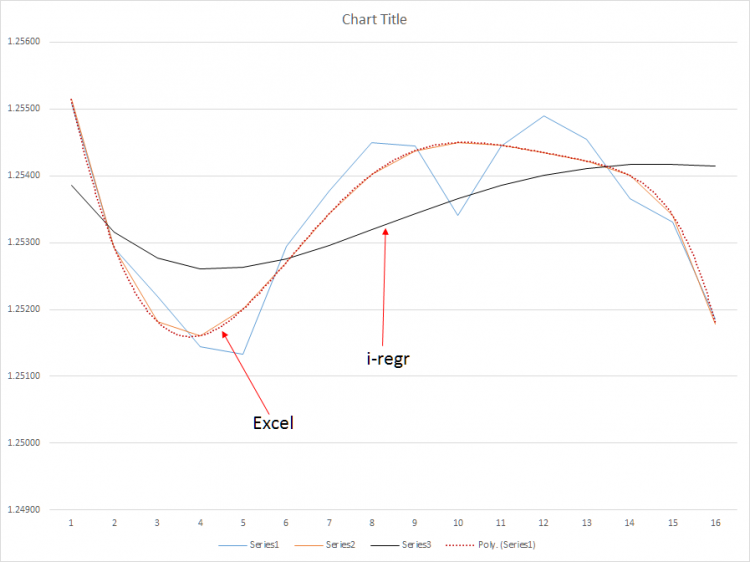
i-regr non sembra avere un alto grado di precisione - potrebbe essere forse dovuto al metodo gauss (i-regr) e ai minimi quadrati (excel) usati per risolvere. Non lo so - sto ancora cercando, qualcuno ha qualche procedura poly migliore?
i-regr sta lavorando sul valore Close[] di ogni barra, il che probabilmente fa la differenza (immagino che tu abbia equalizzato le lunghezze dei pattern in MT4 ed excel).
Puoi cambiare questo facilmente cambiando Close[] in Open/High/Low o in qualsiasi altra espressione analitica, per esempio la funzione peso.
Tuttavia non credo che tu possa trarre profitto da questo, è proprio come qualsiasi altro indicatore di tendenza di riverniciatura.
Ciao dennisj2,
sei sicuro di aver davvero bisogno della tua formula?
Potresti provare prima a cercare altri filtri come Kalman, Ehlers, Gauss, Jurik (JMA), DEMA. La maggior parte di loro deriva dai filtri di frequenza passa-basso (fisici) e la maggior parte di loro ha trovato la sua strada nel codice di mt4.
Forse un JMA (ci sono molte varianti) con un periodo più lungo fa quello che stai cercando?
Ora inizia la mia ricerca.
Ora che ho identificato un'applicazione pratica, ho cercato di imparare (o, nel mio caso, di re-imparare) la matematica dietro la formula della linea di tendenza poli. Buona fortuna. La riduzione dei minimi quadrati e le matrici aggiunte alla formula estremamente complessa e ai calcoli dei coefficienti necessari introdotti dall'equazione polinomiale sono troppo difficili (per me) da tradurre in codice. Così, ho pensato che sarebbe stato più semplice chiamare Excel (molto probabilmente da c++), fornire un array di valori di dati (x,y), calcolare l'intercetta polinomiale (x,y) (valore della linea di tendenza) usando LINEST(), e restituire questo valore alla mia applicazione desktop (un'applicazione software proprietaria chiusa con funzionalità di chiamata limitata).
Assemblare la formula usando LINEST() è diventato un ostacolo sostanziale. È abbastanza facile fornire i dati - ma, come posso calcolare le intercette (x,y) mostrate così perfettamente sul grafico? Ogni nuova misura cambia la formula e usa nuovi coefficienti calcolati? Perché succede questo? Ho passato ore e ore (e anche di più) a cercare soluzioni su internet - e (proprio come un uomo) ho deciso finalmente di chiedere indicazioni.
Ho i valori sorgente (anni e anni di valori). Quello che mi manca è a) il metodo per generare l'intercetta poly(x,y), b) chiamando Excel esternamente per c) restituire la poly(x,y) basata sui dati (x,y) forniti -
Se qualcuno ha un articolo o un trattamento molto specifico di questo argomento, o anche disposto a dare una mano, sarei per sempre in debito.
dj
Ci sono un sacco di articoli sull'algebra con esempi in greco, ma in realtà si tratta di voodoo.
Per esempio c'è un articolo di wikipedia sulla regressione lineare che non ha alcun senso per me, eppure potrei codificare una versione di regressione lineare della tua linea proprio ora perché da qualche altra parte ho imparato a usare la formula
y=a+bx
Eppure da nessuna parte nell'articolo di wikipedia è menzionata questa formula, come può avere senso?
Inoltre ho imparato che quando si usa quella formula
a == pendenza
b = intercetta
la matematica per calcolare la pendenza e l'intercetta è nota ed è una procedura piuttosto semplice di calcolare le somme dei valori, squadrare alcuni di essi ecc.
So anche che la formula per una regressione quadratica (2° grado) è y=ax^2 + bx + c
Quindi penso che siano collegati, il che dovrebbe significare che l'equazione per la regressione di 3° grado è
y=ax^3 + bx^2 + cx + d
quindi penso che la regressione di 6° grado sarebbe
y=ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g
ma se a è la pendenza e b è l'intercetta cos'è c e quale sarebbe d ecc? Questo è l'unico motivo per cui non ho potuto codificare la tua linea, non so quali siano i coefficienti o come calcolarli.
AGGIORNAMENTO: ok ho imparato qualcos'altro che mi confonde ora.
in un altro articolo il polinomio quadratico è descritto come
ax^2 + bx + c = 0
Questo significa che non abbiamo bisogno di conoscere la matematica per l'intercetta della pendenza e potremmo risolvere la quadratica per trovare i valori di a, b e c?
Ma come fa ax^2 + bx + c = 0
in relazione a
y=ax^2 + bx + c ?
Sembrano simili ma come mai una è y= e l'altra è =0?
DSC,
la pendenza in un punto può essere calcolata dalla prima derivazione di una funzione.
Una funzione lineare come y=ax+b ha in qualsiasi punto la stessa pendenza: a.
In generale la derivazione di una funzione lineare ax^n + bx^n-1 + ... + z = y è semplicemente: nax^(n-1) + (n-1)bx^n-2 .. = y' - l'ultima costante della funzione originale diventa 0, sempre!
Quindi ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )e la funzione quadratica diventa y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 ).
Ma penso che per capire l'idea dei filtri sia meglio pensare (e leggere) alle frequenze di filtraggio. Non importa se si tratta di suoni o immagini o citazioni o ..
Si vuole sempre sbarazzarsi del rumore - in generale - delle frequenze a breve termine. E l'uso di funzioni lineari è solo un approccio.
Grazie per aver cercato di spiegarmelo, ma non so perché quelle equazioni significano quello che significano. Se so come calcolare i coefficienti singolarmente in modo procedurale posso usarli e inserire i valori, ma questo è tutto.
Capisco il concetto di filtri, ero solo interessato a capire come codificare la linea dell'OP.
Ma per quanto riguarda il farlo, quando dici,
"Quindi ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )e la funzione quadratica diventa y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 )."
Non ho idea di cosa tu stia parlando o anche di come questo sia rilevante, quindi probabilmente non farò alcuna codifica di linee di poli in qualsiasi momento presto lol
SDC:
Ci sono un sacco di articoli là fuori sull'algebra con esempi in greco, ma in realtà è voodoo.
SDC - ora sei allo stesso livello di me - la formula di regressione lineare che ho trovato funziona - e ci sono due formule nettamente diverse che ho trovato che producono risultati identici. Queste formule sono ottime se la regressione lineare (una linea di tendenza dritta) è quello che stavamo cercando.
Prima, un po' di materiale di riferimento:
Microsoft: http://office.microsoft.com/en-us/excel-help/linest-HP005209155.aspx
IntegralCalc: https://www.youtube.com/watch?v=1pawL_5QYxE&noredirect=1
Data l'equazione di regressione lineare y = mx + b:
Dove y = prezzo, (ad esempio, Close[x])
e x = indice (ad esempio, Bar[x])
e m = Pendenza (il coefficiente applicato ad ogni coppia (x,y))
e b = Intercetta Y (il valore base dell'intercetta Y applicato ad ogni coppia (x,y))
Metodo A: Da IntegralCalcMetodo B: Da Microsoft (dove x(overbar) e y(overbar) sono mezzi)
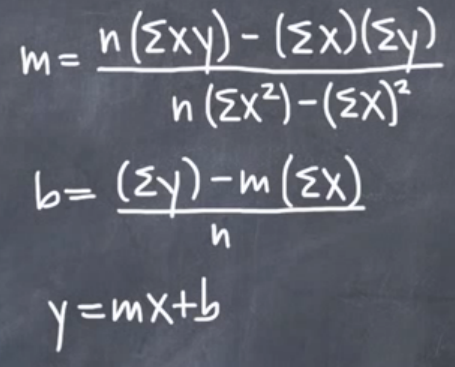
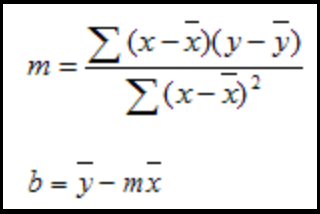
Anche la formula della linea di tendenza della regressione polinomiale all'ennesimo grado è relativamente facile da applicare:
Data la formula: y = m1*x1 + m2*x2 + m3*x3 + ... + b
Dove le variabili x, y, m e b portano la stessa definizione descritta nell'equazione lineare.
Sembra che io abbia tutto, quindi cosa manca?
Quello che manca è il calcolo della m (pendenza) e della b (intercetta Y) per una regressione polinomiale; l'equazione lineare per calcolare questi valori non si applica a una regressione polinomiale. Da quello che ho imparato, la regressione polinomiale richiede una formula che calcola i minimi quadrati basati su un sistema di equazioni polinomiali usando una matrice. Guardate i grafici di esempio qui sopra. Nel primo grafico, le linee polinomiali (6) sono assolutamente immacolate - i massimi e i minimi sono chiaramente indicati. Con questi dati, sarò in grado di tenere i trade più a lungo di quanto non faccia oggi, raddoppiando, potenzialmente triplicando i miei pip medi per trade.
Nel secondo grafico, mostro i risultati del metodo poly(6) vs. il metodo i-regr che usa una matrice gauss per risolvere i coefficienti di pendenza - e, inutile dirlo, è abbastanza inutile a causa della latenza sostanziale del metodo. D'altra parte, una semplice media mobile è ancora peggio - la SMA è troppo sensibile durante le correzioni di mercato intermedie che potrebbero causare una reazione eccessiva del mio EA.
Sono disposto a pagare qualcuno per sviluppare un vero indicatore di regressione polinomiale - ma, i risultati devono assolutamente rispecchiare i risultati che Excel produce. La funzione LINEST() è una scatola nera dove viene usato molto voodoo per calcolare i coefficienti. Molto semplicemente, ho bisogno di capire questo voodoo.
Aggiornamento: ho allegato un file che mostra il metodo implementato in Excel.
i-regr sta lavorando sul valore Close[] di ogni barra, il che probabilmente fa la differenza (immagino che tu abbia equalizzato le lunghezze dei pattern in MT4 ed excel).
Puoi cambiare questo facilmente cambiando Close[] in Open/High/Low o in qualsiasi altra espressione analitica, per esempio la funzione peso.
Tuttavia non credo che si possa trarre un profitto da questo, è proprio come qualsiasi altro indicatore di tendenza di riverniciatura.
Grazi -
Ho usato l'i-regr e confrontato i risultati di cui sopra - l'algoritmo Poly(6) contro l'i-regr mostra che l'i-regr ha una latenza sostanzialmente maggiore del poly(6) sulla base dello stesso set di dati - la latenza è la morte in questo mercato. I miei EA non fanno trading sulle oscillazioni intraday ma piuttosto, tengono per il trend. Quindi, ti sbagli - io traggo profitto dai miei EA e, con un indicatore reattivo più lento, i miei EA cattureranno più mercato di quanto non facciano oggi. In particolare, quando avrò integrato un vero algoritmo poly(6), avrò la possibilità di tenere le posizioni aperte più a lungo e di prevedere i cambiamenti di tendenza 3-4 periodi prima, migliorando i miei punti di ingresso.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso