В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
Il n'y a pas de contradiction ici. La loi fondamentale de l'offre et de la demande prédit ces effets. Le problème est que l'ensemble du modèle doit être considéré de manière dynamique, c'est-à-dire que les limites du canal fondamental horizontal changent avec le temps. Pour comprendre ce dont je parle, il faut d'abord considérer un modèle statique classique de l'offre et de la demande (pour "ici et maintenant") :
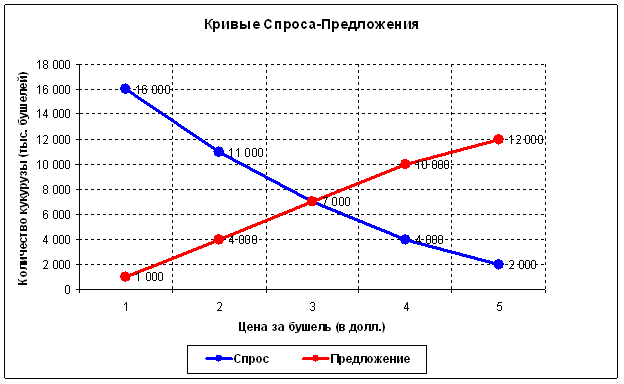
C'est-à-dire qu'à chaque instant, il n'y a qu'un seul point d'échange maximalement efficace d'un bien (dans ce cas, 7 000 boisseaux à un prix de 3 $). À tous les autres points, moins de biens seront échangés contre moins d'argent. La situation macroéconomique change constamment, ce qui signifie que ce point d'échange efficace change également. Cependant, le marché est efficace et sa tâche principale consiste à rechercher en permanence ce point ou le prix d' équilibre ("tous ceux qui voulaient acheter ont acheté, tous ceux qui voulaient vendre ont vendu"). Le volume à ce point doit être important, car c'est à ce moment-là que la quantité maximale de marchandises est échangée. Il faut du temps pour que le marché réalise un tel volume. Cette théorie prédit l'effet de l'accumulation des volumes :
Le marché est la plupart du temps en phase de consolidation (dans la zone de son efficacité maximale).
Cependant, l'économie mondiale dans son ensemble est en constante évolution. De nouvelles technologies apparaissent, les niveaux de vie s'améliorent. Par conséquent, d'une part, de plus en plus de biens et de services sont nécessaires et, d'autre part, les progrès scientifiques et technologiques permettent de produire de plus en plus de biens et de services. La liquidité augmente avec le temps. Le volume des marchés mondiaux doit augmenter et, par conséquent, leur volatilité s'accroît, ce qui entraîne l'effondrement de la taille des crises. La demande augmentant avec le temps, le prix augmente. Dans le même temps, le progrès scientifique et technologique fournit à cette demande de plus en plus de biens et de services. Par conséquent, le point d'équilibre se déplace généralement vers le haut et vers la droite au fil du temps. Le marché, qui oscille constamment autour de ce point, croît généralement lui aussi (tendance à des prix élevés).

C'est de là que vient cet "effet de tendance". Tout cela s'ajoute si bien aux calculs mathématiques que c'en est tout simplement époustouflant. En tout état de cause, ce sont les effets économiques qui devraient expliquer les dépendances mathématiques, et non l'inverse.
Il y a une inexactitude dans l'article, si nous prenons un marin ivre comme analogie, alors la taille du pas est différente. En gros, un pas fait 80 cm de long si l'on part du pub, et un pas en arrière (vers le pub) fait 60 cm. La tendance est la même, il est également connu que le mouvement à la baisse du marché est plus rapide que le mouvement à la hausse. Et dans l'article, tous les pas sont identiques +1 ou -1.
Ce modèle ne peut donc pas être considéré comme adéquat. Il s'agit simplement d'une pièce de monnaie, dont les propriétés de distribution sont connues et étudiées depuis longtemps.
Il y a une inexactitude dans l'article, si nous prenons le marin ivre comme analogie, alors la taille de la marche est différente. En gros, un pas fait 80 cm de long si l'on s'éloigne du pub, et un pas en arrière (vers le pub) fait 60 cm. La tendance est la même, il est également connu que le mouvement à la baisse du marché est plus rapide que le mouvement à la hausse. Et dans l'article, tous les pas sont identiques +1 ou -1".
La pièce a un analogue continu - le modèle du mouvement brownien géométrique. Il est décrit ici à l'adresse http://algoritmus.ru/?p=2889.
"Approche stochastique de la résolution des problèmes de trading algorithmique".
Auteurs : Arsen Yakovlev, Grigory Franguridi
Publié : magazine "D-Shtrich" #16/6 septembre 2010
Cet article reprend les mêmes idées que le mien, mais avec plus de mathématiques. Le choix d'un modèle discret ou continu est une question de goût. Ils sont identiques. Seul un modèle comporte des intégrales et l'autre des sommes. Et le modèle à pièces est déjà compris par les écoliers, alors que le modèle continu n'est compris que par les étudiants.
"Il est également connu que le mouvement à la baisse du marché est plus rapide que le mouvement à la hausse" - c'est très intéressant pour moi - pouvez-vous me donner un lien vers la recherche/l'article - j'en ai besoin pour mon auto-éducation.
"Ce modèle ne peut donc en aucun cas être considéré comme adéquat. Il s'agit simplement d'une pièce de monnaie dont les propriétés de distribution sont connues et étudiées depuis longtemps." - Aucun modèle ne décrit correctement la réalité à 100 %. Y compris le taux de la pièce de monnaie en tant que modèle de marché. C'est pourquoi nous avons dû inventer un modèle de pièce avec une tendance pour être plus adéquat au marché.
- 2010.09.13
- val
- algoritmus.ru
Pourquoi une pièce de monnaie ? Elle a deux faces - que reflètent-elles ? Seulement un mouvement aléatoire idéal sur une ligne droite (analogue - haut, bas), c'est-à-dire unidimensionnel. Le prix peut avoir un autre état - plat, c'est-à-dire qu'il s'agit déjà d'une pièce de monnaie à trois faces, c'est-à-dire que nous avons une marche aléatoire bidimensionnelle. Les graphiques ci-dessus montrent qu'un tel état du marché n'est pratiquement pas modélisé - il n'y a pas de plat absolu.
La courbe jaune de la figure 2 est celle qui se rapproche le plus d'un plat. L'aplat le plus serré sera obtenu si nous prenons le paramètre a=-0,5. Nous obtiendrons alors une ligne horizontale +1 -1 +1 -1 -1 +1 -1 -1 ..... Les deux côtés d'une pièce de monnaie suffisent donc à décrire un plat. D'ailleurs, dans l'article, "plat" s'appelle "anti-tendance".
Mais l'ensemble du graphique deviendra alors plus horizontal, si je comprends bien, et sur le marché réel, il peut y avoir à la fois une tendance marquée et un plat dur, c'est-à-dire que ces phénomènes sont indépendants. L'indépendance est la nécessité d'un troisième côté de la pièce. Simplement, le marché erre sur le plan, parce que le facteur temps erre, et la pièce a un modèle unidimensionnel d'errance, et un simple (sans errance) balayage de ce modèle pour le temps n'est pas tout à fait correct. Mais malgré cela, cet article est très utile.
Exactement, dans le modèle de la pièce avec une tendance, la tendance est considérée comme constante sur toute la durée de vie du marché. Or, comme le montre l'indicateur de tendance du taux réel, la tendance change constamment. Et ce n'est qu'en moyenne sur une longue période de temps (années) que la tendance est mesurée comme une constante.
Pour que le modèle "taux de la pièce avec tendance" corresponde au marché, vous pouvez le compliquer. Le paramètre "a" peut être rendu chaotiquement dépendant du temps ou quelque chose d'autre peut être inventé. C'est une question de créativité. Strictement parlant, il n'est pas nécessaire d'introduire une deuxième dimension, mais si vous le souhaitez, vous pouvez ajouter un deuxième multiplicateur chaotique à côté de "a".
Un modèle simple à tendance constante est nécessaire pour tester, par exemple, cet indicateur New Moving Mini-Max d'analyse technique et son implémentation dans MQL5. Il n'est pas réaliste de traiter un tel indicateur sur le cours réel, mais ce serait bien de le tester sur un modèle simple à tendance constante.
...Le choix d'un modèle discret ou continu est une question de goût. Ils sont identiques. Seul un modèle comporte des intégrales et l'autre des sommes. Et le modèle à pièces est déjà compris par les écoliers, et le modèle continu seulement par les étudiants...
c'est là qu'est l'erreur.
1. le passage du modèle continu au modèle discret doit se faire correctement.
2. les deux modèles peuvent être identiques (continu et discret), mais il faut remplir la condition, le pas en + et en - doit être le même. Sa magnitude.
3. a pris des barres pour analyser, que votre affirmation serait vraie "Ils sont les mêmes". Seulement un modèle a des intégrales et l'autre des sommes" Prouvez que toutes les barres sont identiques. Pouvez-vous le prouver ?
4. un seul graphique a cette propriété, le graphique renko... vous pouvez le remplacer par +1 -1(https://www.mql5.com/fr/code/9447#25419).
Merci pour le lien vers l'article. Je l'ai lu. Il suggère d'utiliser le modèle ARFIMA, vous marchez au hasard. Il s'agit de modèles différents. Il serait intéressant de lire l'article suivant, à la fois le vôtre et celui de l'auteur. Il y est prouvé que les modèles de marché que vous proposez sont adéquats. Pas seulement affirmés en paroles, mais prouvés mathématiquement... et le calcul de ce chiffre ...
H.Y. Beaucoup de gens comprennent ce beau mot d'adéquation, mais ne savent même pas comment le calculer. Vous avez écrit dans votre post que le modèle adéquat à 100% n'existe pas. Je suis tout à fait d'accord avec vous. La question est de savoir dans quelle mesure le modèle proposé est adapté au marché par 20, 30 ou 99,999999999%....
Essayez de modéliser une pile, la pile a une structure claire, la pile reçoit des ordres pour un certain nombre de points vers le haut et vers le bas.
Le générateur passe par toutes les cellules (il peut ne pas s'agir de +1 -1 mais de la génération de volumes aléatoires), puis une fois que toutes les cellules de la pile sont passées par le générateur, le calcul de l'endroit où déplacer le point central de la pile est effectué.
Et n'oubliez pas de redémarrer SRAND après avoir généré 32768 rand, sinon votre séquence sera répétée.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article Marche Aléatoire et l’Indicateur de Tendance a été publié :
Marche Aléatoire ressemble beaucoup aux données réelles du marché, mais elle présente des caractéristiques importantes. Dans cet article, nous examinerons les propriétés de Marche Aléatoire, simulées à l’aide du jeu de lancer de pièces. Pour étudier les propriétés des données, l’indicateur de tendance est élaboré.
Pour commencer, simulons le résultat d’un jeu de lancer de pièces, en utilisant un générateur de nombres aléatoires. Donc, que les têtes soient un +,1 et les queues soient -1. Le résultat du i-ième lancer de la pièce est x (i) = p (1/2), où p (1/2) est une fonction, en prenant les valeurs +1 avec la probabilité de 1/2 et la valeur -1, avec la même probabilité 1/2.
Ensuite, la Marche Aléatoire https://en.wikipedia.org/wiki/Random_walk sera simplement la somme de x (i). Pour plus de simplicité, nous partons de zéro.
Figure 1. Marche aléatoire: (axe vertical - position actuelle sur la ligne, par l’axe horizontal - intervalles de temps)
Auteur : Гребенев Вячеслав