Fourier extrapolation of price - indicateur pour MetaTrader 5

Un modèle trigonométrique multi-harmonique (ou multi-tons) d'une série de prix x[i], i=1..n, est donné par :

où :

• x[i] - prix passé à la i-ième barre, total n prix passés ;
• m - biais ;
• a[h] et b[h] - coefficients d'échelle des harmoniques ;
• w[h] - fréquence d'une harmonique ;
• h - nombre d'harmoniques ;
• H - nombre total d'harmoniques ajustées.

L'ajustement de ce modèle consiste à trouver m, a[h], b[h] et w[h] pour que les valeurs modélisées soient proches des valeurs réelles. La recherche des fréquences harmoniques w[h] est la partie la plus difficile de l'ajustement d'un modèle trigonométrique. Dans le cas d'une série de Fourier, ces fréquences sont fixées à 2*pi*h/n. Mais l'extrapolation de la série de Fourier consiste simplement à répéter les n prix passés dans le futur.

Cet indicateur utilise l'algorithme de Quinn-Fernandes pour trouver les fréquences harmoniques. Il ajuste les harmoniques de la série trigonométrique une par une jusqu'à ce que le nombre total d'harmoniques H spécifié soit atteint. Après avoir ajusté une nouvelle harmonique, l'algorithme codé calcule le résidu entre le modèle mis à jour et les valeurs réelles et ajuste une nouvelle harmonique au résidu.

L'indicateur a les paramètres d'entrée suivants :

• Npast - nombre de barres passées, auxquelles la série trigonométrique est ajustée ;
• Nfut - nombre de barres futures prédites ;
• Nharm - nombre total d'harmoniques dans le modèle ;
• FreqTOL - tolérance des calculs de fréquence.
  

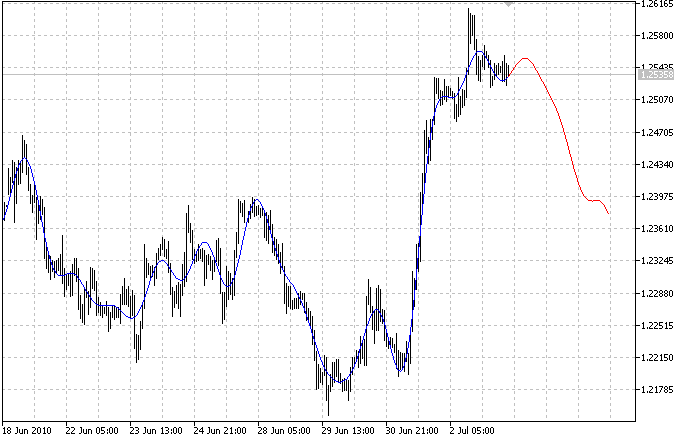
L'indicateur trace deux courbes : la courbe bleue indique les valeurs passées modélisées et la courbe rouge indique les valeurs futures modélisées.