거래 로봇을 무료로 다운로드 하는 법을 시청해보세요
당사를 Twitter에서 찾아주십시오!
당사 팬 페이지에 가입하십시오
당사 팬 페이지에 가입하십시오
스크립트가 마음에 드시나요? MetaTrader 5 터미널에서 시도해보십시오
가격 시리즈 x[i], i=1..n의 다중 조화(또는 다중 톤) 삼각 모델은 다음과 같이 주어집니다:
x[i] = m + Sum( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
여기서
- x[i] - i번째 막대의 과거 가격, 총 n개의 과거 가격;
- m - 바이어스;
- a[h] 및 b[h] - 고조파의 스케일링 계수;
- w[h] - 고조파의 주파수;
- h - 고조파 수
- H - 피팅된 고조파의 총 개수.
이 모델을 맞추는 것은 모델링된 값을 실제 값에 가깝게 만드는 m, a[h], b[h], w[h]를 찾는 것을 의미합니다. 고조파 주파수 w[h]를 구하는 것은 삼각 모델 피팅에서 가장 어려운 부분입니다. 푸리에 급수의 경우 이러한 주파수는 2*pi*h/n으로 설정됩니다. 그러나 푸리에 급수 외삽은 단순히 과거의 가격 n을 미래로 반복하는 것을 의미합니다.
이 인디케이터는 퀸-페르난데스 알고리즘을 사용해 고조파 주파수를 찾습니다. 지정된 총 고조파 수 H에 도달할 때까지 삼각급수의 고조파를 하나씩 맞추는 방식입니다. 새 고조파를 맞춘 후 코딩된 알고리즘은 업데이트된 모델과 실제 값 사이의 잔차를 계산하고 그 잔차에 새 고조파를 맞춥니다.
인디케이터에는 다음과 같은 입력 매개변수가 있습니다:
- Npast - 삼각급수가 맞는 과거 막대의 수입니다;
- Nfut - 예상되는 미래 막대의 수입니다;
- Nharm - 모델의 총 고조파 수입니다;
- FreqTOL - 주파수 계산의 허용 오차.
표시기는 두 개의 곡선을 표시합니다. 파란색 곡선은 모델링된 과거 값을 나타내고 빨간색 곡선은 모델링된 미래 값을 나타냅니다.
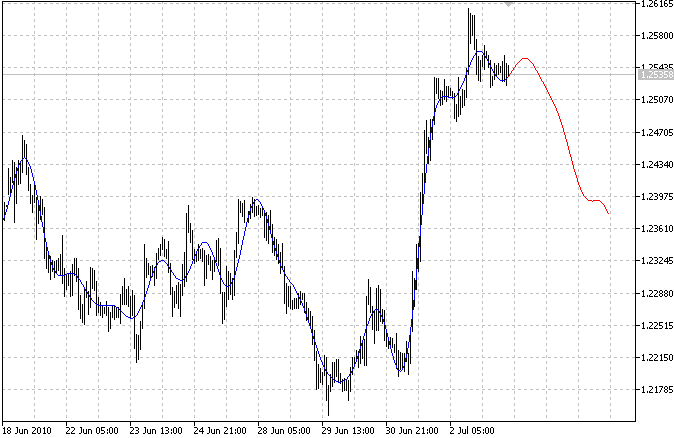
MetaQuotes Ltd에서 영어로 번역함.
원본 코드: https://www.mql5.com/en/code/130
 AR extrapolation of price
AR extrapolation of price
이 지표는 자동 회귀 모델을 사용하여 가격을 추정합니다.
 Linear regression slope
Linear regression slope
선형 회귀 기울기를 SMA로 정규화합니다.
