Discusión sobre el artículo "Distribuciones Estadísticas en MQL5: tomando lo mejor de R" - página 19

[Aleksey Nikolayev]

Aleksey Nikolayev:
Se desea añadir la distribución de Kolmogorov a la biblioteca. Es muy útil por su uso en el criterio de Kolmogorov-Smirnov y en el problema de la búsqueda de la descomposición de un proceso aleatorio.

La dejaré aquí por si acaso. Cálculo de la FCD y sus complementos para la distribución del estadístico de Kolmogorov-Smirnov para la prueba unilateral de una muestra.

[Aleksey Nikolayev]

¿Alguien lo ha utilizado?

[Renat Fatkhullin]

Aleksey Nikolayev:

La CDF de la distribución hipergeométrica se calcula incorrectamente mediante la función MathCumulativeDistributionHypergeometric(). Por definición, la función de distribución de probabilidad debe definirse para cualquier número real. A continuación se muestra un script en mql5 con sus resultados y, para comparar, lo mismo en R.

resultado:

-1.0 nan 2

0.0 0.0 0

0,5 nan 2

división por cero en 'Hypergeometric.mqh' (241,35)

Resultado:

[1] 0.0000000 0.0000000 0.0000000 0.2222222

Ha pasado argumentos incorrectos y ha obtenido ERR_ARGUMENTS_INVALID (2). Estamos comprobando los parámetros de entrada con más detalle, y parece que R ha sustituido la respuesta por ceros.

//+------------------------------------------------------------------+
//| Función de distribución acumulativa hipergeométrica (CDF) | |
//+------------------------------------------------------------------+
//| La función devuelve la probabilidad de que una observación |
//| de la distribución Hipergeométrica con parámetros m,n,k |
//| es menor o igual que x.|
//||
//| Argumentos:|
//| x : El número deseado de objetos |
//| m : Tamaño de la población
//| k : Número de elementos con la característica deseada |
//|| en la población|
//| n : Número de muestras extraídas |
//| cola : Bandera para calcular la cola inferior |
//| log_mode : Modo logaritmo, si es true calcula valores logarítmicos.
//| error_code : Variable para el código de error |
//||
//| Valor de retorno:|
//| El valor de la función de distribución acumulativa hipergeométrica.
//| con parámetros m,n,k, evaluados en x. |||
//+------------------------------------------------------------------+
//| Basado en el algoritmo de John Burkardt.|
//+------------------------------------------------------------------+
double MathCumulativeDistributionHypergeometric(const double x,const double m,const double k,const double n,const bool tail,const bool log_mode,int &error_code)
  {
//--- comprobar NaN
   if(!MathIsValidNumber(x) || !MathIsValidNumber(m) || !MathIsValidNumber(k) || !MathIsValidNumber(n))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- m,k,n,x deben ser enteros
   if(m!=MathRound(m) || k!=MathRound(k) || n!=MathRound(n) || x!=MathRound(x))
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- m,k,n,x debe ser positivo
   if(m<0 || k<0 || n<0 || x<0)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }
//--- comprobar rangos
   if(n>m || k>m)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

[Renat Fatkhullin]

Aleksey Nikolayev:

Por ejemplo, algunos coeficientes binomiales (no todos) son negativos:

resultado: -309196571788882235

debería ser: 349615716557887488

Debido a la gran K (28) el long de 64 bits se desbordó allí. El valor de retorno es long.

Para contar valores dentro de esos límites, es necesario reescribir la función a valores dobles.

[Aleksey Nikolayev]

Renat Fatkhullin:

Pasaste argumentos incorrectos y obtuviste ERR_ARGUMENTS_INVALID (2). Comprobamos los parámetros de entrada con más detalle, y R parece haber sustituido la respuesta por ceros.

1) Cualquier CDF - función de distribución de probabilidad (¡las discretas no son una excepción!) DEBE DEFINITIVAMENTE estar definida para todos los números reales. A continuación se muestra un análogo del código en R con su resultado, mostrando cómo esto debería contar en la realidad. Por cierto, tienes algunas funciones CDF discretas contando correctamente y otras no.

2) Para el valor 1 se obtiene un error de división por cero.

[Renat Fatkhullin]

Aleksey Nikolayev:

1) Cualquier CDF - función de distribución de probabilidad (¡las discretas no son una excepción!) DEBE DEFINITIVAMENTE definirse para todos los números reales. A continuación se muestra un análogo del código en R con su resultado que muestra cómo esto debe ser considerado en la realidad. Por cierto, algunas funciones CDF discretas las has contado correctamente y otras no.

2) Para el valor 1 obtienes un error de división por cero.

Lee el código de la función y su comprobación, está en el código fuente.

No tengo R a mano, tengo que comprobarlo por separado. Veo división por cero, hay que entender las condiciones de contorno.

[Aleksey Nikolayev]

Renat Fatkhullin:

Debido a una K grande (28), el long de 64 bits se desbordó allí. El valor de retorno es long.

Para contar valores dentro de esos límites, debe reescribir la función a valores dobles.

Está claro. Es sólo que hay un error con el logaritmo del coeficiente binomial en argumentos enteros y pensé que esa era la razón. Ahora he mirado el código y me he dado cuenta de que estaba equivocado: la razón es otra.

#include <Math\Stat\Math.mqh>

void OnStart()
  { Print(MathBinomialCoefficientLog(62,28));
    Print(MathBinomialCoefficientLog(62.0,28.0));
  }

resultado:

test_clog (EURUSD.m,MN1) -nan(ind)

test_clog (EURUSD.m,MN1) 40.39561099351077

PS Incorrecto, el problema también está en el desbordamiento

[Aleksey Nikolayev]

Renat Fatkhullin:

No hay R a mano,

R en línea

[Denis Kirichenko]

Algunos problemas con NoncentralBeta. Tomé el script de la Documentación.

Estos son los resultados para diferentes parámetros.

[Denis Kirichenko]

Fórmula en Documentación:

Es el análogo en Wikipedia:

Mirado el código.

La función MathRandomNoncentralBeta() tiene líneas como esta:

//--- generar número aleatorio usando ChiCuadrado No Central
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomNoncentralChiSquare(b2,lambda2,error_code);
result[i]=chi1/(chi1+chi2);

La misma Wikipedia tiene esto:

The noncentral beta distribution (Type I) is the distribution of the ratio

donde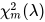 es unavariable aleatoria chi-cuadrado no centralcon grados de libertad m y parámetro de no centralidad 𝜆 , y 𝜒 𝑛 2 es unavariable aleatoria chi-cuadrado centralcon grados de libertad n , independiente de 𝜒 𝑚 2 ( 𝜆 ) .

Es decir, se toman dos variables aleatorias, donde la primera es de una distribución chi-cuadrado no central y la segunda es de una central. Probablemente el código pueda corregirse en este sentido:

//--- generar número aleatorio usando ChiCuadrado No Central
double chi1=MathRandomNoncentralChiSquare(a2,lambda2,error_code);
double chi2=MathRandomChiSquare(b2,error_code);
result[i]=chi1/(chi1+chi2);

Los gráficos modificados del ejemplo serán los siguientes.