- Filtros digitales adaptativos
- Preguntas de los principiantes MQL5 MT5 MetaTrader 5
- Aprendizaje automático en el trading: teoría, práctica, operaciones y más
El indicador i-regr puede hacer regresiones polinómicas arbitrarias de cualquier grado. Nunca he intentado nada más alto que el 3er grado, pero el código está ahí para que lo veas. El 6º grado probablemente matará tu CPU, pero puedes intentarlo.
El indicador i-regr puede hacer regresiones polinómicas arbitrarias de cualquier grado. Nunca he intentado nada más alto que el 3er grado, pero el código está ahí para que lo veas. El 6º grado probablemente matará tu CPU, pero puedes intentarlo.
¡Gracias rocketman! No mató a mi CPU en absoluto - Voy a trabajar con esto por un tiempo usando y ver lo que me sale.
Actualizar:
i-regr no parece tener un alto grado de precisión - podría ser posiblemente debido a la gauss (i-regr) y los cuadrados mínimos (Excel) método utilizado para resolver. No sé - sigue buscando, ¿alguien tiene algún procedimiento poli mejor?
i-regr está trabajando en el valor de Close[] de cada barra, lo que probablemente hace la diferencia (supongo que usted ha igualado las longitudes de los patrones en MT4 y excel).
puedes cambiar esto fácilmente cambiando Close[] por Open/High/Low o por cualquier otra expresión analítica, por ejemplo, la función de peso.
sin embargo no creo que puedas obtener beneficios de esto, es como cualquier otro indicador de tendencia repintado.
Hola dennisj2,
¿estás seguro de que realmente necesitas tu fórmula?
Tal vez intente primero buscar otros filtros como Kalman, Ehlers, Gauss, Jurik (JMA), DEMA. La mayoría de ellos se derivan de los filtros de frecuencia de paso bajo (físicos) y la mayoría de ellos han encontrado su camino en el código mt4.
¿Puede ser que un JMA (hay muchas variaciones) con un período más largo haga lo que usted está buscando?
Ahora comienza mi búsqueda.
Ahora que identifiqué una aplicación práctica, busqué aprender (o, en mi caso, reaprender) la matemática detrás de la fórmula de la línea de tendencia poli. Buena suerte con eso. La reducción de mínimos cuadrados y las matrices añadidas a la fórmula extremadamente compleja y los cálculos de coeficientes requeridos introducidos por la ecuación polinómica son demasiado difíciles (para mí) de traducir en código. Así que pensé que sería más fácil llamar a Excel (probablemente desde c++), suministrar una matriz de valores de datos (x,y), calcular el intercepto polinómico (x,y) (valor de la línea de tendencia) usando LINEST(), y devolver este valor a mi aplicación de escritorio (una aplicación de software propietario cerrada con funcionalidad de llamada limitada).
El montaje de la fórmula utilizando LINEST() se ha convertido en un obstáculo importante. Es bastante fácil suministrar los datos, pero, ¿cómo puedo calcular los interceptos (x,y) que se muestran tan perfectamente en el gráfico? ¿Cada nueva medida cambia la fórmula y utiliza nuevos coeficientes calculados? ¿Por qué ocurre esto? He pasado horas y horas (y algunas más) buscando soluciones en Internet, y (como un hombre) he decidido finalmente pedir indicaciones.
Tengo los valores de origen (años y años). Lo que me falta es a) el método para generar la intercepción poly(x,y), b) llamar a Excel externamente para c) devolver el poly(x,y) basado en los datos (x,y) suministrados -
Si alguien tiene un artículo o tratamiento muy específico de este tema, o incluso está dispuesto a echar una mano, estaría eternamente en deuda.
dj
Hay un montón de artículos por ahí sobre el álgebra con ejemplos en griego, pero realmente es vudú.
Por ejemplo, hay un artículo de la wikipedia sobre la regresión lineal que no tiene ningún sentido para mí, sin embargo, podría codificar una versión de regresión lineal de su línea ahora mismo porque en otro lugar aprendí a usar la fórmula
y=a+bx
Sin embargo, en ninguna parte del artículo de la wikipedia se menciona esa fórmula, ¿cómo puede tener sentido?
también aprendí al usar esa fórmula
a == pendiente
b== intercepción
la matemática para calcular la pendiente y el intercepto es conocida y es un procedimiento bastante simple de calcular las sumas de los valores, elevar al cuadrado algunos de ellos, etc.
También sé que la fórmula para una regresión cuadrática (2º grado) es y=ax^2 + bx + c
Así que estoy pensando que están relacionados, lo que debería significar que la ecuación para la regresión de 3er grado es
y=ax^3 + bx^2 + cx + d
así que creo que la regresión de 6º grado sería
y=ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g
pero si a es la pendiente y b es el intercepto, ¿qué es c y qué sería d, etc.? Esa es la única razón por la que no pude codificar tu línea, no sé cuáles son los coeficientes ni cómo calcularlos.
ACTUALIZACIÓN: ok he aprendido algo más que me confunde ahora.
en otro artículo se describe el polinomio cuadrático como
ax^2 + bx + c = 0
¿Significa eso que no necesitamos saber la matemática de la pendiente e intercepción y que podemos resolver la cuadrática para encontrar los valores de a, b y c?
¿Pero cómo se relaciona ax^2 + bx + c = 0
se relaciona con
y=ax^2 + bx + c ?
Se parecen pero ¿cómo es que una es y= y la otra es =0?
COSUDE,
la pendiente en un punto puede ser calculada por la primera derivación de una función.
Una función lineal como y=ax+b tiene en cualquier punto la misma pendiente: a.
En general la derivación de una función lineal ax^n + bx^n-1 + ... + z = y es simplemente: nax^(n-1) + (n-1)bx^n-2 .. = y' - la última constante de la función original se convierte en 0, ¡siempre!
Así que ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )y la función cuadrática se convierte en y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 ).
Pero creo que para entender la idea de los filtros es mejor pensar (y leer) sobre las frecuencias de filtrado. No importa si se trata de sonido o imágenes o citas o .
Uno siempre quiere deshacerse del ruido - en general - las frecuencias más corto plazo. Y el uso de funciones lineales es sólo un enfoque.
Gracias por intentar explicarme eso pero no sé por qué esas ecuaciones significan lo que significan. Si sé cómo calcular los coeficientes individualmente de forma procedimental puedo usarlos y enchufar los valores pero eso es todo.
Sí entiendo el concepto de los filtros, sólo me interesaba saber cómo codificar la línea del OP.
Pero con respecto a hacer eso, cuando dices,
"Así que ax + b = y => y' = a ( <= 1*a^(1-1); b=0 )y la función cuadrática se convierte en y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 )."
No tengo ni idea de lo que estás hablando o incluso cómo eso es relevante, así que probablemente no voy a hacer ninguna codificación de la línea poli en cualquier momento lol
SDC:
Hay un montón de artículos por ahí sobre el álgebra con ejemplos en griego, pero realmente es vudú.
SDC - usted está ahora en el mismo nivel que yo - la fórmula de regresión lineal que encontré funciona - y hay dos fórmulas claramente diferentes que encontré que producen resultados idénticos. Estas fórmulas son grandes si la regresión lineal (una línea de tendencia recta) es lo que estábamos buscando.
Primero, algo de material de referencia:
Microsoft: http://office.microsoft.com/en-us/excel-help/linest-HP005209155.aspx
IntegralCalc: https: //www.youtube.com/watch?v=1pawL_5QYxE&noredirect=1
Dada la ecuación de regresión lineal y = mx + b:
Donde y = precio, (por ejemplo, Close[x])
y x = índice (por ejemplo, Bar[x])
y m = Pendiente (el coeficiente aplicado a cada par (x,y))
y b = Intercepción Y (el valor base de la intercepción Y aplicado a cada par (x,y))
Método A: Desde IntegralCalcMétodo B: Desde Microsoft (donde x(overbar) e y(overbar) son medias)
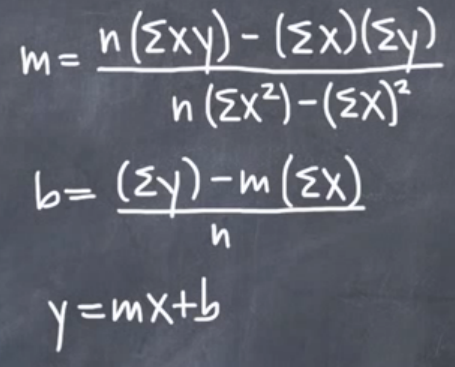
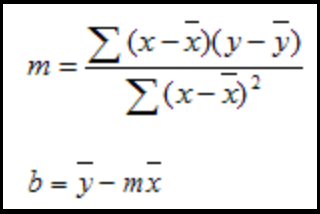
Incluso la fórmula de la línea de tendencia de regresión polinómica a la enésima potencia es relativamente fácil de aplicar:
Dada la fórmula: y = m1*x1 + m2*x2 + m3*x3 + ... + b
Donde las variables x, y, m y b llevan la misma definición descrita en la ecuación lineal.
Parece que lo tengo todo, ¿qué falta?
Lo que falta es el cálculo de la m (pendiente) y la b (intersección Y) para una regresión polinómica; la ecuación lineal para calcular estos valores no se aplica a una regresión polinómica. Por lo que he aprendido, la regresión polinómica requiere una fórmula que calcula los mínimos cuadrados basada en un sistema de ecuaciones polinómicas utilizando una matriz. Mira los gráficos de ejemplo de arriba. En el primer gráfico, las líneas polinómicas(6) son absolutamente inmaculadas: los máximos y los mínimos están claramente definidos. Con estos datos, seré capaz de mantener las operaciones más tiempo de lo que lo hago hoy en día, duplicando y potencialmente triplicando mi promedio de pips por operación.
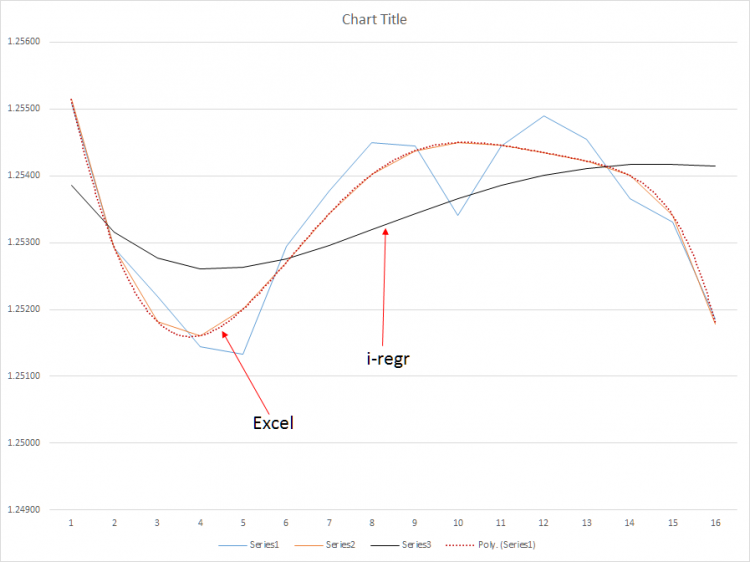
En el segundo gráfico, muestro los resultados del método poly(6) frente al método i-regr que utiliza una matriz de gauss para resolver los coeficientes de pendiente - y, no hace falta decir, es bastante inútil debido a la latencia sustancial del método. Por otra parte, una media móvil simple es aún peor - el SMA es demasiado sensible durante las correcciones intermedias del mercado que podrían causar una reacción excesiva de mi EA.
Estoy dispuesto a pagar a alguien para desarrollar un verdadero indicador de regresión polinómica - pero, los resultados deben reflejar absolutamente los resultados que produce Excel. La función LINEST() es una caja negra en la que se utiliza mucho vudú para calcular los coeficientes. Simplemente, necesito entender este vudú.
Actualización: He adjuntado un archivo que muestra el método implementado en Excel.
i-regr está trabajando en el valor de Close[] de cada barra, lo que probablemente hace la diferencia (supongo que usted ha igualado las longitudes de los patrones en MT4 y excel).
Puedes cambiar esto fácilmente cambiando Close[] por Open/High/Low o por cualquier otra expresión analítica, por ejemplo, la función de peso.
Sin embargo, no creo que se pueda obtener un beneficio de esto, es como cualquier otro indicador de tendencia de repintado.
Grazi -
Usé el i-regr y comparé los resultados anteriores - el algoritmo Poly(6) vs. i-regr muestra que el i-regr tiene una latencia sustancialmente mayor que el poly(6) basado en el mismo conjunto de datos - la latencia es la muerte en este mercado. Mis EAs no operan con la oscilación intradía, sino que mantienen la tendencia. Por lo tanto, usted está equivocado - yo me beneficio de mis EAs y, con un indicador reactivo más lento, mis EAs capturarán más del mercado de lo que lo hacen hoy. Específicamente, una vez que haya integrado un verdadero algoritmo poly(6), tendré la capacidad de mantener las posiciones abiertas por más tiempo y predecir los cambios de tendencia 3-4 períodos antes, mejorando mis puntos de entrada.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso