Discusión sobre el artículo "Neuroredes profundas (Parte V). Optimización bayesiana de los hiperparámetros de las DNN"
He experimentado con BayesianOptimisation.
Tenías el mayor conjunto de 9 parámetros optimizables. Y usted dijo que se necesita mucho tiempo para calcular
Probé un conjunto de 20 parámetros a optimizar con 10 primeros conjuntos aleatorios. Tardé 1,5 horas en calcular las combinaciones en BayesianOptimisation, sin tener en cuenta el tiempo de cálculo del propio NS (sustituí el NS por una simple fórmula matemática para el experimento).
Y si quieres optimizar 50 o 100 parámetros, probablemente tardarás 24 horas en calcular 1 conjunto. Creo que sería más rápido generar docenas de combinaciones aleatorias y calcularlas en NS y luego seleccionar las mejores por Precisión.
En la discusión del paquete se habla de este problema. Hace un año, el autor escribió que si encuentra un paquete más rápido para los cálculos, lo usará, pero por ahora - como está. Allí dieron un par de enlaces a otros paquetes con optimización bayesiana, pero no está claro cómo aplicarlos para un problema similar, en los ejemplos se resuelven otros problemas.
bigGp - no encuentra el conjunto de datos SN2011fe para el ejemplo (aparentemente fue descargado de Internet, y la página no está disponible). No pude probar el ejemplo. Y de acuerdo con la descripción - algunas matrices adicionales son necesarios.
laGP - alguna fórmula confusa en la función de fitness, y hace cientos de sus llamadas, y cientos de cálculos NS son inaceptables en términos de tiempo.
kofnGA - puede buscar sólo X mejor de N. Por ejemplo 10 de 100. Es decir, no optimiza un conjunto de todos los 100.
Los algoritmos genéticos tampoco son adecuados, porque también generan cientos de llamadas a la función de aptitud (cálculos NS).
En general, no hay ningún análogo, y la propia BayesianOptimisation es demasiado larga.
He experimentado con BayesianOptimisation.
Tenías el mayor conjunto de 9 parámetros optimizables. Y usted dijo que tomó mucho tiempo para calcular
Probé un conjunto de 20 parámetros a optimizar con 10 primeros conjuntos aleatorios. Tardé 1,5 horas en calcular las propias combinaciones en BayesianOptimisation, sin tener en cuenta el tiempo de cálculo del propio NS (sustituí el NS por una simple fórmula matemática para el experimento).
Y si quieres optimizar 50 o 100 parámetros, probablemente tardarás 24 horas en calcular 1 conjunto. Creo que sería más rápido generar docenas de combinaciones aleatorias y calcularlas en NS, y luego seleccionar las mejores por Precisión.
En la discusión del paquete se habla de este problema. Hace un año el autor escribió que si encuentra un paquete más rápido para los cálculos, lo usará, pero por ahora - como está. Allí dieron un par de enlaces a otros paquetes con optimización bayesiana, pero no está claro cómo aplicarlos para un problema similar, en los ejemplos se resuelven otros problemas.
bigGp - no encuentra el conjunto de datos SN2011fe para el ejemplo (aparentemente fue descargado de Internet, y la página no está disponible). No pude probar el ejemplo. Y de acuerdo con la descripción - algunas matrices adicionales son necesarios.
laGP - alguna fórmula confusa en la función de fitness, y hace cientos de sus llamadas, y cientos de cálculos NS son inaceptables en términos de tiempo.
kofnGA - puede buscar sólo X mejor de N. Por ejemplo 10 de 100. Es decir, no optimiza un conjunto de todos los 100.
Los algoritmos genéticos tampoco son adecuados, porque también generan cientos de llamadas a la función de aptitud (cálculos NS).
En general, no existe un análogo, y la propia BayesianOptimisation es demasiado larga.
Existe un problema. Está relacionado con el hecho de que el paquete está escrito en R puro. Pero las ventajas de utilizarlo para mí personalmente superan los costes de tiempo. Hay un paquete hyperopt (Python)/ No he tenido la oportunidad de probarlo, y es viejo.
Pero creo que alguien reescribirá el paquete en C++. Por supuesto, usted puede hacerlo usted mismo, transferir algunos de los cálculos a la GPU, pero tomará mucho tiempo. Sólo si estoy realmente desesperado.
Por ahora usaré lo que tengo.
Suerte
También experimenté con ejemplos del propio paquete GPfit.
He aquí un ejemplo de optimización de 1 parámetro que describe una curva con 2 vértices (el GPfit f-ya tiene más vértices, yo dejé 2):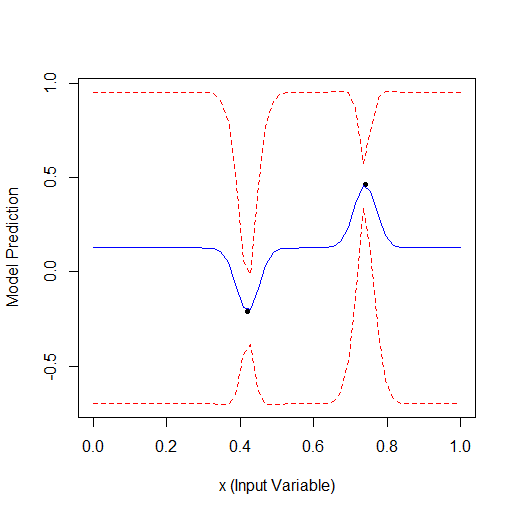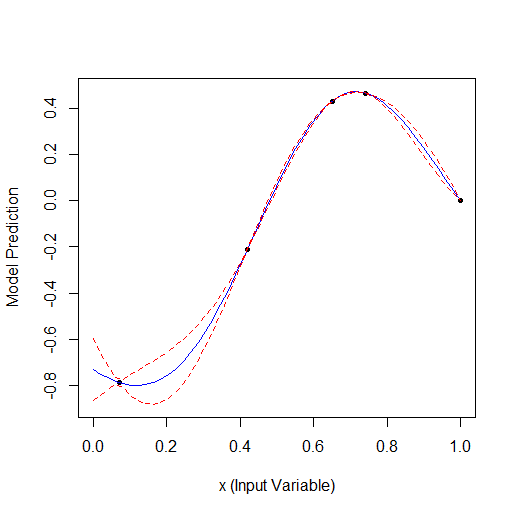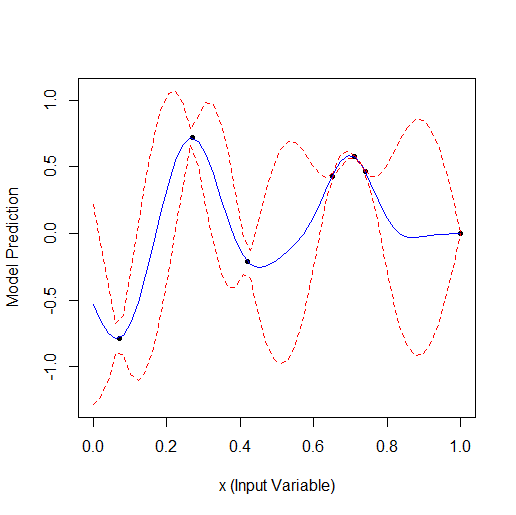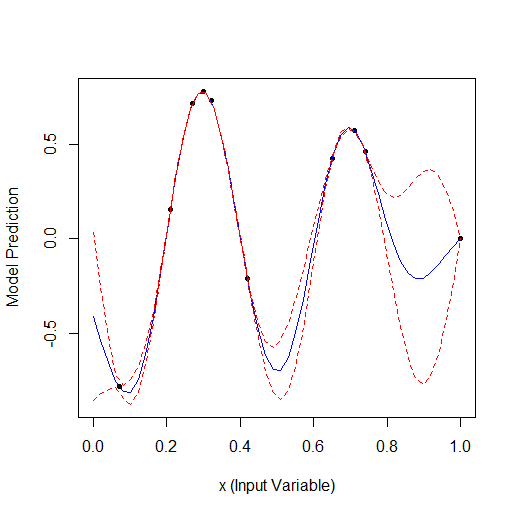
Tomando 2 puntos al azar y luego optimizando. Se puede ver que encuentra primero el vértice pequeño y luego el más grande. Total 9 cálculos - 2 aleatorios y + 7 en la optimización.
Otro ejemplo en 2D - optimizando 2 parámetros. La f-y original tiene este aspecto: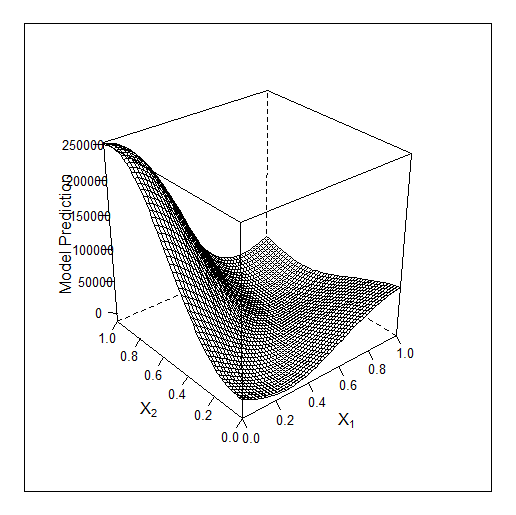
Optimización a 19 puntos:

Total 2 puntos aleatorios + 17 encontrados por el optimizador.
Comparando estos 2 ejemplos podemos ver que el número de iteraciones necesarias para encontrar el máximo al añadir 1 parámetro se duplica. Para 1 parámetro el máximo se encontró para 9 puntos calculados, para 2 parámetros para 19.
Es decir, si se optimizan 10 parámetros, pueden necesitarse 9 * 2^10 = 9000 cálculos.
Aunque en 14 puntos el algoritmo casi encontró el máximo, esto es aproximadamente 1,5 veces el número de cálculos. entonces 9 * 1,5:10 = 518 cálculos. También mucho, para un tiempo de cálculo aceptable.
Los resultados obtenidos en el artículo para 20 - 30 puntos pueden estar lejos del máximo real.
Creo que los algoritmos genéticos incluso con estos ejemplos sencillos necesitarán muchos más puntos para calcular. Así que probablemente no hay mejor opción.
También experimenté con ejemplos del propio paquete GPfit.
He aquí un ejemplo de optimización de 1 parámetro que describe una curva con 2 vértices (el GPfit f-ya tiene más vértices, yo dejé 2):
Tomando 2 puntos al azar y luego optimizando. Se puede ver que encuentra primero el vértice pequeño y luego el más grande. Total 9 cálculos - 2 aleatorios y + 7 en la optimización.
Otro ejemplo en 2D - optimizando 2 parámetros. El f-ya original tiene este aspecto:
Optimiza hasta 19 puntos:
Total 2 puntos aleatorios + 17 encontrados por el optimizador.
Comparando estos 2 ejemplos podemos ver que el número de iteraciones necesarias para encontrar el máximo al añadir 1 parámetro se duplica. Para 1 parámetro el máximo se encontró para 9 puntos calculados, para 2 parámetros para 19.
Es decir, si optimizas 10 parámetros, puedes necesitar 9 * 2^10 = 9000 cálculos.
Aunque en 14 puntos el algoritmo casi encontró el máximo, esto es aproximadamente 1,5 veces el número de cálculos. entonces 9 * 1,5:10 = 518 cálculos. También mucho, para un tiempo de cálculo aceptable.
1. Los resultados obtenidos en el artículo para 20 - 30 puntos pueden estar lejos del máximo real.
Creo que los algoritmos genéticos incluso con estos ejemplos sencillos necesitarán calcular muchos más puntos. Así que creo que no hay mejor opción después de todo.
Bravo.
Está claro.
Hay varias conferencias en YouTube que explican cómo funciona la optimización bayesiana. Si no lo has visto, te sugiero que lo veas. Es muy informativo.
¿Cómo insertó la animación?
Intento utilizar métodos bayesianos siempre que es posible. Los resultados son muy buenos.
1. Hago una optimización secuencial. Primero - inicialización de 10 puntos aleatorios, cálculo de 10-20 puntos, después - inicialización de 10 mejores resultados de la optimización anterior, cálculo de 10-20 puntos. Normalmente, después de la segunda iteración, los resultados no mejoran significativamente.
Suerte
En YouTube hay una serie de conferencias que explican cómo funciona la optimización bayesiana. Si no las ha visto, le aconsejo que las vea. Es muy informativo.
He mirado el código y el resultado en forma de imágenes (y te lo he enseñado). Lo más importante es el Proceso Gaussiano de GPfit. Y la optimización es la más habitual - sólo tiene que utilizar el optimizador de la entrega estándar de R y buscar el máximo en la curva / forma que GPfit salió con 2, 3, etc puntos. Y lo que ha salido se puede ver en las imágenes animadas de arriba. El optimizador sólo intenta sacar los 100 mejores puntos aleatorios.
Tal vez voy a ver conferencias en el futuro, cuando tengo tiempo, pero por ahora sólo voy a utilizar GPfit como una caja negra.
¿Cómo insertaste la animación?
Sólo mostré el resultado paso a paso GPfit::plot.GP(GP, surf_check = TRUE), lo pegué en Photoshop y lo guardé allí como un GIF animado.
siguiente - inicialización de los 10 mejores resultados de la optimización anterior, los cálculos de 10-20 puntos.
Según mis experimentos, es mejor dejar todos los puntos conocidos para futuros cálculos, porque si se eliminan los inferiores, GPfit puede pensar que hay puntos interesantes y querrá calcularlos, es decir, habrá repetidas ejecuciones del cálculo NS. Y con estos puntos inferiores, GPfit sabrá que no hay nada que buscar en estas regiones inferiores.
Aunque si los resultados no mejoran mucho, significa que hay una extensa meseta con pequeñas fluctuaciones.
Como instalar y lanzar ?
).

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
Pruebas a futuro de los modelos con parámetros óptimos
Comprobemos en cuánto tiempo los parámetros óptimos de DNN producirán resultados con una calidad aceptable para las pruebas de valores "futuros" de las cotizaciones. La prueba se realizará en el entorno restante tras las optimizaciones y pruebas anteriores de la siguiente forma.
Utilizar una ventana móvil de 1350 barras, entrenar = 1000, probar = 350 (para la validación - las primeras 250 muestras, para la prueba - las últimas 100 muestras) con paso 100 para recorrer los datos después de las primeras (4000 + 100) barras utilizadas para el preentrenamiento. Realice 10 pasos "hacia adelante". En cada paso, dos modelos serán entrenados y probados:
- uno - utilizando el DNN preentrenado, es decir, realizar un ajuste fino en un nuevo rango en cada paso;
- el segundo, entrenando adicionalmente la DNN.opt, obtenida tras la optimización en la fase de ajuste fino, en un nuevo intervalo.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Realice la primera parte de la prueba hacia adelante utilizando el DNN preentrenado y los hiperparámetros óptimos, obtenidos de la variante de entrenamiento SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
La segunda etapa de la prueba hacia adelante utilizandoDnn.opt obtenido durante la optimización:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Comparar los resultados de la prueba, colocándolos en una tabla:
env$Score3_dnn env$Score3_dnnOpt
| iter | Puntuación3_dnn | Puntuación3_dnnOpt |
|---|---|---|
| Precisión Recall F1 | Precisión Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
La tabla muestra que los dos primeros pasos producen buenos resultados. En realidad, la calidad es la misma en los dos primeros pasos de ambas variantes, y después desciende. Por lo tanto, se puede suponer que después de la optimización y la prueba, la DNN mantendrá la calidad de la clasificación al nivel del conjunto de prueba en al menos 200-250 barras siguientes.
Existen muchas otras combinaciones para el entrenamiento adicional de los modelos en las pruebas de avance mencionadas en elartículo anterior y numerosos hiperparámetros ajustables.
Hola, ¿cuál es la pregunta?
Hola Vladimir,
No entiendo muy bien por qué tu NS se entrena con datos de entrenamiento y su evaluación se hace con datos de prueba (si no me equivoco lo utilizas como validación).
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
En este caso, ¿no obtendrás un ajuste al gráfico de prueba, es decir, elegirás el modelo que mejor funcionó en el gráfico de prueba?
También hay que tener en cuenta que la parcela de prueba es bastante pequeña y es posible que se ajuste a una de las regularidades temporales, que puede dejar de funcionar muy rápidamente.
Tal vez sea mejor estimar sobre la parcela de entrenamiento, o sobre la suma de parcelas, o como en Darch, (con los datos de validación presentados) sobre Err = (ErrLeran * 0.37 + ErrValid * 0.63) - estos coeficientes son por defecto, pero se pueden cambiar.
Hay muchas opciones y no está claro cuál es la mejor. Tus argumentos a favor del gráfico de prueba son interesantes.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Neuroredes profundas (Parte V). Optimización bayesiana de los hiperparámetros de las DNN:
En el artículo se analizan las posibilidades de la optimización bayesiana de los hiperparámetros de las neuroredes profundas obtenidas con diferentes formas de entrenamiento. Se compara la calidad de la clasificación de las DNN con los hiperparámetros óptimos en diferentes variedades de entrenamiento. Se ha comprobado mediante forward tests la profundidad de la efectividad de los hiperparámetros óptimos de la DNN. Se han definido los posibles campos de mejora de la calidad de la clasificación.
El resultado es bueno. Vamos a ver el gráfico de la historia de entrenamiento:
plot(env$Res1$Dnn.opt, type = "class")Fig.2 Historia de entrenamiento de la DNN con la variante SRBM + RP
Como podemos ver por la figura, el error en el conjunto de validación es inferior al error en el conjunto de entrenamiento. Esto indica que nuestro modelo no ha sido sobreentrenado y tiene una buena capacidad de generalización. La línea roja vertical muestra los resultados del modelo reconocido como el mejor, que hemos obtenido tras el entrenamiento.
Autor: Vladimir Perervenko