Discusión sobre el artículo "Modelo de Regresión Universal para la Predicción de Precio de Mercado" - página 8
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Contacte por mensaje privado, infórmese de las condiciones.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
¿Los indicadores son de pago o algo así? Publicado en la base de código, ¡úsalo a tu antojo!
Se publica un nuevo artículo Modelo de regresión universal para la predicción de precios de mercado:
Autor: Юсуфходжа
buen artículo.
muy impresionante
Es una pena, pero hay errores al principio del artículo.
En primer lugar, el incremento del precio en algún momento t tendrá, por supuesto, algún valor y lo denotamos por D0. Supongamos.
A continuación... Ahora en t=0, entiendo que no hay impacto en el precio y aparentemente tampoco hay incremento de precio por el impacto externo. Sin embargo, volvemos a llamar al delta D0.
Entonces ponemos dt/tau en la fórmula, que de todas formas es 1/C^2, es decir, le damos aceleración al impacto, que de todas formas moverá la regresión geométrica ¿Por qué deberíamos hacerlo? Después de todo, todavía no hemos definido - lo que este impacto es tal ...
bueno, en general.
Es una pena, pero hay errores al principio del artículo.
En primer lugar, el incremento del precio en algún momento t tendrá, por supuesto, algún valor y lo denotamos por D0. Supongamos.
A continuación... Ahora en t=0, entiendo que no hay impacto en el precio y aparentemente tampoco hay incremento de precio por el impacto externo. Sin embargo, volvemos a llamar al delta D0.
Entonces ponemos dt/tau en la fórmula, que de todas formas es 1/C^2, es decir, le damos aceleración al impacto, que de todas formas moverá la regresión geométrica ¿Por qué deberíamos hacerlo? Después de todo, todavía no hemos definido - lo que este impacto es tal ...
bueno, en general...
1. Do no es el incremento del precio, sino el potencial inicial de la fuerza que afecta al precio en el momento t=0.
2. del artículo: ".... supongamos que el precio de mercado, que está en equilibrio, sólo puede cambiar bajo la acción de alguna fuerza externa D(t), cuya magnitud y valor mediremos en la misma dimensión que el precio.
Supongamos también que el cambio en el precio de mercado P(t) con el paso del tiempo t desde el comienzo de la influencia de esta fuerza, aumentando continuamente desde el valor cero por alguna regularidad que aún desconocemos, tiende a alcanzar el valor P(∞) = D0 en el infinito. Es decir, por D0 entendemos un incremento o decremento finito del precio de mercado, dependiendo de la naturaleza y signo de esta fuerza influyente.
Además, suponemos que D(t=0) = D0. Supongamos además que durante el período infinitesimal de tiempo dt la fuerza influyente disminuirá en el valor dD(t) en proporción a la fuerza restante D(t) en el momento del tiempo t:
de donde obtenemos la dependencia exponencial de D(t) con el tiempo t en la forma:
Donde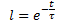
t - tiempo transcurrido desde el inicio del impacto de la fuerza desestabilizadora en unidades de la serie temporal, seg. (min, horas, días, semanas, décadas, meses, años);
τ (tau) - el coeficiente de proporcionalidad, numéricamente igual a la constante de tiempo del proceso, seg.(min, horas, días, semanas, décadas, meses, años)."
¿De dónde has sacado la dimensionalidad de 1/s^2? Ese cociente no tiene dimensionalidad. No lo colé, hipoteticé que, la tasa de cambio (disminución ) de una fuerza que actúa sobre un proceso es proporcional a la propia fuerza, lo cual no contradice la lógica, y luego, esta hipótesis se confirmó plenamente. Como coeficiente de proporcionalidad e introdujo la relación a (alfa) = 1/tau, que tiene la inversa del tiempo, dimensión. Por a (alfa) entiendo la impedancia del sistema, es decir, la resistencia del sistema al flujo del proceso, y tau es la imagen del tiempo en las transformaciones de Laplace, como se vio después, y permite llevar el análisis del proceso desde el dominio diferencial al ordinario. Esto significa que cualquier proceso tiene su propio tiempo, distinto del nuestro, y tau actúa como un "traductor" de tiempos, si se me permite la expresión. En las entrañas del artículo di una forma de estimar tau:
Ahora bien, si se conocen los valores de la función f a los correspondientes instantes de tiempo t, entonces a partir de esta ecuación se determinan los parámetros n, τ y el coeficiente β de la siguiente manera:
donde:
Los valores de la función f a los correspondientes instantes de tiempo t y tiempo t vienen determinados por los valores reales del precio de mercado P0, P1,..., Pk a los instantes de tiempo h0, h1,..., һk desde el inicio de su desestabilización por diferenciación numérica, referida a la mitad del intervalo:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); y así sucesivamente;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; etc.