No consigo atravesar el laberinto de código, pero me gustaría compararlo.
Presupuesto inicial
Tenemos las siguientes variantes de alisado:
Resultado del suavizado
Ecuación de regresión:
eurusd = c(1)*eurusdsm(-1) + c(2)*tendencia + c(3)
Estimación de la ecuación de regresión
| Variable | Coeficiente | Stand.osh. | t-statistic | probabilidad |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
R-cuadrado = 0,788273
Error típico de la regresión = 0,015172
De las cifras obtenidas se desprende que
todos los coeficientes de regresión son significativos (la probabilidad de que sean iguales a cero es igual a cero)
la R-cuadrado es bastante alta (pero no muy alta), lo que significa que la regresión explica el 78% de la varianza
el error estándar es de 151 puntos. Es una cifra enorme.
¿Podemos fiarnos de las cifras resultantes?
Yo no lo haría, ya que según Jarque-Bera la probabilidad de que la serie suavizada tenga una distribución normal es del 31%.
Hagamos una previsión:
El error de previsión no está muy lejos del error de regresión y supera los 100 pips
Veamos el gráfico del error de previsión:
Bien, esto es un completo acabose: el error es variable, lo que significa que ¡el comportamiento futuro de la previsión es desconocido!
Para averiguar la razón, observemos la correlación de los coeficientes de la ecuación de regresión:
Podemos considerar que los coeficientes c(1) y c(3) están correlacionados casi al 100%.
Mi conclusión es que no podemos utilizar el suavizado exponencial para la predicción.
¿Por qué tenemos resultados diferentes?
Para mí es obvio que los parámetros óptimos que has encontrado no son más que un ajuste trivial. La regresión en sí no tiene remedio, sus coeficientes están correlacionados.
Para mí es obvio que los parámetros óptimos que has encontrado no son más que un ajuste trivial. La regresión en sí no tiene remedio, los coeficientes en ella están correlacionados.
Gracias por su interés en el artículo.
Por favor, aclare lo que quiere decir. ¿Qué resultados no convergen y cuáles son los parámetros óptimos?
Por favor, acláreme qué quiere decir con eso.
Perdona, dices que se puede usar, pero mi conclusión es que no.
¿Qué utilizar y por qué?
En conclusión, cabe señalar que los modelos de alisamiento exponencial son capaces, en determinados casos, de proporcionar previsiones tan precisas como las obtenidas con modelos más complejos, lo que confirma una vez más el hecho de que el modelo más complejo no siempre es el mejor.
Mi conclusión es que el alisamiento exponencial no debería utilizarse para hacer previsiones.
¿De qué tratan sus preguntas y por qué las hace?
Mi conclusión es que no se puede utilizar el suavizado exponencial para hacer previsiones.
¿De qué tratan tus preguntas y para qué sirven?
Me encantaría intentar responder a algo, pero necesito conocer la pregunta al menos. De lo contrario, tendré que adivinar y fantasear.
Intentaré aclararlo de nuevo.
Los modelos de suavización exponencial no se pueden utilizar para pronosticar el par eurusd, ¿alguna cita o nunca?
P.D..
Tienes en tu texto: "Ecuación de regresión:eurusd = c(1)*eurusdsm(-1) + c(2)*tendencia + c(3)". ¿Por qué regresión, el artículo es sobre modelos de alisamiento exponencial, y hay un modelo diferente, en lugar de c(3) hay una variable aleatoria con cierta distribución y dispersión?
En su texto: "Ecuación de regresión:eurusd = c(1)*eurusdsm(-1) + c(2)*tendencia + c(3)". ¿Por qué regresión, el artículo es sobre modelos de alisamiento exponencial, y hay un modelo diferente, allí en lugar de c(3) es una variable aleatoria con alguna distribución y varianza?
No funciona, hablando ciego con sordo. Vamos a posponerlo.
Enhorabuena de nuevo por un buen artículo.
No funciona, hablar de ciego a sordo. Pospongámoslo.
Enhorabuena de nuevo por un buen artículo.
La verdad es que tengo mucha curiosidad por conocer tu punto de vista sobre la previsión mediante alisado exponencial. Hay muchas cosas que no sé y siempre me alegra intentar descubrir algo nuevo en cada oportunidad, por eso hago preguntas.
Si no es mucha molestia, explíqueme por qué si la distribución de la secuencia original (o de la secuencia original suavizada) no es normal, no se puede confiar en la previsión. ¿O le he entendido mal?
Gracias por las felicitaciones.
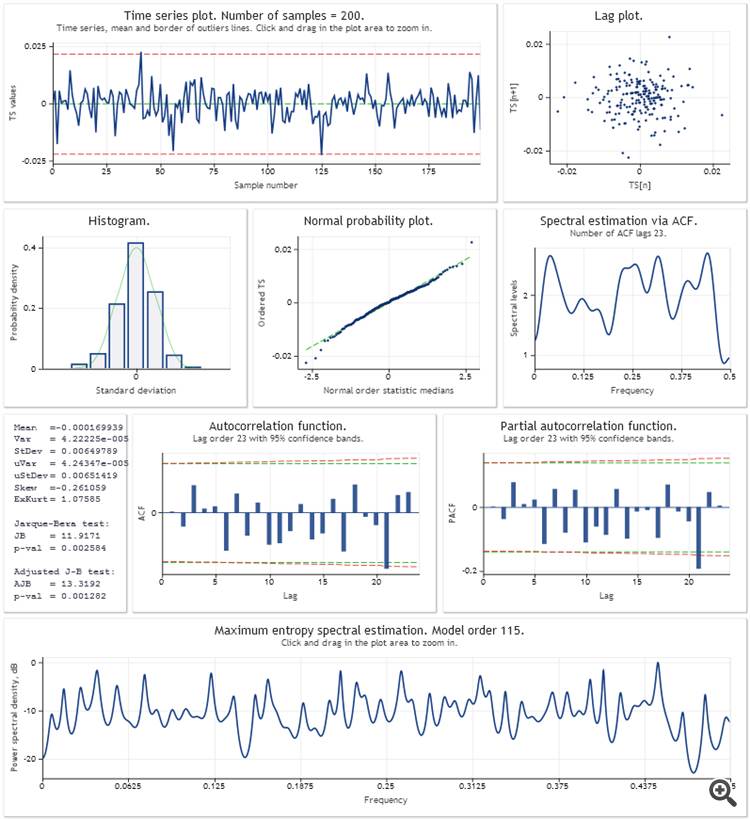
A continuación se presenta un análisis del error de predicción de un paso adelante para el modelo de crecimiento lineal aditivo con amortiguación. Los parámetros del modelo se optimizaron utilizando una muestra de los últimos 200 valores de USDJPY,M1. De la misma forma que en el script Optimisation_Test.mq5 del artículo.
https:// www.mql5.com/ru/articles/292
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Predicción de series de tiempo usando el ajuste exponencial:
Este artículo familiariza al lector con los modelos de ajuste exponencial utilizados en la predicción a corto plazo de series de tiempo. Además, toca los temas relacionados con la optimización y estimación de los resultados de las predicciones y proporciona algunos ejemplos de scripts e indicadores. Este artículo será útil como primera toma de contacto con los principios de la predicción basados en los modelos de ajuste exponencial.
Autor: Victor